Simulink混合系统模型：建模与仿真技术

一、混合系统的数学描述

混合系统是由不同类型的系统共同构成的，因此混合系统的数学描述可以由不同类型系统描述共同构成。但是由于混合系统的复杂性，一般难以用单独的数学模型进行描述或表达，因此混合系统一般都是由系统各部分输入与输出间的数学方程所共同描述的，下面举例说明。

对于如下的一个混合系统：设系统的输入为一离散变量，系统由离散系统与连续系统串联构成，其中离散系统输出经过一个零阶保持器后作为连续系统的输入。其中离散系统的输入输出方程为且系统采样时间为Ts=1s。

连续系统的输入输出方程为：

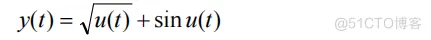
由于此混合系统中离散系统的输出经过一零阶保持器后作为连续系统的输入，因此数学关系为：

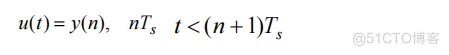
其中Ts=1s为离散系统的采样时间。故此混合系统的输入与输出之间的关系可以由下面的方程来描述：

二、混合系统的Simulink描述与简单分析

在对单独离散系统或连续系统进行描述时，由于系统一般比较简单，因而可以采用诸如差分方程、传递函数、状态空间等模型表示。但对于混合系统，由于系统本身的复杂性，即使是很简单的混合系统，如上面给出的例子，都难以用一个简单的模型进行描述。因此，这里采用简单的数学方式对系统进行描述与分析。

编写M脚本文件，对上面中的混合系统进行分析。

登录后复制

clc
close all
clear
t=1:0.1:99.9; %表示在时间[1，99.9]范围内分析系统。时间间隔0.1 s
n=1:100; %表示系统输入时刻为1~100 s
un=0.5*n; %表示系统输入u(n)
yn=un+1; %表示系统中离散部分的输出，即连续部分的输入
for i=1:length(n)-1
    for j=1:length(t)
        if t(j)>=n(i) && t(j)<n(i+1) %判断连续部分的输入时间范围
            y(j)=sqrt(yn(n(i)))+sin(yn(n(i))); %计算系统输出
        end
    end
end
figure
plot(t,y);
grid; %绘制系统输出曲线图系统输出曲线

从系统输出曲线图中可以看出：由于系统中离散部分的输出经过零阶保持器后作为连续部分的输入，而零阶保持器具有阶跃的特性，在系统仿真结果中出现阶跃现象。另外，系统呈现类似正弦发散的特征表明系统为一发散不稳定系统。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删