FPGA浮点单元设计与优化

浮点数在内存中的存放格式例如以下：

地址        +0          +1           +2           +3
内容    SEEE EEEE   EMMM MMMM    MMMM MMMM    MMMM MMMM

这里
S 代表符号位，1是负，0是正
E 偏移127的幂。二进制阶码=(EEEEEEEE)-127。
M 24位的尾数保存在23位中，仅仅存储23位。最高位固定为1。此方法用最较少的位数实现了
较高的有效位数。提高了精度。

零是一个特定值，幂是0 尾数也是0。

浮点数-12.5作为一个十六进制数0xC1480000保存在存储区中，这个值例如以下：
地址 +0     +1     +2     +3
内容0xC1   0x48   0x00   0x00

浮点数和十六进制等效保存值之间的转换相当简单。

以下的样例说明上面的值-12.5怎样转
换。

浮点保存值不是一个直接的格式。要转换为一个浮点数，位必须按上面的浮点数保存格式表
所列的那样分开。比如：

地址       +0           +1            +2            +3
格式   SEEE EEEE    EMMM MMMM     MMMM MMMM     MMMM MMMM
二进制  11000001     01001000      00000000      00000000
十六进制   C1           48            00            00

从这个样例能够得到以下的信息：
 符号位是1 表示一个负数
 幂是二进制10000010或十进制130。130减去127是3。就是实际的幂。
 尾数是后面的二进制数10010000000000000000000

在尾数的左边有一个省略的小数点和1,这个1在浮点数的保存中常常省略,加上一个1和小数
点到尾数的开头,得到尾数值例如以下:
1.10010000000000000000000

接着,依据指数调整尾数.一个负的指数向左移动小数点.一个正的指数向右移动小数点.由于
指数是3,尾数调整例如以下:
1100.10000000000000000000

结果是一个二进制浮点数，小数点左边的二进制数代表所处位置的2的幂。比如：1100表示
(1*2^3)+(1*2^2)+(0*2^1)+(0*2^0)=12。
小数点的右边也代表所处位置的2的幂，仅仅是幂是负的。比如：.100...表示(1*2^(-1))+
(0*2^(-2))+(0*2^(-2))...=0.5。

这些值的和是12.5。由于设置的符号位表示这数是负的，因此十六进制值0xC1480000表示-
12.5。

FPGA流水线形式的浮点单元例如以下所看到的：

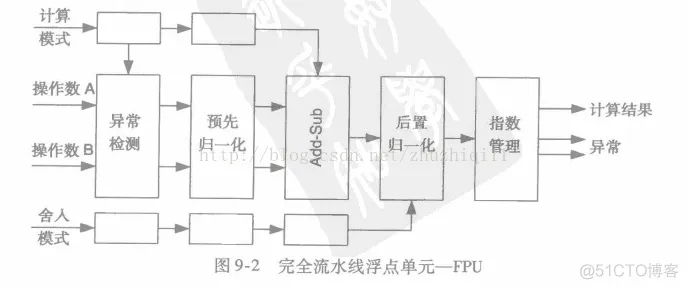
第一步：检測是否在异常区域（指数为零）。处在正常区则加入逻辑1到尾数的最高位（即把尾数的位变成24），否则加入零。

按此原理那么数据越大小数位的精度也就越低。

第二步：两个数中较小的数必须进行调整，使得尾数的指数相等。由于大数的小数位占的少，因此要舍去小数的尾数，使得数据之间指数对齐。即归一化，向右移两个指数的差值就可以。

第三步：符号检測并进行加减操作，然后在进行归一化处理。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删