COMSOL软件应用：高效计算平均曲率的方法

笛卡尔坐标下平均曲率表达式可以简写成：

网格的单位法向量 N = (n1,n2,n3)，在COMSOL中分别为 (nx,ny,nz)

因此理论上COMSOL计算曲率方程为 kappa = nxx+nyy+nzz。

但是由于软件没有对  nx ny nz进行进一步差分，所以需要引入辅助变量来计算 nxx nyy nzz。

以2D为例：

使用 Weak Form Boundary PDE模块 选择需要计算的曲线，定义变量 norm1, norm2.

方程中填入：

定义边界辅助变量 kappa = norm1Tx+norm2Ty


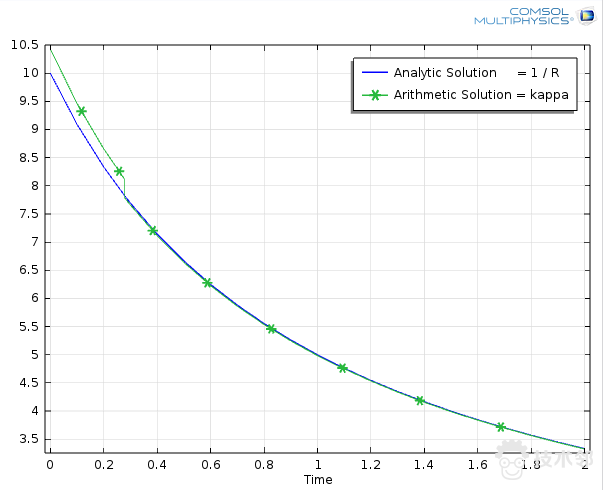
比如计算一个扩张的圆的曲率，理论曲率 为 1/R：

其曲率变化，使用了自适应网格，数值略有跳跃，但吻合度还是不错的：

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删