NX Nastran单元库进阶：2D Elements理论深化

面单元，也称2D单元，用于描述那些厚度方向的尺寸与其他方向的尺寸相比很小的结构。你可以用面单元来表达平板、单曲率壳（如圆柱面）或双曲率壳（如球面）。板单元的节点具有五个自由度，缺少垂直于单元转动的自由度。应该约束这个方向的转动自由度，避免刚度矩阵奇异。

在 NX Nastran中，你可以使用以下类型的2D单元：

•Shear panel (CSHEAR) 剪切面板

•2D crack tip element (CRAC2D) 2D裂纹末梢单元

•Conical shell (RINGAX) 锥形壳

•Shell (CQUAD4, CTRIA3, CQUAD8, CTRIA6, CQUADR, CTRIAR) 壳 对于线性分析，NX Nastran 假定板壳单元符合薄板特性的经典假设（Kirchhoff假定）：

•薄板厚度远远小于宽度或长度尺寸。

•中面的变形较其厚度而言非常小。

•在弯曲过程中，中面不产生应变（中性面）- 这适用于横向载荷，但不适用于面内载荷。

•中面的法线在弯曲过程始终保持与中面垂直。（直法线假定：弯曲变形前垂直于中面的直线段，变形后仍为直线且长度不变）补充板壳力学基础理论

学习板壳力学之前，首先要了解弹性力学的三大基本方程。

几何方程

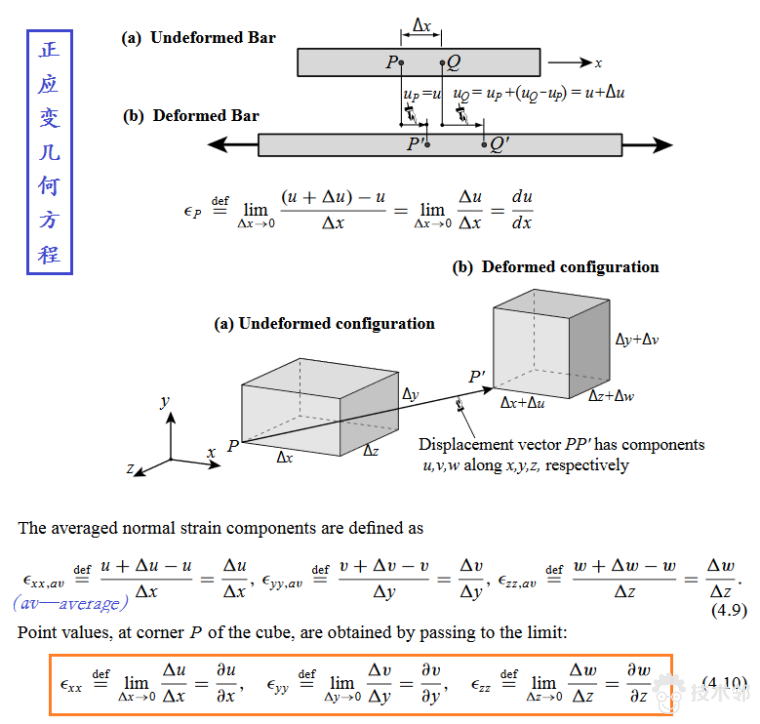
物理方程（广义胡克定律）

平衡方程

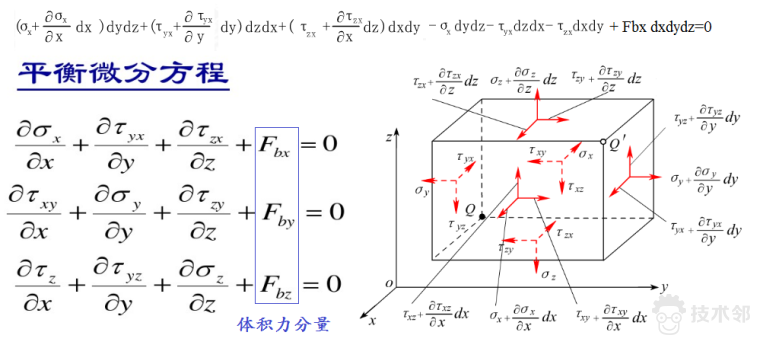
1、薄板小挠度弯曲基本假定：除了满足弹性力学中均匀性、连续性、各向同性、完全弹性、小变形外，还增加以下三个计算假定（Kirchhoff假定）。 （1）假定垂直于中面方向的应变可以忽略不计。即有

（2）假定应力分量、、， 远小于其余三个应力分量，它们引起的应变可以忽略不计。即有

（3）假定薄板中面内的各点都没有平行于中面的位移。即z=0时，x方向位移u=0、y方向位移v=0。

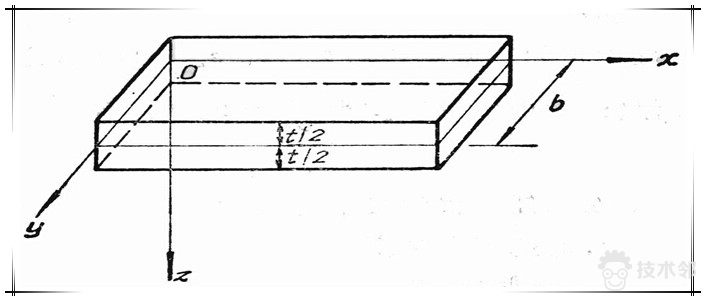
纵向载荷：设认为沿薄板厚度均匀分布，按平面应力问题处理。

横向载荷：使薄板弯曲，它们引起的应力、应变和位移按薄板弯曲问题计算。

Kxx、Kyy 分别是变形后中面上任意点处zx平面和zy平面上的曲率，Kxy 表示扭率。

这样就得到了挠度w(x,y)的微分方程。

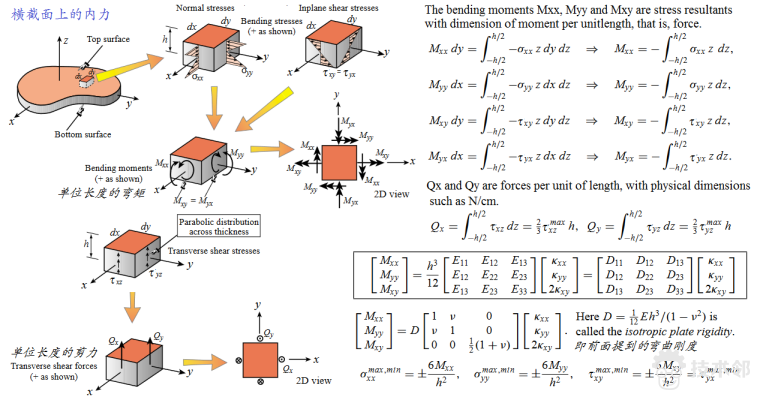
通过以上理论分析，我们得到了薄板弯曲问题的挠度微分方程和应力计算公式。 这里我用NASTRAN做了一个简单的薄板弯曲的实例，进行验证。

长度L=100mm，宽度w=20mm，厚度t=1mm。

理论计算σxx正应力的最大值

x坐标长度方向的均布载荷：q=0.01*20=0.2N/mm

剪力图、弯矩图：

最大弯矩：M=q*L^2/8=0.2*10000/8=250Nmm

x方向最大的单位长度弯矩：Mxx=M/w=250/20=12.5N

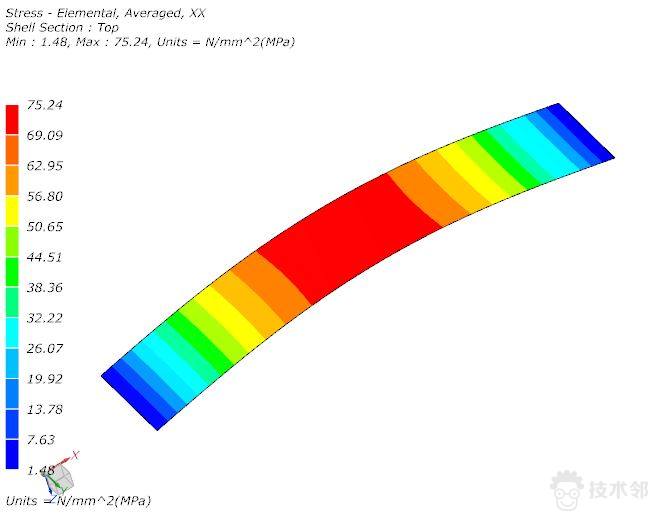
x方向最大正应力：σxx=6*M/t^2=6*12.5=75MPa

仿真得到的应力结果与之相符。

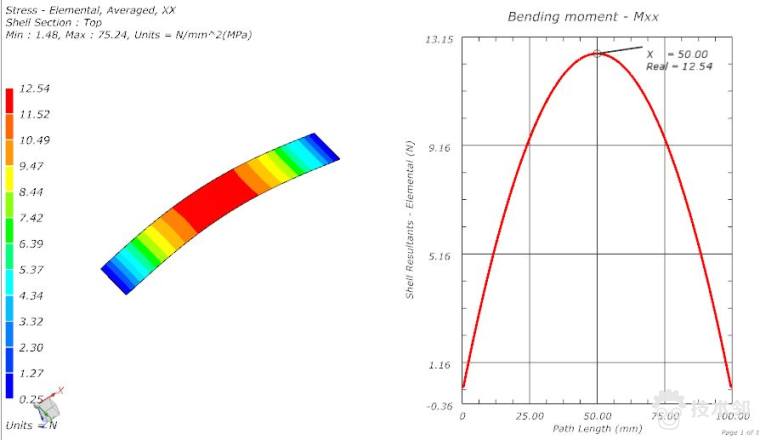
x方向单位长度的弯矩Mxx的分布如下。中间位置弯矩最大，Mxx=12.5，乘以宽度20，正好是最大弯矩250Nmm，与理论分析的弯矩图相符。

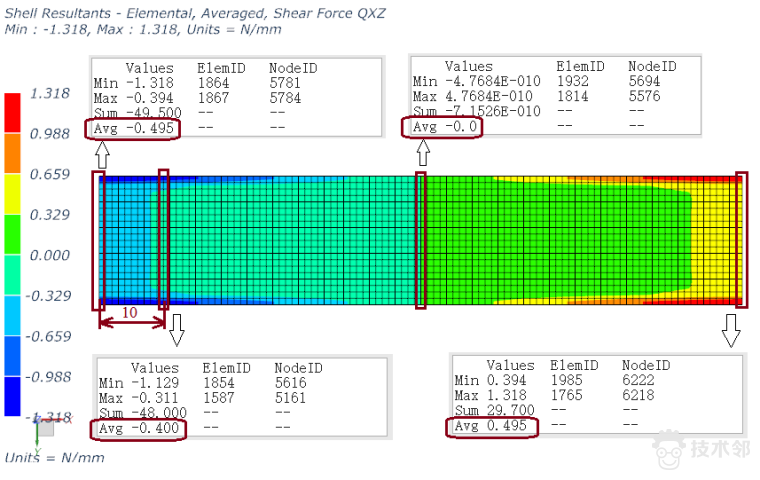
x方向截面上的单位长度剪力Qxz分布如下，检查每个截面上的平均值：两端是±0.5，中间是0，距离一端10mm处是0.4，分别乘以宽度20，与剪力图相符。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删