==概述==
本系列文章研究成熟的有限元理论基础及在商用有限元软件的实现方式。有限元的理论发展了几十年已经相当成熟,商用有限元软件同样也是采用这些成熟的有限元理论,只是在实际应用过程中,商用CAE软件在传统的理论基础上会做相应的修正以解决工程中遇到的不同问题,且各家软件的修正方法都不一样,每个主流商用软件手册中都会注明各个单元的理论采用了哪种理论公式,但都只是提一下用什么方法修正,很多没有具体的实现公式。商用软件对外就是一个黑盒子,除了开发人员,使用人员只能在黑盒子外猜测内部实现方式。


一方面我们查阅各个主流商用软件的理论手册并通过进行大量的资料查阅猜测内部修正方法,另一方面我们自己编程实现结构有限元求解器,通过自研求解器和商软的结果比较来验证我们的猜测,如同管中窥豹一般来研究的修正方法,从而猜测商用有限元软件的内部计算方法。我们关注CAE中的结构有限元,所以主要选择了商用结构有限元软件中文档相对较完备的Abaqus来研究内部实现方式,同时对某些问题也会涉及其它的Nastran/Ansys等商软。为了理解方便有很多问题在数学上其实并不严谨,同时由于水平有限可能有许多的理论错误,欢迎交流讨论,也期待有更多的合作机会。
==几何梁单元的刚度矩阵的研究==
一般商用软件的梁都有两类:
1) 一类是已知截面属性参数的梁,即General梁(也叫参数梁),在Abaqus中创建梁时选择General就是General梁。
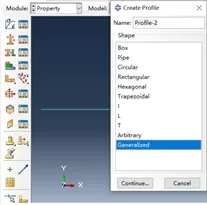
2) 另一类是已知截面形状类型和几何尺寸的梁,即Geometry梁(也叫几何梁),在Abaqus创建梁截面时选择除General外的其它选项都是Geometry梁。


实际的梁都是有截面形状的,也就是几何Geometry梁,商用软件分析时都采用两步走的形式:
1) 第一步:通过这些截面形状类型和参数得到构建梁单元所需的基本截面属性参数,譬如矩形面积=长*宽等。
2) 第二步:利用上面得到的截面属性参数组成梁单元的刚度矩阵。
梁相对壳来说,商业软件的修正方式相对较少,如果自己编程序,采用这些修正方式可以得到和商业软件完全一致的梁单元刚度矩阵,如果刚度矩阵完全一致,那么对任何的梁的算例都可以得到和商业软件完全一致的结果了。在本系列第六篇我们讨论了General梁单元的刚度矩阵的基本理论和Abaqus的修正方式,Geometry梁的计算方法只是比第一类梁多了一步怎么从截面几何参数得到截面属性参数,当然针对不同形状类型,Abaqus计算截面属性参数时也做了许多的修正,本篇中将进行讨论。然后在自编有限元程序iSolver实现同样的修正方式,最后验证iSolver的结果和Abaqus完全一致,从而证明Abaqus对几何梁的内部修正和我们设想的一致。同时,通过L梁的算例将会证明Abaqus用户手册的一点小错误(难得发现Abaqus文档的错误^.^),即General梁的惯性矩后台计算时是相对于形心的(而不是文档所说的相对于1-2轴的)。具体验证过程也可以参考我们的演示录像。
==总结==
本文研究了Abaqus中几何梁的B31单元的刚度矩阵的求解方式,以L梁为例,介绍General梁用到的面积、惯性矩、扭转常数等参数在几何梁中是如何通过几何形状求得的,根据这些参数,可以得到和Abaqus完全一致的刚度矩阵,从而对只有几何梁组成的任意模型一般都能得到Abaqus完全一致的分析结果,并用一个简单的算例验证了该想法。
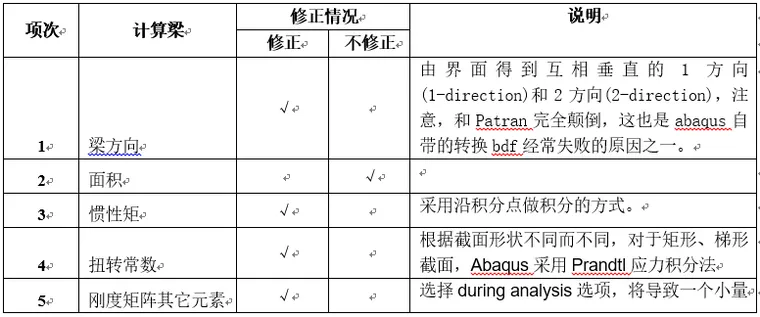
从一个几何梁到General梁的转化,需要计算的量和Abaqus的修正情况如下:
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删