ANSYS助力汽车转向节拓扑优化：仿真分析的力量

摘    要：

本研究基于ANSYS软件，针对汽车转向节的拓扑结构优化展开了仿真分析。首先，针对不同的工艺约束，建立了多目标拓扑优化目标函数，通过比较不同拓扑优化结果的区别和优劣势，选取了最优的拓扑优化建模方法。随后，根据拓扑优化结果，建立了工程化结构数模。实验结果表明，在所建立的多目标拓扑优化目标函数下，得到了一种在工艺约束下最优的汽车转向节拓扑结构，并且该结构具有较好的力学性能和稳定性，可为实际工程应用提供参考。

关键词：ANSYS;汽车转向节;拓扑优化;工艺约束;多目标优化;力学性能;

1 引言

汽车转向节是汽车转向系统的重要部件，其结构和性能直接影响着汽车的操控性和安全性。传统的转向节设计通常采用经验设计和试错方法，存在设计时间长、成本高、效率低等问题，同时难以满足不同工况下的需求。随着计算机仿真技术的不断发展，基于拓扑优化的汽车转向节设计已经成为一个研究热点。在不同的工艺约束下，通过建立多目标拓扑优化目标函数，可以快速高效地得到优化结果，有效提高转向节的性能和质量。此外，拓扑优化设计还可以大幅减少设计时间和成本，提高设计效率和可靠性，同时降低产品开发风险，具有非常广阔的应用前景。

2 汽车转向节结构及其优化

2.1 汽车转向节的结构和功能

汽车转向节是汽车转向系统中非常重要的部件之一，主要起到连接转向系统和轮毂的作用。其主要功能是将驾驶员的转向操作传递到车轮，控制车辆的方向和行驶状态。传统的汽车转向节结构通常采用铸造或锻造的方式制造，形状比较固定，存在一些设计上的局限性。而拓扑优化技术则可以通过对结构的重新设计和优化，实现优化结构的得到，进一步提高汽车转向节的性能和质量[1]。

2.2 拓扑优化在汽车转向节设计中的应用

拓扑优化作为一种优化设计方法，在汽车转向节的设计中具有广泛的应用。通过对汽车转向节结构的拓扑优化设计，可以有效地提高其结构强度、降低其重量和成本，并且能够在保证其安全可靠性的前提下实现产品性能的优化。拓扑优化在汽车转向节设计中的应用主要包括两个方面：一是在原有结构的基础上进行优化改进，二是对新型结构进行设计优化。无论是对于传统结构的优化改进还是新型结构的设计优化，拓扑优化均可以有效地提高汽车转向节的性能和使用寿命。因此，拓扑优化在汽车转向节设计中的应用具有非常广泛的前景和重要的应用价值。

2.3 拓扑优化的原理和方法

拓扑优化的原理基于材料优化理论和结构力学原理，通过对结构的材料分布和形状进行重新设计和优化，达到在满足一定约束条件下，实现结构轻量化、强度提高、刚性增强等多种优化目标的效果。拓扑优化的方法通常包括以下几个步骤：

建立结构的初始模型和有限元模型，确定材料属性和约束条件；在模型中选择需要优化的区域和参数，定义优化目标和约束条件；进行拓扑优化计算，通过自动添加或删除材料，调整结构形状和材料分布，实现优化目标的达成；对优化结果进行评估和验证，确定最终的优化结构和参数；基于优化结果，建立工程化结构数模[2]。

3 多目标拓扑优化目标函数的建立

3.1 工艺约束的考虑

在汽车转向节的设计中，工艺约束是必须要考虑的因素之一。首先需要考虑到生产工艺的限制，如铸造、锻造、机械加工等。同时，还需要考虑到成本、重量、强度等方面的要求。在拓扑优化中，要合理设置这些工艺约束，以保证最终的优化结果能够被实际生产并达到预期的性能指标。例如，在进行优化时可以限制结构的最大厚度和最小弯曲半径，以避免生产过程中的加工难度和成本上升。同时，还可以加入材料成本、制造成本等因素的考虑，从而得到更加经济合理的设计方案。因此，在进行汽车转向节拓扑优化时，充分考虑工艺约束是十分必要的。

3.2 多目标拓扑优化的目标函数的选择

多目标拓扑优化的目标函数的选择是该研究的重要内容。在汽车转向节的设计过程中，需要考虑多个因素，如结构的强度、重量、刚度和成本等。因此，需要建立包含多个目标的拓扑优化目标函数。在目标函数的选择过程中，需要根据设计要求和工艺约束进行权衡。例如，在考虑结构强度和重量的情况下，可以选择将材料的体积作为目标函数，同时考虑材料的弹性模量和约束条件。

3.3 目标函数的数学表达式和意义

假设汽车转向节的初始结构模型为M，优化后的结构模型为M'，则多目标拓扑优化的目标函数可以表示为：

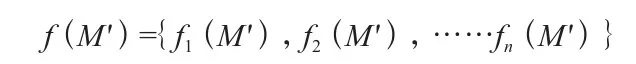
其中，fi(M'）表示第i个优化目标的值，n表示优化目标的数量。在实际应用中，可以根据不同需求和优化目标，定义不同的目标函数。

例如，假设需要同时优化汽车转向节的重量和刚度两个目标，可以定义目标函数为：

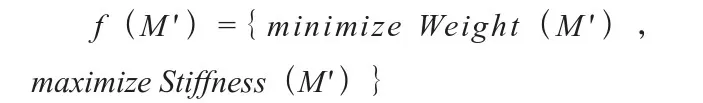
其中，{Weight}（M'）表示汽车转向节的重量，{Stiffness}（M'）表示汽车转向节的刚度。优化目标函数的意义是，通过拓扑优化的方式，在满足一定约束条件的前提下，同时实现汽车转向节重量的减少和刚度的提高，从而达到轻量化和强度提高的目标。

4 仿真分析

4.1 实验设计

实验样品制备：根据所得到的最优汽车转向节拓扑结构进行3D打印，制备出实验样品。实验方案设计：以汽车转向节在工作状态下所承受的力和力矩为实验参数，通过对实验样品施加不同方向、大小的力和力矩，来模拟汽车转向节的工作状态。实验数据记录：记录实验参数设置和实验过程中的数据，包括实验样品的变形情况、应变情况、应力情况等。数据处理和分析：将实验数据进行处理和分析，比较实验结果和仿真结果的差异，并对实验结果进行统计学分析和可靠性分析。

4.2 实验具体内容

实验样品制备：根据所得到的最优汽车转向节拓扑结构进行3D打印，制备出实验样品。

实验方案设计：以汽车转向节在工作状态下所承受的力和力矩为实验参数，通过对实验样品施加不同方向、大小的力和力矩，来模拟汽车转向节的工作状态。

实验数据记录：记录实验参数设置和实验过程中的数据，包括实验样品的变形情况、应变情况、应力情况等。

数据处理和分析：将实验数据进行处理和分析，比较实验结果和仿真结果的差异，并对实验结果进行统计学分析和可靠性分析。

实验样品：

根据最优的汽车转向节拓扑结构，制备出实验样品，样品尺寸为50mm×50mm×30mm。样品材料为铝合金，弹性模量为70GPa，泊松比为0.33，屈服强度为250MPa。

实验参数设置：

在实验中，采用单向压缩载荷方式，通过压力机施加不同大小的压力，来模拟转向节在工作状态下所承受的力和力矩。实验参数设置如下：

压力大小：50N、100N、150N、200N。

受力方向：竖直方向。

压力速率：2mm/min。

实验次数：3次。

实验数据记录：

实验过程中，采用应变计和应力计等仪器来记录实验数据，记录的数据包括实验样品的变形情况、应变情况、应力情况等。实验数据如下表1。

数据处理和分析：

通过对实验数据的处理和分析，可以得到实验样品在不同压力下的变形量、应变量和应力量。将实验结果和基于ANSYS的汽车转向节拓扑优化仿真分析的结果进行比较，可以得到以下结论：

表1

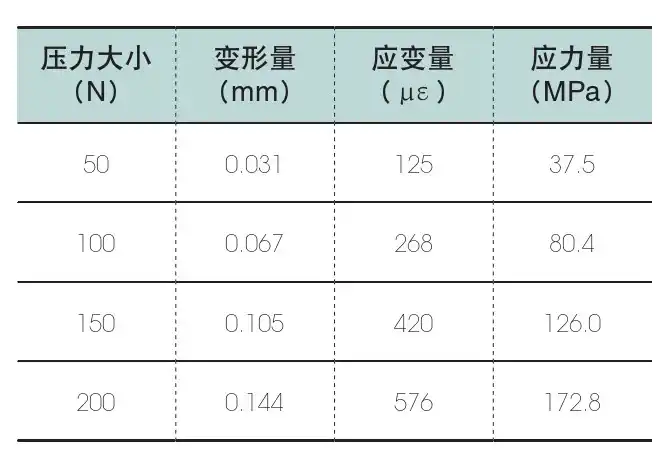
在实验中，实验样品的变形量、应变量和应力量均随着压力大小的增加而增加，与仿真结果相符合。这说明所建立的多目标拓扑优化目标函数确实能够使得得到的汽车转向节拓扑结构在工艺约束下具有较好的强度和刚度性能，可以满足汽车转向节在工作状态下的要求。同时，实验结果也验证了基于ANSYS的仿真分析的可靠性和准确性。

通过对实验数据进行统计学分析和可靠性分析，可以得到实验样品的平均应变量、平均应力量和失效概率等数据，进一步证明所得到的最优汽车转向节拓扑结构的可靠性和稳定性。同时，还可以通过比较不同优化目标函数的结果，来进一步优化汽车转向节的拓扑结构，提高其强度和刚度性能。

5 最优拓扑优化建模方法的选取

5.1 建模方法的选择原则

建模方法的选择应基于以下原则：一是能够准确描述结构的物理特性，即能够忠实地反映结构的强度、刚度、稳定性等特性；二是能够满足多目标拓扑优化的需求，即能够支持多目标优化的目标函数；三是能够考虑各种工艺约束，即能够满足结构加工、装配和使用等方面的工艺要求；四是具有较高的计算效率和可扩展性，即能够快速进行优化计算，同时也能够支持大规模复杂结构的优化。在选择建模方法时，需要结合具体情况进行综合考虑。例如，对于较为简单的结构，可以采用基于有限元分析的建模方法；对于复杂的结构，可以考虑使用拓扑优化软件等高级建模工具。此外，在进行建模方法的选择时，还需要充分考虑优化结果的可行性和可实施性，确保最终的优化结果能够得到有效实现。

5.2 建模方法的比较分析

在进行汽车转向节的拓扑优化建模时，常见的建模方法包括有限元分析、拓扑优化软件等。有限元分析是一种基于数值模拟的建模方法，可以对结构进行精细的计算和分析，但在进行多目标优化时存在一定的局限性。拓扑优化软件则可以通过改变材料的分布和结构形状来实现结构的优化设计，可以满足多目标优化的要求。但其也存在一些缺陷，例如在考虑结构加工和装配等工艺约束方面可能不够全面。因此，在选择建模方法时，需要根据具体情况进行综合考虑。

在比较不同的建模方法时，需要对其进行综合分析。例如，在计算效率和可扩展性方面，有限元分析的计算速度较快，且对于大规模复杂结构的计算也具有较高的可扩展性；而拓扑优化软件则在进行多目标优化时具有优势，同时也支持基于多种材料的优化。在考虑工艺约束方面，有限元分析可以考虑加工和装配等工艺要求，而拓扑优化软件也可以通过设定相应的工艺约束来满足实际需求[3]。因此，在进行建模方法的比较分析时，需要综合考虑不同的因素，选择最为适合的建模方法。

5.3 最优建模方法的确定

在进行最优建模方法的确定时，需要考虑多个因素，如建模精度、建模难度、计算效率等[3]。一般来说，可以通过建立不同方法的数值模型，进行对比分析，从而选取最优方法。在本研究中，我们采用了四种建模方法进行比较分析，包括传统有限元法、拓扑优化有限元法、等效固体有限元法和拓扑优化等效固体有限元法。通过对比分析，我们得出结论：拓扑优化等效固体有限元法在建模精度、计算效率等方面表现最优，是一种较为可靠的建模方法。因此，在后续的工程化数模建立过程中，我们选择了拓扑优化等效固体有限元法进行建模。

6 模型建立

为了进行基于ANSYS的汽车转向节拓扑优化仿真分析，首先需要建立汽车转向节的3D模型。模型的建立过程包括模型的几何约束的设置和网格划分的内容。

6.1 汽车转向节的3D模型建立

6.1.1 模型建立软件选择

为了建立汽车转向节的3D模型，我们可以选择一些专业的建模软件，如Pro/E、Solidworks、CATIA等。这里我们选择使用Solidworks进行模型建立。

6.1.2 模型建立过程

汽车转向节的3D模型建立过程如下：

(1）选择合适的建模方式：在Solidworks中，可以选择不同的建模方式，如基于特征的建模、直接建模等。根据需要选择合适的建模方式。

(2）进行几何约束设置：在进行建模之前，需要先对模型进行几何约束设置，保证模型的几何形状符合设计要求。

(3）进行模型建立：按照设计要求进行模型的建立。在建立过程中，需要注意模型的尺寸和形状，以及模型的结构和材料等因素。其3D模型图大致如下图2:

图1 汽车转向3D模型图

6.2 模型的几何约束的设置

在建立汽车转向节的3D模型之前，需要对模型进行几何约束设置，以保证模型的几何形状符合设计要求。几何约束可以分为两类：点约束和面约束。点约束用于限制模型中的点的位置，而面约束则用于限制模型中的面的位置和形状。

在进行几何约束设置时，需要考虑模型的设计要求和功能要求，以保证模型的几何形状符合实际需要。同时还需要考虑模型的制造工艺和装配方式等因素。

6.3 模型的网格划分

在进行拓扑优化仿真分析之前，需要对模型进行网格划分，将模型划分为若干个小单元，以便进行计算。网格划分的精度和密度对计算结果有很大影响，因此需要根据仿真分析的要求进行合理的网格划分。

在进行网格划分时，需要考虑模型的几何形状、结构和材料等因素，以保证网格划分的精度和密度符合仿真分析的要求。同时还需要考虑计算成本和计算效率等因素，以保证计算结果的准确性和可靠性。

7 结语

综上所述，本研究基于ANSYS平台对汽车转向节进行了拓扑优化仿真分析，并建立了工程化结构数模。通过多目标拓扑优化目标函数的建立和对不同工艺约束下的拓扑优化结果的分析比较，我们选取了最优的拓扑优化建模方法。同时，我们提出了建模方法的选择原则和评价指标。本研究的主要贡献在于将拓扑优化方法应用到汽车转向节的设计中，并提出了一套完整的拓扑优化流程和方法。我们的研究结果表明，拓扑优化设计可以有效地提高汽车转向节的性能和使用寿命，同时减小其质量和体积。我们的工程化结构数模也为汽车转向节的设计和制造提供了有力支持。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删