概述

对于以单元为中心的 CFD 流动求解器，使用连通性信息在重叠域中进行插值通常会使用最小二乘法来确定插值权重。使用最小二乘法产生的权重不受 0 和 1 之间的限制。因此，插值可能是非单调的，并且会在解中引入新的极值，这会给 CFD 解带来困难。使用连接原始单元中心以形成双网格单元的双网格插值可以与三线性插值一起使用以产生介于 0 和 1 之间的权重。全局的双网格方法，其中单个网格连接所有单元格中心，其存储成本可能很高。在使用一组局部对偶网格时，其中每个原始网格元素都有一个独立于相邻局部对偶的关联局部对偶网格，可以通过仅加载插值所需的局部双网格集来减少内存需求。在本文中，将使用最小二乘插值权重的可压缩 CFD 解决方案与使用全局双网格插值权重的解决方案进行了比较。这些结果表明，使用最小二乘插值权重的非单调插值会导致解不稳定。当使用双网格插值权重时，观察到 CFD 解更稳定。这些结果表明，使用最小二乘插值权重的非单调插值会导致解不稳定。当使用双网格插值权重时，观察到 CFD 解更稳定。这些结果表明，使用最小二乘插值权重的非单调插值会导致解不稳定。当使用双网格插值权重时，观察到 CFD 解更稳定。

介绍

重叠或嵌合网格方法利用一组重叠网格来离散化解决方案域。组件网格可以在不考虑几何体其他部分的情况下进行拟合，并且可以在很大程度上简化网格生成过程。结果是一个灵活的计算模拟框架，可以在许多情况下成为推动力。它已被广泛用于简化复杂几何结构的结构化网格生成要求。使用重叠网格系统也是模拟相对运动物体的一种很有前途的解决方案，例如从飞机和旋翼飞机上掉落的油箱。

在确定重叠复合网格系统上的流动解决方案时，点模板和定义插值权重的方法是关键因素。这种插值的精度和平滑度会影响流解的精度和稳定性。网格中流相关变量的位置会影响插值模板和用于确定插值权重的方法。

双网格

原始网格由网格点组成，其中这些网格点之间的单元连接由网格生成软件生成。这组细胞类型通常是四面体、六面体、棱柱和金字塔。

双网格由原始网格的单元中心和这些双网格点的连通性组成，以形成双单元。必须定义双网格单元连接，因为我们只提供了原始网格单元连接。构建的双网格单元的类型将显着影响用于插值的方案。使用最小二乘法计算权重的一个缺点是权重不受 0 和 1 的限制。非结构化网格的双网格将提供与结构化网格相同的好处，但以更多的内存和时间为代价。

A. 结构化双网格

对于结构化网格，以单元为中心的位置之间的连接以与点/节点相同的方式隐含。由于双网格连接单元格中心，因此它们不会覆盖与节点或原始网格相同的体积。双网格单元不覆盖边界单元中心和网格边界之间的空间。因此，双网格中的供体必须对位于边界单元中心和块边界面之间的空隙中的任何边缘使用外推法。如果连接规则且拓扑一致，则双网格可以跨点匹配块到块接口扩展。

B. 非结构化双网格

图 1 显示了一个由三角形（黑线）和显示为蓝点的单元中心组成的非结构化原始网格。一种可能的带有三角形的双网格以浅蓝色显示，它连接单元格中心。三维中的非结构化单纯形双网格单元将是四面体。显然，需要多个双网格三角形来覆盖原始三角形。因此，必须通过双网格中的供体搜索来增强原始网格中的供体搜索，以找到正确的双供体细胞。

图 1. 以细胞为中心的非结构化原始网格和对偶网格。

C. 结构化双网格供体六面体

Suggar++ 软件中的供体搜索最初将在原始网格上运行，即使请求双网格供体也是如此。原始网格供体单元被用作双网格供体六面体的一个角，并且程序尝试使用适当的邻居来形成六面体的剩余角。由于双网格连接细胞中心，请注意，如果边缘落在细胞中心和边界面之间的体积中，则边缘位置将在双网格供体之外，并且会发生外推。

D. 减少双网格供体

如前所述，双网格不会覆盖与节点或原始网格相同的体积，并在边界附近留下空隙。位于此空隙中的边缘点将找到原始网格供体，但双网格供体将需要外推，可能导致非单调插值，内插值不受供体成员值的限制。

如果用户接受边界法线方向插值精度的降低，则可以保留单调插值。双网格供体成员可以减少为四边形，但当边界没有单一法线方向时，减少程序会将供体细胞减少为单个供体成员：原始细胞。类似的还原过程用于非结构化双网格，其中当边缘点位于边界面附近并且在双四面体网格之外时，供体将自动退化为三角形、线和点。

E. 以细胞为中心的供体使用双网格的好处

与默认的以细胞为中心的供体相比，以细胞为中心的双网格供体可以提供显着的好处。如前所述，默认以细胞为中心的供体的供体成员是供体细胞及其邻居，其中供体权重使用最小二乘法计算。这些最小二乘权重可能不受零和一的限制，并且可能导致非单调插值。此外，随着边缘位置从一个供体单元格移动到相邻单元格，内插值可能不连续，因为供体成员将发生变化。相反，双网格供体使用插值单元连接原始单元区域中的单元中心。

对于结构化网格，双网格供体将是连接供体细胞中心与相邻细胞中心的六面体。对于非结构化网格，单纯形双网格供体将是连接原始双细胞区域中的细胞中心的四面体。双网格四面体供体插值的好处必须与非结构化双网格的存储成本和双网格内的第二供体搜索进行权衡。双网格中的网格点将是原始网格的单元中心。对偶网格中四面体数量的估计将是原始网格中单元中心数量的 6-7 倍。因此，双网格存储可以相当大。

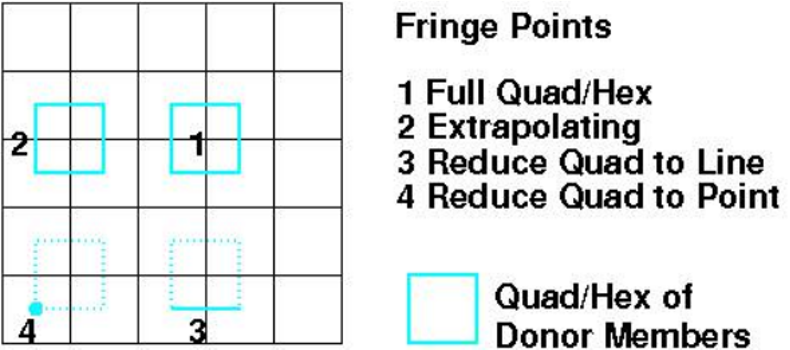
图 2. 边界附近有边缘的以细胞为中心的双网格供体。

双电网能力评估案例

在 RavenCFD 中选择了两种几何形状进行模拟，以评估 Suggar++ 中的双网格能力。第一个是高超音速 HIFiRE-1 圆锥/圆柱/耀斑几何形状，第二个是 NASA 通用研究导弹。选择这些几何形状是因为存在用于比较和评估一系列流态的实验数据。

A.HIFIRE-1

HIFiRE-1 是由高超音速国际飞行研究和实验 (HIFiRE-1) 飞行测试计划评估的高超音速圆锥/圆柱/耀斑几何形状。在目前的工作中，RavenCFD 模拟选择了壁温为 300 K 的马赫 7.16 情况，以三种形式进行，以评估双网格供体方法。

1. 无插值函数裁剪的最小二乘供体加权
2. 具有插值函数裁剪的最小二乘供体加权
3. 无插值函数裁剪的双网格供体加权

在这些情况下，插值区域被推到非常靠近 HIFiRE-1 主体的位置，以确保插值发生在高梯度区域。图 3 是沿 y 轴的切片，它显示了 HIFiRE-1 几何表面上的壁热传递行为和火炬区域中的整体流动行为，用于使用带插值函数裁剪的最小二乘加权进行模拟。

双网格需要更多的内存，但在这种情况下，总体供体搜索挂钟时间显示的差异很小。如前所述，最小二乘法有一个严重的缺点，即权重可能不受 0 和 1 的限制。因此，插值可能是非单调的，并且会在解中引入新的极值，从而给流求解器带来困难。这种行为在 RavenCFD 中模拟 HIFiRE-1 几何结构时得到了例证。

当使用没有裁剪的最小二乘供体加权时，插值函数导致数值困难，并且模拟崩溃。虽然使用具有限幅的插值函数的最小二乘施主加权的模拟进行到收敛。正如预期的那样，使用没有插值函数裁剪的双网格供体的模拟能够继续收敛。因此，双网格有效地限制了插值函数，以消除将错误极值引入流动求解器解决方案。

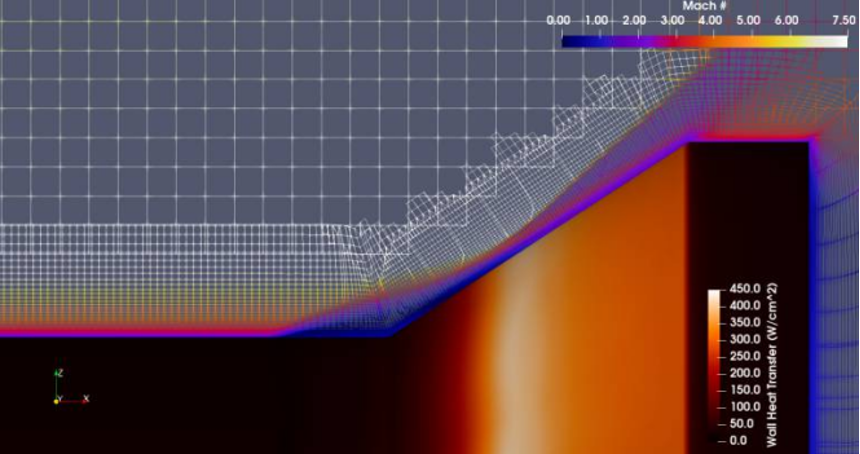
图 3.RavenCFD 模拟结果显示了 HIFiRE-1 耀斑区域的表面热通量和整体流动中的马赫数。

B. NASA 通用研究导弹 (CRM)

对于 CRM 几何形状，进行了三个模拟：

1. 具有插值函数裁剪的最小二乘供体加权
2. 无插值函数裁剪的双网格供体加权
3. 共形网格

同样在这种情况下，重叠网格边界被迫非常靠近 CRM，因此在这项工作中，重叠插值发生在高梯度区域。图 4 显示 CRM 网格（黑色）在越来越粗糙的笛卡尔背景网格的多个级别上靠近主体切割，随着与导弹主体的距离增加。

正如预期的那样，双网格的内存使用量更大，供体搜索时间也是如此。与 HIFiRE-1 案例相比，最小二乘法和双网格供体搜索算法之间的供体搜索时间差异增加可归因于 CRM 案例的组件网格数量增加。多级背景笛卡尔细化要求 Suggar++ 搜索多个重叠网格以寻找合适的供体。

图 4. CRM 模拟中的组件网格。

然而，再次使用双网格供体搜索算法有效地将插值函数限制在 0 和 1 之间，因此允许使用双网格进行 CRM 模拟，而无需剪裁插值函数。每个 CFD 模拟的结果都非常相似，重叠模拟表现出与保形模拟几乎相同的行为，尽管有一些轻微的振荡，很可能是由于高梯度区域的插值。总的来说，这项工作中显示的 RavenCFD 模拟表明，使用双网格方法时插值函数的边界可以消除引入流求解器的虚假极值，这会导致数值困难。

结论

将其因变量存储在单元格中心的流动求解器使用的重叠网格系统通常会使用插值供体。二阶插值要求可以使用最小二乘法来找到插值权重。这些插值权重通常不受 [0−1] 之间的限制，并且可以通过插值将新的极值引入到解中。去除极值的一种简单方法是将内插值裁剪为任何施主成员的最小值/最大值，这会将内插值降低到一阶。

使用 RavenCFD 代码针对高超音速条件下的锥体/圆柱体/耀斑和低超音速条件下的复杂导弹配置，研究了使用非结构化双网格插值的可压缩流 CFD 解决方案的有效性。这项工作比较了使用标准最小二乘供体和权重的结果，有和没有插值函数裁剪和全局双网格插值。对于这些可压缩的 CFD 解决方案，带裁剪的最小二乘插值是解决移动体问题的一种更具成本效益的方法，尽管在使用双网格方法时插值函数可以消除引入流动求解器的虚假极值。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删