布朗力分析新视角：CFD工具在粒子扩散中的应用

关键要点

流体中悬浮颗粒的随机运动会产生布朗力。
布朗运动的扩散性质可以用低雷诺数流体的 Stokes-Einstein 方程来解释。
通过在微观层面模拟粒子行为，可以预测复杂现实世界系统中的流体行为。

布朗力：使用 CFD 工具分析粒子扩散的图1

许多流体流动问题涉及对流动表现出的随机性和与之相关的力的研究。在更大范围内，这种随机性会影响接触物体的行为；例如，机翼穿过风或水流过转子叶片。从更微观的层面看，流体粒子可能由于粒子悬浮和分子碰撞而表现出随机性。这就是布朗力原理。

在计算流体动力学中，该原理可用于模拟颗粒悬浮及其随机性如何影响系统内的流动；例如，烟雾颗粒如何扩散到大气中或悬浮颗粒如何影响水的流动动力学。

让我们更深入地了解布朗力并了解其对流动模拟的重要性。

了解布朗力的本质

布朗力是流体由于分子碰撞而施加在悬浮粒子上的力。这种力是悬浮颗粒随机运动的结果，也称为布朗运动。布朗力在本质上是随机的，即粒子的随机运动导致力的方向和大小不断变化。一个热激发的分子足以启动这种随机运动，并且不需要主动力。

在许多情况下，这种力本质上是扩散的。扩散理论可以借助与流体接触的球形粒子的 Stokes-Einstein 方程来解释。在数值上，这表示为：

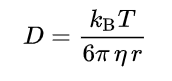
布朗力：使用 CFD 工具分析粒子扩散的图2

注意：

D是扩散系数

KB 是玻尔兹曼常数

T 是绝对温度

η 是动力粘度

r 是粒子的半径

重要的是要注意，该方程是针对低雷诺数流体假设的，即该方程对于速度较低的较小颗粒更为有效。该方程表明扩散系数对流体颗粒的温度和粘度以及悬浮颗粒的大小的依赖性。这种理解对于微流体系统设计或扩散分析领域中布朗力的模拟至关重要。

粒子布朗扩散的数值模拟

在流体系统设计中，布朗扩散分析对于理解混合等过程和相关扩散原理至关重要。该分析还允许在处理悬浮颗粒和相应的力时优化系统。使用 CFD 工具进行扩散分析有助于模拟布朗力引起的随机性，并对粒子行为进行数值分析。这可以通过多种方式完成。

直接数值模拟 (DNS) 技术是评估粒子布朗力的一种方法。DNS 方法使用Navier-Stokes 方程来计算流体和悬浮粒子的运动。使用高分辨率网格，可以在较小的尺度上模拟这种运动、粒子行为、边界层条件及其对流体系统的影响。虽然大涡模拟 (LES)可能会为此分析提供更准确的结果，但该方法最适合大规模模拟。结合了 DNS 和 LES 方法的混合方法更适合模拟布朗扩散，因为它提供了一种平衡的方法来确保大型或小型模拟的计算精度。