伯努利能量定理再认识：CFD学习中的能量守恒

关键要点

• 伯努利能量定理指出，与流体相关的总能量在流线的任何一点都保持不变。
• 在管道流中，可以应用伯努利能量定理来计算能量损失以及最小化这些损失以提高效率的方法。
• CFD模拟有助于验证伯努利能量定理在管流分析中的准确性。

流体流动分析在许多工程应用中至关重要，尤其是在管道系统的设计中。管道流动行为对管道系统的安全性和运行效率具有重大影响。此类系统的高效设计和优化需要深入了解复杂的流动模式、流体特性、边界条件和管道几何形状的作用——这些因素是管道流分析的重大挑战。

伯努利能量定理提供了一个理论框架来理解流动过程中不同点的能量平衡。了解不同参考点的速度、压力和流速，使流体系统工程师能够预测流经管道时的流动行为，并设计出符合安全和性能标准的系统。在本文中，我们将探讨伯努利能量定理的关键概念及其在管道流分析中的应用。

解释伯努利能量定理

在流体动力学中，伯努利能量定理或伯努利原理处理与流体流动相关的能量守恒概念。它指出，对于稳定的、流线型的、不可压缩的流体，流体的能量总和（势能 + 动能 + 压力）在流线的任何一点都保持不变。在数学上，这个定理可以表示为：

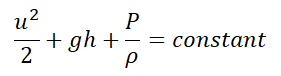
伯努利能量定理

u 是流体的速度

g 是重力加速度

h 是参考点上方的流体高度

P 是给定点的流体压力

ρ 是流体密度

为使定理成立，应满足以下条件：

1. 没有热传递
2. 不施加外力
3. 流动过程中无摩擦损失

在管道流分析中，可以应用伯努利能量定理来找出压力和速度变化的区域。该计算可用作概述速度分布和预测管道中 流动行为的基础。

伯努利能量定理简化管道流量分析

伯努利能量定理以能量守恒的概念为参考，详细说明了沿管道长度发生的能量损失。在现实世界中，湍流或摩擦等因素很难实现完美的能量平衡。使用伯努利能量定理，工程师可以在管道流分析中分析以下内容。

可以使用CFD模拟工具对影响管道流动参数的这些因素进行分析。

使用 CFD 仿真验证伯努利能量定理

CFD 模拟工具使用数值方法来求解与流体流动相关的控制方程。通过分析流动行为并计算管道系统中不同点的能量和流量，工程师可以验证伯努利能量定理的准确性。

CFD 仿真提供了速度分布和压力等值线的详细可视化，这解释了管道系统中的能量损失。将 CFD 模拟与伯努利能量定理的理论框架进行比较，可以深入了解为实现所需效率而需要平衡的能量损失的大小。工程师和设计师可以利用 Cadence 的 Fidelity 和 Fidelity Pointwise 等工具进行完整的仿真和数值分析，以支持高度可靠的管道系统设计。  

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删