ANSYS知识普及：粘弹性人工边界的实现方法

本人准备出一个ANSYS知识普及系列，将有用的网上资料归拢，由于知识水平有限，不对之处请谅解。也欢迎各位网友提供好的资料分享，让我们共同完成这个ANSYS知识普及系列。

业务咨询网址：http://www.jishulink.com/content/other/402981

从半空间无限域取一4X2的矩形平面结构，顶部中间一定范围内受随时间变化的均布荷载，荷载如下

p(t)=t        当0< DIV>

p(t)=2-t        当1<=t<=2时

p(t)=0        当t>2时

材料弹性模量E=2.5，泊松比0.25，密度1

网格尺寸0.1X0.1，在网格边界上所有结点加法向和切向combin14号单元用以模拟粘弹性人工边界（有关理论可参考刘晶波老师的相关文章）。combine14单元的两个结点，其中一个与实体单元相连，另一个结点固定。网格图如图1所示

时程分析的时间步长为0.02秒，共计算16秒。计算得到四个控制点位移时程图如图2所示，控制点坐标A(0,2)、B(0,1)、C(0,0)、D(2,2).

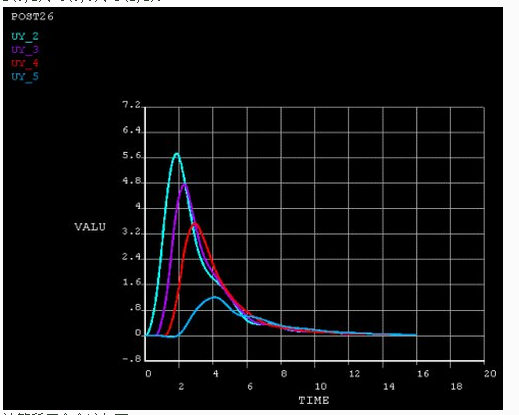
计算所用命令流如下：

/PREP7 L=4      !水平长度 H=2          !竖起深度 E=2.5     !弹性模量 density=1   !密度 nu=0.25    !泊松比 dxyz=0.1   !网格尺寸

G    = E/(2.*(1.+nu))    !剪切模量 alfa = E*(1-nu)/((1.+nu)*(1.-2.*nu))  !若计算平面应力，此式需要修改 Cp=sqrt(alfa/density)    !压缩波速 Cs=sqrt(g/density)     !剪切波速 R=sqrt(L*L/4.+H*H/4.)    !波源到边界点等效长度

KbT=0.5*G/R*dxyz KbN=1.0*G/R*dxyz CbT=density*Cs*dxyz CbN=density*Cp*dxyz

ET, 1, plane42,,,2   !按平面应变计算 et, 2, combin14, ,, 2    !切向 et, 3, combin14, ,, 2    !法向 r, 2, KbT, CbT r, 3, KbN, CbN

  MP, EX, 1, E MP, PRXY, 1, nu MP, DENS, 1, density

rectng,-L/2.,L/2,0.,H

asel, all aesize, all, dxyz mshape,0,2D mshkey,1 amesh, all

!以下建立底边界法向和切向弹簧阻尼单元 nsel,s,loc,y,0. *get,np,node,,count      !得到选中的结点数，存入np *get,npmax,node,,num,maxd    !得到已经定义的最大结点数，存入npmax *do,ip,1,np  npnum=node((ip-1)*dxyz-L/2.,0.,0.)  x=nx(npnum)  y=ny(npnum)  z=nz(npnum)  npmax=npmax+1  n,npmax,x.,y-dxyz/2,z    !定义底边界法向结点以便与边界点形成法向单元  type,3  real,3  e,npnum,npmax  d,npmax,all,0.       !约束新生成的点  npmax=npmax+1  n,npmax,x-dxyz/2.,y,z    !定义底边界切向结点以便与边界点形成切向单元  type,2  real,2  e,npnum,npmax  d,npmax,all,0.       !约束新生成的点 *enddo

!以下建立左边界法向和切向弹簧阻尼单元 nsel,s,loc,x,-L/2 *get,np,node,,count      !得到选中的结点数，存入np *get,npmax,node,,num,maxd    !得到已经定义的最大结点数，存入npmax *do,ip,2,np       !侧边界最下面一个点按底边界上处理  npnum=node(-L/2,(ip-1)*dxyz,0.)  x=nx(npnum)  y=ny(npnum)  z=nz(npnum)  npmax=npmax+1  n,npmax,x-dxyz/2.,y,z    !定义左边界法向结点以便与边界点形成法向单元  type,3  real,3  e,npnum,npmax  d,npmax,all,0.       !约束新生成的点  npmax=npmax+1  n,npmax,x,y-dxyz/2.,z    !定义左边界切向结点以便与边界点形成切向单元  type,2  real,2  e,npnum,npmax  d,npmax,all,0.       !约束新生成的点 *enddo

!以下建立右边界法向和切向弹簧阻尼单元 nsel,s,loc,x,L/2 *get,np,node,,count      !得到选中的结点数，存入np *get,npmax,node,,num,maxd    !得到已经定义的最大结点数，存入npmax *do,ip,2,np       !侧边界最下面一个点按底边界上处理  npnum=node(L/2,(ip-1)*dxyz,0.)  x=nx(npnum)  y=ny(npnum)  z=nz(npnum)  npmax=npmax+1  n,npmax,x+dxyz/2.,y,z    !定义右边界法向结点以便与边界点形成法向单元  type,3  real,3  e,npnum,npmax  d,npmax,all,0.       !约束新生成的点  npmax=npmax+1  n,npmax,x,y-dxyz/2.,z    !定义右边界切向结点以便与边界点形成切向单元  type,2  real,2  e,npnum,npmax  d,npmax,all,0.       !约束新生成的点 *enddo

allsel,all /pnum,type,1 /number,1 eplot finish

/solu

ANTYPE,trans !*  TRNOPT,FULL LUMPM,0

btime=0.02 etime=16.00 dtime=0.02 *DO,itime,btime,etime,dtime  TIME,itime  nsel,s,loc,y,H      !选中需要加荷载的点  nsel,r,loc,x,-L/4,L/4  *if,itime,lt,1.,then   f,all,fy,1*itime  *elseif,itime,ge,1.0,and,itime,le,2.0   f,all,fy,1*(2-itime)  *else   f,all,fy,0.0  *endif  allsel,all  SOLVE *ENDDO

另外，还用自己编写的有限元程序计算了一下这个例子，并与ANSYS得到的结果进行了比较，结果非常吻合，这里给出A点的比较结果。

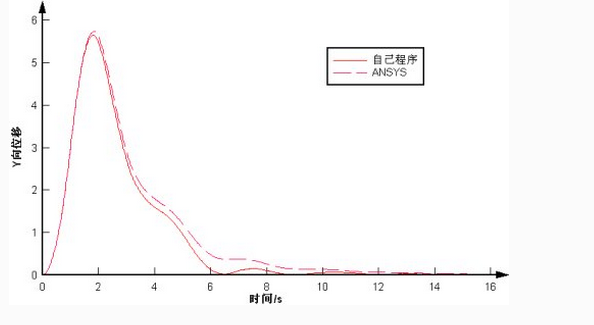
免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删