ANSYS Workbench橡胶超弹分析实战

典型橡胶材料超弹性本构模型及其适用性
   

橡胶又称为弹性体，包括天然橡胶及合成橡胶，是无定形的高聚物。橡胶是一种超弹性材料，具有良好的伸缩性和复原性，被广泛用作密封、减振部件。相对于金属材料的性能表征只需要较少的参数，橡胶的特性就显得很错综复杂，其物理化学性能与金属材料有很大差别。

橡胶材料的主要特点：

1) 不可压缩性：橡胶材料的泊松比μ一般在0.45～0.4999范围内变化，接近于液体的泊松比0.5，因此橡胶可以看作是一种体积近似不可压缩的材料。

2) 大变形特性：橡胶高分子材料变形很大，而其弹性模量与金属材料相比却小很多。橡胶材料的变形范围一般在200%～500%，甚至能够达到1000%，很多金属材料的变形则不足0.5%

3) 非线性：橡胶材料具有三重非线性，即几何非线性、材料非线性和边界非线性。橡胶材料的应力-应变关系具有明显的非线性，其力学性能与环境条件、应变历程、加载速率等因素有很大关联，且随时间延长而不断变化。

橡胶材料本构模型及其适用性

从20世纪40年代至今，国内外许多学者提出了许多橡胶材料的本构模型，大致可分为两大类：基于应变能函数的唯象模型和基于分子链网络的统计模型。

基于应变能函数的唯象模型又可分为两类。一类是以应变不变量表示的应变能密度函数模型，这类模型在处理橡胶弹性时，可以把橡胶材料的变形看成是各向同性的均匀变形，从而将应变能密度函数表示成变形张量不变量的函数，比如：Mooney-Rivlin模型、Yeoh模型等。另一类是以主伸长表示的应变能函数模型，比如：Valanis-Landel模型、Ogden模型等。

基于分子链网络的统计模型按照分子链的统计特性可分为两类：高斯链网络模型和非高斯链网络模型。其中最具代表性的分子统计学模型包括Treloar模型以及Arruda-Boyce模型。

下面对几种常见的本构模型进行简要介绍。

Mooney-Rivlin模型

Mooney-Rivlin模型是一个比较常用的模型，几乎可以模拟所有橡胶材料的力学行为。其应变能密度函数模型为：

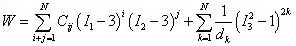
对于不可压缩材料，典型的二项三阶展开式为：

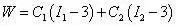
式中：N、Cij和dk为材料常数，由实验确定。

Mooney-Rivlin模型适合于中小变形，一般适用于应变约为100%(拉伸)和30%(压缩)的情况。但该模型不能模拟多轴受力数据，由某种试验得到的数据不能用来预测其它的变形行为。对于没有加碳黑的橡胶来说，该模型能得到比较准确的结果，但不能精确模拟加了碳黑的橡胶。

Yeoh模型
 

Yeoh模型比较适合模拟炭黑填充NR的大变形行为，并具有用简单的单轴拉伸试验数据描述其他变形的力学行为的能力。其应变能密度函数模型为：

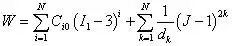
J是变形后与变形前的体积比，对不可压缩材料，J=1，典型的二项参数形式为：

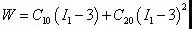
式中：N、Ci0和dk为材料常数，由材料试验所确定，初始剪切模量μ=2C10。

Yeoh模型能描述随变形而变化的剪切模型的填料橡胶，如加碳黑后的橡胶。而且，该模型可通过某种简单变形实验数据拟合的参数来预测其他变形的力学行为，描述的变形范围也较宽。但Yeoh模型对等双轴拉伸实验的结果不能很好的解释，不能准确描述小变形时的情况。

Ogden模型
 

Ogden R W不作应变能函数是主伸长偶函数的假设，提出以主伸长来表征应变能函数，如下式所示：

式中：μi和αi为材料常数，αi可取任何实数值。

Ogden模型与Mooney-Rivlin模型并没有本质上的区别，仅在有限元分析中根据系数拟合的难易程度选择合适的模型。

2ANSYS Workbench超弹性分析
   
ANSYS超弹性材料模型

ANSYS超弹性材料模型有很多种类，如图1，主要包括Polynomid Form模型、Mooney-Rivlin模型、Neo-Hookean模型、Yeoh模型、Arruda-Boyce模型、Gent模型、Ogden模型、Blatz-Ko模型。在不同情况下模型的选取材料数据的获得参数拟合及不同橡胶材料选用不同模型的应用实例用户应根据实际材料的实验特性等来选择合适的模型。对于超弹应用而言，ANSYS程序本身从求解器、单元技术以及解算策略等方面都进行了完善的设计，具有很好的效率和效果。

图1 ANSYS超弹性材料

双参数Mooney-Rivlin模型与拉伸实验数据在100%应变范围内的相关性都很好，但描述压缩变形时却很不够，它也无法解释大的形变时材料的硬化行为。3项或多项Mooney-Rivlin模型可描述非常数剪切模量。然而，引入高次项后需小心计算。因其可能会导致不稳定能函数的产生，得到超出试验范围的非物理结果。

Gent和Yeoh均指出，高次应变能函数的应用价值很小，因为类橡胶材料的重现性是不足够的，不允许对大量的参数进行精确的估计。因此，附加项只是用来修正实验误差。由于简单和实用，在FEA中应用最广泛的应变能函数应该首选Mooney-Rivlin模型，尽管众所周知它并不精确。

Polynomial Form模型适用的应变范围与多项式阶次N相关，可达300%。

Neo-Hookean模型，其第1个参数等于剪切模量的1/2，而第2个参数为0。这种材料模型又有通常的剪切模量，在单相拉伸中应变直到40%，在简单剪切中应变直到90% 时，都有很好的相关性。

Yeoh模型与其他高次模型的区别在于，它只依赖于第1个应变常数，经论证当只用来自单轴拉伸试验的数据时，此模型适合各种不同的变形方式。这就减少了材料试验的需求条件。低应变下应用此模型时需特别细心。

在简单拉伸中，Ogden模型可在应变直到700%时还与试验数据很相符。它还适应非常数剪切模量和轻微压缩的材料行为。它已经被成功地应用于O 形圈、密封圈和其他工业产品的分析。

ANSYS Workbench参数拟合功能

利用ANSYS提供的线性和非线性回归算法，用户可直接输入超弹材料的试验数据以获得其材料参数值，且该功能适用于所有超弹模型。用户将试验数据存放在一个文本文件中，可以针对多种超弹模型作曲线拟合，程序同时提供拟合的误差范数并以图形的方式显示试验数据与所计算的系数之间的关系，以便选取合适的超弹性模型。

3ANSYS Workbench橡胶超弹性分析实例
   

问题描述

使用ANSYS Workbench模拟橡胶材料试件的拉伸试验，取四分之一模型进行建模，如下图所示，在右侧位置施加一定位移，计算得到产生位移后的状态。

图2 几何模型

分析步骤
   

1）创建静力学分析流程。

2）设置材料属性：根据实验得到的数据，分别输入单轴、双轴、剪切的实验数据，得到各个实验数据曲线，然后应用曲线拟合功能，得到计算用的材料曲线，以及相关参数。

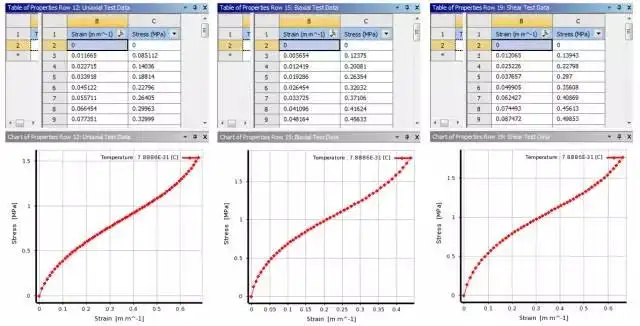
图3 输入材料实验数据

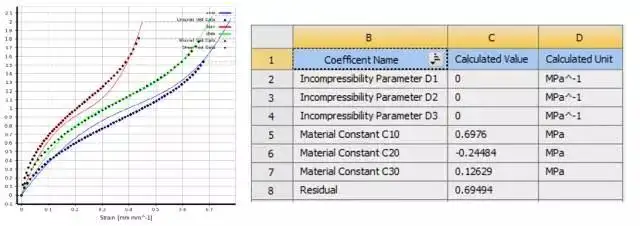
图4 曲线拟合

3）划分网格：采用扫掠方式，取合适的网格密度，得到全六面体单元网格。

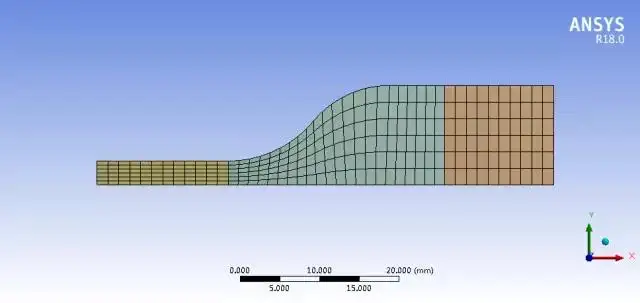
图5 划分网格

4）施加约束及载荷：在对称面上施加无摩擦约束，在右侧施加位移约束。

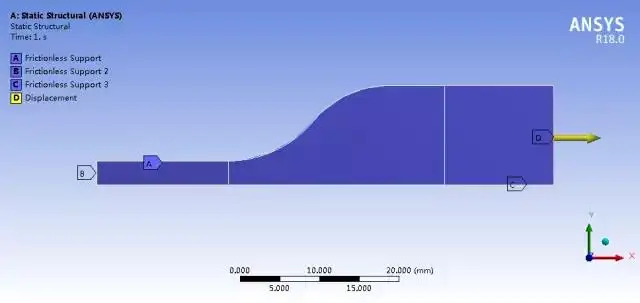
图6 边界条件

5）计算求解：打开大变形开个，打开自动时间步，调整最小子步数等。

6）结果后处理：查看等效应力及等效应变。

图7 变形云图

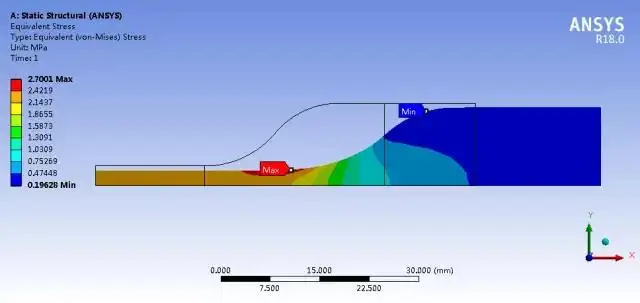
图8 等效应力云图

4结论
   

ANSYS提供了丰富的超弹性材料，强大的曲线拟合功能，以及各种非线性分析设置，利用Workbench平台操作的便利性，可以方便的进行各种橡胶材料或超弹性模型的分析。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删