产品
ADAMS的函数种类比较多：
1、Displacement Functions
2、Velocity Functions
3、 Acceleration Functions
4、 Contact Functions
5、 Spline Functions
6、 Force in Object Functions
7、Resultant Force Functions
8、 Math Functions
9、 Data Element Access
10、User-Written Subroutine Invocation
11、Constants & Variables
一、 几个常用函数的说明
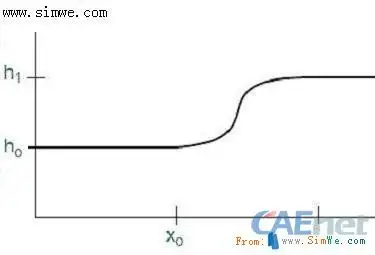
1、 STEP函数
格式：STEP (x, x0, h0, x1, h1)
参数说明：
x ―自变量，可以是时间或时间的任一函数
x0 ―自变量的STEP函数开始值，可以是常数或函数表达式或设计变量；
x1 ―自变量的STEP函数结束值，可以是常数、函数表达式或设计变量
h0 ― STEP函数的初始值，可以是常数、设计变量或其它函数表达式
h1 ― STEP函数的最终值，可以是常数、设计变量或其它函数表达式
2、 IF函数
格式：IF(表达式1: 表达式2, 表达式3, 表达式4)
参数说明：
表达式1－ADAMS的评估表达式；
表达式2－如果的Expression1值小于0，IF函数返回的Expression2值；
表达式3－如果表达式1的值等于0，IF函数返回表达式3的值；
表达式4－如果表达式1的值大于0，IF函数返回表达式4的值；
例如：函数 IF(time-2.5:0,0.5,1)
结果： 0.0 if time < 2.5
0.5 if time = 2.5
1.0 if time > 2.5
3、AKISPL函数
格式：AKISPL (First Independent Variable, Second Independent Variable，Spline Name, Derivative Order)
参数说明：
First Independent Variable —— spline中的第一个自变量
Second Independent Variable (可选) —— spline中的第二自变量
Spline Name —— 数据单元spline的名称
Derivative Order (可选) —— 插值点的微分阶数，一般用0就可以了
例如：
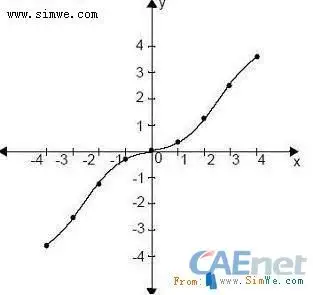
function = AKISPL(DX(marker_1, marker_2, marker_2), 0, spline_1)
spline_1用下表中的离散数据定义
自变量(x): 函数值 (y):
-4.0 -3.6
-3.0 -2.5
-2.0 -1.2
-1.0 -0.4
0.0 0.0
1 0.4
2 1.2
3 2.5
4 3.6
二、实例说明
1、分段函数的表示
在ADMA中如何输入力或位移、速度、加速度等的分段曲线，这一直是一个值得注意的问题。
下面用一个小例子进行简单说明：（这个例子实际上就是常见的加速－匀速－减速问题）
1) 要输入的速度函数为：
10＊t (0<t<0.1)
V= 1 (0.1<t<0.4)
-10＊t+5 (0.4<t<0.5)
2) 在ADMAS中的表示：
velo(time)=if(time-0.1:step(time,0,0,0.1,1),1,step(time,0.4,1,0.5,0))
3) 得到的速度曲线如下图：
step_if_use.rar
2、方形波函数的输入
1) 有时需要输入下方波形式的力或力矩，如果单纯地采用STEP函数迭加是不能实现的
2) 在ADAMS中输入的函数形式为：
step(sin(2*pi*time),-0.01,-1,0.01,1)
注意点：
⑴当方波的频率改变时，可以通过改变下式中的FREQ得以实现
sin(2*pi*FREQ*time)
⑵改变方波的上下限的方法：
step(sin(2*pi*time),-0.01,LOWER,0.01,UPPER)
⑶例如：
step(sin(2*pi*3.0*time),-0.01,0,0.01,7) 中的频率为3HZ，上下限分别为0,7
3) 在ADAMS中所得到的方波曲线如下：
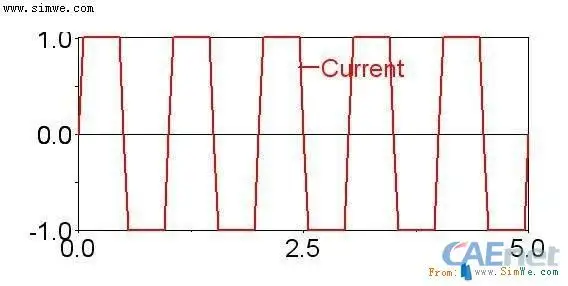
3、 AKISPL函数的应用
有时做路径规划或输入力或力矩时，需要用到AKISPL函数，数据单元SPLINE实际上可根据多种渠道创建，如经验数据、实验数据等都可以。
CMD文件见lujing_1.cmd:
建立SPLINE时所用的数据：
Time Dis_X
0 0
0.263157895 264.6382854
0.526315789 529.0483902
0.789473684 751.4278083
1.052631579 781.2404309
1.315789474 619.0122219
1.578947368 552.1253792
1.842105263 718.4079735
2.105263158 983.8161748
2.368421053 1248.462634
2.631578947 1513.142799
2.894736842 1777.653155
3.157894737 2034.291889
3.421052632 2156.967539
3.684210526 2085.106599
3.947368421 2025.181599
4.210526316 2146.663913
4.473684211 2375.226147
4.736842105 2634.081904
5 2900
Time Dis_Z
0 0
0.263157895 -7.67E-04
0.526315789 0.613674188
0.789473684 102.2423923
1.052631579 352.6958661
1.315789474 558.5047146
1.578947368 807.3775974
1.842105263 1002.119048
2.105263158 1000.01823
2.368421053 1000.009096
2.631578947 1000.267792
2.894736842 999.4879245
3.157894737 962.0426698
3.421052632 736.5248822
3.684210526 484.6759224
3.947368421 264.2985997
4.210526316 38.2516224
4.473684211 4.175972774
4.736842105 -1.187352978
5 0
动画演示：
免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删
155-2731-8020
