引言:
我们知道从1914年Ingless和1921年Griffith提出断裂力学开始,一直到60年代都停留在线弹性断裂力学(LEFM)的层次。后来由於发现在裂纹尖端进入塑性区后用LEF仍然无法解决stress singularity的问题。1960年由Barenblatt 和Dugdale率先提出了nonlinear/plastic fracture mechnics的概念,在裂纹前端引入了plastic zone,这也就是我们现在用的 cohesive fracture mechnics的前身。当时这个概念还没引起学术界的轰动。直到1966年Rice发现J-integral及随后发现在LEFM中J-integral是等于energy release rate的关系。随后在工程中发现了越来越多的LEFM无法解释的问题。 cohesive fracture mechnics开始引起更多的关注。在研究以混凝土为代表的quassi-brittle material时,cohesive fracture mechnics提供了非常好的结果,所以在70年代到90年代,cohesive fracture mechnics被大量应用于混凝土研究中。目前比较常用的方法主要是fictitious crack approach和effective-elastic crack approach或是称为equivalent-elastic crack approach. 其中fictitious crack approach只考虑了Dugdale-Barenblatt energy mechanism而effective-elastic crack approach只考虑了基於LEFM的Griffith-Irwin energy dissipation mechanism,但作了一些修正。
做裂纹ABAQUS有几种常见方法。最简单的是用debond命令, 定义
*FRACTURE CRITERION, TYPE=XXX,
参数。。。
**
*DEBOND, SLAVE=XXX, MASTER=XXX, time increment=XX
0,1,
……
......
time,0
要想看到开裂特别注意需要在指定的开裂路径上定义一个*Nset, 然后在
*INITIAL CONDITIONS, TYPE=CONTACT中定义
master, slave, 及指定的Nset
这种方法用途其实较为有限。
例子如图

另一种方法,在interaction模块,special, 定义crack seam, 网格最好细化,用collapse element模拟singularity. 这种方法可以计算J积分,应力强度因子等常用的断裂力学参数.
裂尖及奇异性定义:
在interaction-special,先定义crack, 定义好裂尖及方向, 然后在singularity选择:
midside node parameter: 输入0.25, 然后选Collapsed element side, duplicate nodes,8节点单元对应(1/r)+(1/r^1/2)奇异性。
这里midside node parameter选0.25对应裂尖collapse成1/4节点单元。如果midside nodes不移动到1/4处, 则对应(1/r)奇异性, 适合perfect plasticity的情况.
网格划分:
裂尖网格划分有一些技巧需要注意,partition后先处理最外面的正方形,先在对角线和边上布点,记住要点constraint, 然后选第三个选项do not allow the number of elements to change不准seed变化,密度可以自己调整. 最里面靠近圆的正方形可以只在对角线上布点. 也可以进一步分割内圆及在圆周上布点. 里面裂尖周围的内圆选free mesh, element type选cps6或者cpe6,外面四边形选sweep mesh, element type选cps8或者cpe8, 记住把quad下那个缩减积分的勾去掉。例子如图

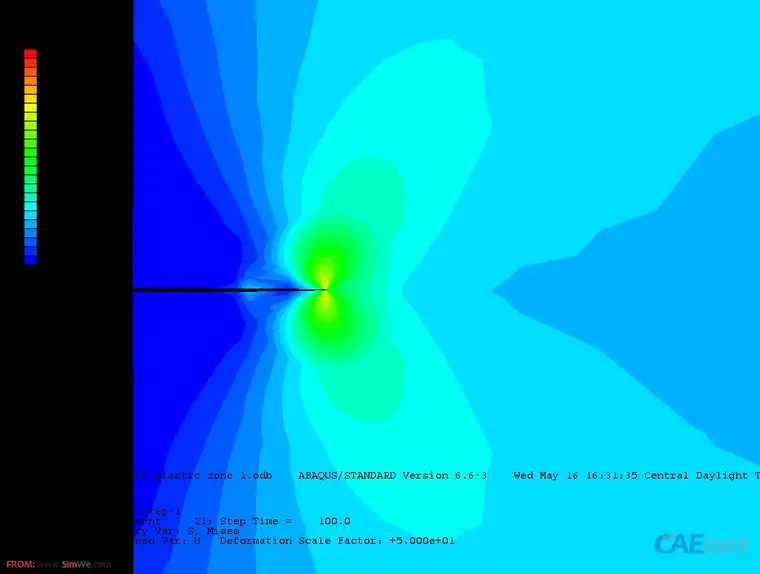


这种方法的几个值得注意的问题,见不少朋友问过。主要是对断裂力学的理解问题。
1.为什么设置理想弹塑性(epp)分析的时候得到的xx,yy方向或者最大应力值Sxx, Syy会超过材料的屈服强度Sy呢, 这分析结果可能吗?
这是因为在ABAQUS中对应等于材料的屈服强度的是von Mises等效应力Se=Sy,因此在 平面应变的条件下,xx方向的应力Sxx=Sy*pi/SRQT(3)>Sy, 而Syy=Sy*(2+pi)/SRQT(3), 大概是3倍的屈服应力。所以得到大于材料的屈服强度的xx及yy方向应力是正常的。
2.为什么设置collapse element的时候对弹性分析在中间就一个点而要把单元边上的中点移到1/4处,但弹塑性分析却要在中间设置一圈点并且保持单元边上的中点位置不变呢?
这个其实不是随便定的,在有限元中分析裂纹时,对弹性分析需要模拟裂尖1/SQRT(r)的奇异性,这样在把单元边上的中点移到1/4处后计算出来的等参单元拉格郎日型函数对应的u field正好包含1/ SQRT(r)项,事实上这一方法在断裂力学的数值模拟发展史上是很巧妙的一个发现,至今仍然被广泛采用。至于理想弹塑性分析需要模拟裂尖1/r的奇异性, 这样大家都知道在把单元边上的点放在到1/2处后计算出来的正常的等参单元拉格郎日型函数对应的u field包含1/ r项, 可以模拟弹塑性分析需要的裂尖1/r的奇异性。所以在看似动手点几下就能实现的分析模式后面有很清楚漂亮的理论作支持。
也可以使用python控制seam尺寸,然后移动partition和网格,我也没尝试过。但有一些学者有类似的结果:FRANC/FAM - A software system for the prediction of crack propagation.
In: Journal of Structural Engineering 26, No. 1, 1999, pp. 39-48.
再不就是用一些专业的断裂力学软件如zencrack,感兴趣的可以自己找相关资料
还有就是比较新的cohesive element单元。我仔细读了 ABAQUS cohesive element的理论帮助,个人意见ABAQUS的cohesive element采用的是广泛应用于混凝土的类似fictitious crack的方法。只考虑了Dugdale-Barenblatt energy mechanism。 这其中softening law 的影响是非常重要的。
但ABAUQS似乎只提供了linear 或者exponential 的softening law,复杂的本构关系还需要另想办法。至於基于Griffith-Irwin energy dissipation mechanism的J-integral值可以在LEFM分 析中单独算。
(ABAQUS用的是Suo Zhigang 和Hutchinson在1990一篇论文中提出的方 法) 目前cohesive fracture mechnics已经被应用于各种材料。不过在使用到纳米 或者更小数量级的研究中碰到了不少问题,可能需要结合位错和分子动力学的一些 理论。
现有的cohesive element单元需要定义damage initiation和evolution的准则, softening准则目前好像只有linear和exponential,但对一般材料也够用了。然后通过设置后处理display group可以看到裂纹扩展情况。
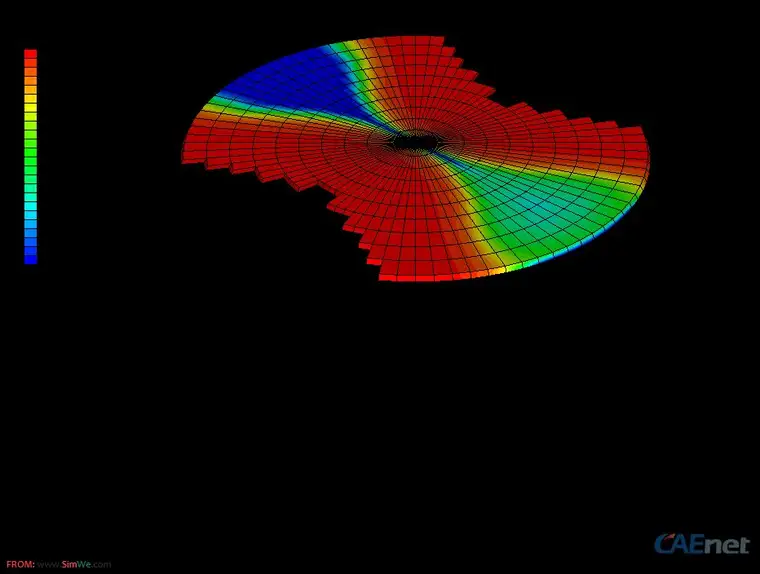
裂纹扩展不是ABAQUS的强项,目前比较方便的只能用cohesive element,我做过几个模型效果还可以,但对应的参数需要一定的实验数据支持,否则做出来了也不知道对不对。要注意geometric thickness和constitutive thickness; material stiffness和interfacial stiffness的区别 以及厚度与精度的影响。Cohesive element的核心主要是TS-Law,无论里面的数据如何选取,厚度如何变化,cohesive element的表现取决于TS-Law的定义。具体dava的popo10已经给过详细的解释的讨论,可以搜索他们的帖子。如图是我做的3d cohesive element interfacial crack 的例子。

免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删