摘 要:高压制冷装置通过管路给红外探测器供气制冷,将探测器元件冷却至低温或深低温,使热成像系统正常工作。高压气瓶为高压制冷装置储存和提供高压气体,是高压制冷装置的主要组件。详细阐述了高压气瓶的结构设计方法并进行不同载荷的仿真试验,同时根据拉梅公式对气瓶的爆破形态进行理论分析,最后通过瓶体爆破试验加以验证。
关键词:红外探测技术;制冷气瓶;拉梅公式;爆破形态;仿真验证;
0 引言
红外热成像制冷技术是指通过物理或化学的手段将探测器元件冷却至低温或深低温的技术[1],其目的一方面能够保证电子器件与系统功能的正常,提高元器件的灵敏度,另一方面可以屏蔽或减少来自热成像系统的滤光片、挡板及光学系统本身带来的热噪声[2]。
高压制冷装置是红外热成像制冷技术的一种常用的物理制冷方法,能够给红外探测器制冷,低温环境可降低红外探测器的噪声,提高探测器的灵敏度和分辨率[3]。高压制冷装置的主要结构为高压制冷气瓶,瓶体内部储存着高压气体。
1833年法国巴黎大学教授G.拉梅(Lame)和克拉伯龙(Clapeyron)根据弹性理论,推导出了厚壁圆筒在受到内外压强作用时任意半径处的三向应力计算公式,即拉梅公式(Lame formula),为压力容器的结构设计提供了理论基础,促进了压力容器的发展,使得压力容器广泛应用于各个行业[4]。
高压容器的可靠性设计越来越受到人们的重视[5,6,7],在设计过程中应保证结构强度的可靠性与安全性、高压气体流通部位的密封性以及气瓶材料的综合力学性能等。为了保证和满足高压容器设计、生产和检验等方面的一致性和基本要求,国内现行的国家标准有GB150—1998《钢制压力容器》以及JB4732—1995《钢制压力容器分析设计标准》,其中GB150—1998要求设计压力小于35 MPa, 而JB4732—1995的设计压力要求小于100 MPa, 设计压力范围更加广泛[8,9,10]。在失效设计准则方面,GB150—1998采用弹性失效设计准则,而JB4732—1995采用塑性失效准则。弹性失效设计准则要求压力容器任一位置的材料不允许达到屈服极限,而塑性失效设计准则是以内外壁的整体屈服作为容器达到极限承载能力的一种强度设计准则,该设计准则认为容器的某一部分发生屈服而其他部分仍处于弹性状态时,依然可以继续提高承载能力。因此在相同条件下,依据JB4732—1995设计的压力容器瓶体结构较薄,质量较轻。
由于高压气瓶内部储存着高压气体,具有一定的危险性,因此在设计瓶体结构时不仅需要保证瓶体在工作压力作用下的强度,还需考虑瓶体在发生爆破时的爆破形态。通常要求高压气瓶在发生爆破时无碎片产生,爆破位置处成撕裂状,以有效降低安全事故发生的概率。
本文参照压力容器设计标准对高压制冷装置的气瓶结构展开设计,并进行瓶体仿真试验以保证瓶体在工作压力作用下结构强度的可靠性与安全性,同时针对气瓶的爆破形态进行理论分析,并加以试验验证。
1 高压气瓶的结构设计
本文拟定气瓶在20 ℃温度下工作,工作压力为50 MPa, 容积为(200±5)mL,气瓶发生爆破时爆破口呈撕裂状且无碎片产生。瓶体材料选择0Cr17Ni4Cu4Nb, 该材料的屈服极限为1 000 MPa, 强度极限1 070 MPa。高压制冷装置的循环使用次数较少,忽略疲劳破坏对结构强度的影响,气瓶结构主要为前后两个半瓶体零件采用电子束焊接[11]成型,气瓶结构如图1所示。本文对气瓶的充气和放气等结构暂不作设计说明。
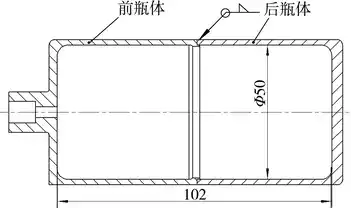
图1 气瓶结构简化示意图
1.1 高压气瓶瓶身厚度设计
气瓶瓶身厚度设计依据钢制气瓶设计标准JB4732—1995进行,即
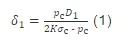
式中:δ1为气瓶瓶身厚度,mm;pc为计算压力,pc=50 MPa;D1为瓶体内径,D1=50 mm;K为载荷组合系数,取K=1; σc为设计应力强度,MPa。
根据气瓶设计标准JB4732—1995,设计应力强度为下列各值的最低值:
1)常温下抗拉强度最低值的1/2.6,MPa;
2)常温下屈服极限最低值的1/1.5,MPa;
3)设计温度下屈服极限的1/1.5,MPa。
因此可以得到设计应力强度的计算表达式为
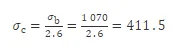
将以上数值带入式(1)中进行计算得到
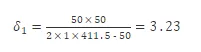
根据上述计算可以得到气瓶瓶身设计厚度为3.23 mm,由于气瓶内部充入高纯度氩气,因此可以忽略腐蚀裕量,故最终取瓶身厚度为3.5 mm。
1.2 高压气瓶端盖厚度设计
高压气瓶端盖厚度设计仍参照钢制气瓶标准JB4732—1995进行,气瓶端盖采用如图1所示结构,由设计公式:
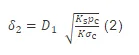
式中:δ2为气瓶端盖厚度,mm;Ks为结构特征系数,根据气瓶设计标准JB4732—1995取Ks=0.11。
将上述各相关数据带入式(2)中进行计算,可以得到:

经过上述计算得到气瓶端盖设计厚度为5.78 mm,与气瓶瓶身相同忽略腐蚀裕量,故最终取气瓶端盖厚度为6.0 mm。根据瓶身及端盖的设计尺寸,取内部圆角R=6.0 mm。
2 高压气瓶的仿真分析
对瓶体的三维设计图进行适当的简化,对充放气口结构进行了封堵。为了保证气瓶在充入高压气体时的安全性与可靠性,对瓶体分别进行1.5倍和2.5倍工作压力试验,要求瓶体在2.5倍工作压力作用下不允许发生破裂失效,因此仿真载荷工况包括:气瓶在50 MPa、75 MPa以及125 MPa内压作用下的使用极限静载条件。应用ABAQUS Static求解器,在高压气瓶内壁面施加均匀压强进行仿真分析。
2.1 瓶体50 MPa内压载荷工况分析
气瓶在50 MPa内压载荷作用下最大Mises应力出现在如图2所示的上端结构与瓶体主结构连接处,最大应力值为922 MPa,接近瓶体材料屈服极限1 000 MPa。主要原因是上端结构与瓶体端盖刚度不匹配,存在着较大的应力集中现象。根据图2可以得到上端结构与瓶体主结构连接处的高应力区域分布在倒角的表层局部,并未穿透整个瓶壁。高压气瓶在50 MPa内压作用下焊缝连接区域如图3所示, Mises应力最大值为370 MPa,未达到材料的屈服极限。因此可以保证瓶体在工作压力下的安全性与可靠性。

图2 连接倒角处剖面图(50 MPa)
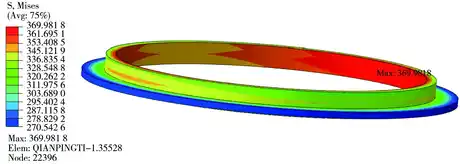
图3 焊接位置处剖面图(50 MPa)
2.2 瓶体75 MPa内压载荷工况分析
在75 MPa压力作用下的气瓶最大Mises应力出现在如图4所示的上端结构与瓶体主结构连接处,最大应力值为1 125 MPa,已达到材料的屈服极限。上端结构与瓶体主结构连接处的塑性区域分布在倒角的表层局部,并未穿透整个瓶壁。焊缝连接区域如图5所示,应力最大值为555 MPa,未达到材料的屈服极限,因此根据塑性失效设计准则,瓶体在75 MPa载荷作用下,具有一定的安全性与可靠性。

图4 连接倒角处剖面图(75 MPa)

图5 焊接位置处剖面图(75 MPa)
2.3 瓶体125 MPa内压载荷工况分析
瓶体在125 MPa内压载荷作用下如图6所示,上端结构与瓶体主结构连接处,最大应力值为1 170 MPa,超过材料屈服极限。如图7所示上端结构与瓶体主结构连接处的塑性区域分布未穿透整个瓶壁。焊缝连接区域如图7所示Mises应力最大值为925 MPa。

图6 连接倒角处剖面图(125 MPa)
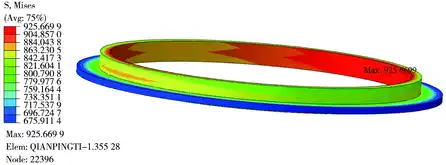
图7 焊接位置处剖面图(125 MPa)
经过以上仿真分析,可以得到瓶体在50 MPa工作压力作用下,瓶体结构最大应力未达到材料的屈服极限,可以满足可靠性与安全性要求。而在75 MPa和125 MPa内压作用时,均在瓶体上端结构与瓶体主结构连接位置处出现最大应力,且已超过材料的屈服极限,但由于塑性区域仅仅存在于倒角位置的表层,未能穿透整个气瓶壁面。因此根据塑性失效设计准则气瓶结构设计满足要求。
气瓶在50 MPa、75 MPa与125 MPa这3种内压载荷工况下,瓶体焊接区域的Mises应力最大值分别为370 MPa、555 MPa和925 MPa。
3 高压气瓶的爆破形态分析
G.拉梅基于弹性理论推导得到了气瓶瓶壁的三向应力计算公式,即周向应力σθ、径向应力σr和轴向应力σz。拉梅公式为高压气瓶的爆破形态分析提供了有效的方法。
3.1 瓶体爆破形态的理论分析
拉梅公式如式(3)所示。
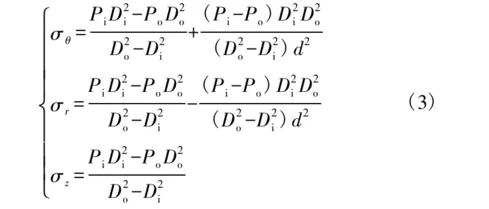
式中:Pi为瓶体内部压强;Po为外部压强,取Po=0;Di为瓶体内直径;Do为瓶体外直径;d为瓶体的任意直径。
式中:Pi为瓶体内部压强;Po为外部压强,取Po=0;Di为瓶体内直径;Do为瓶体外直径;d为瓶体的任意直径。
由式(3)可以得到,瓶体任意位置处的周向应力和径向应力的大小不仅仅与瓶体内外压强和内外直径有关,还受到具体位置的影响,而轴向应力仅与瓶体内外压强和内外半径有关。同时根据式(3)可以得到,同一位置处周向应力数值最大,轴向应力位于周向应力和径向应力两者之间,并且可以得到:
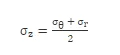
首先对气瓶在工作载荷作用下的应力情况进行理论分析,将Po=0、Di=50 mm和Do=57 mm带入式(3)得到三向应力计算式:
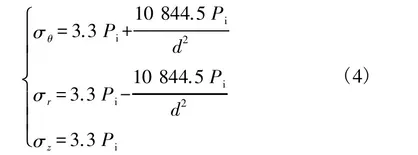
式(4)即为任意直径d处的三向应力与内部压强之间的关系,由于本文基于塑性失效设计准则,即瓶体在发生爆破时,要求瓶体某一部位整个壁面应力均达到屈服极限,即塑性区域穿透整个壁面。根据式(4)中周向应力计算式可以得到,瓶体内部材料在内压载荷作用下应力值较外部材料大,率先达到屈服极限,而随着内压载荷的增加塑性区域逐渐扩大,直至瓶体最外部材料也达到屈服极限,丧失继续承载能力,瓶体发生爆破失效。因此,取直径d=Do=57 mm,屈服强度σs=1 000 MPa带入式(4),可以得到瓶体爆破压强为
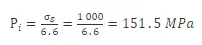
经过以上分析计算,可以得到瓶体在内压151.5 MPa工况时发生爆破,且理论爆破形式为周向撕裂状,与设计要求相同。
3.2 瓶体爆破形态的仿真验证
气瓶在继续加压的过程中,当内压达到152.4 MPa左右时,瓶壁整体出现了穿透壁面的整体塑性变形,瓶壁失去进一步的承载能力,如图8所示。Mises应力的最大值出现在气瓶瓶顶与瓶壁的弯折处,这将导致气瓶在此处出现与理论计算一致的横向撕裂裂口。上端结构与瓶体主结构连接处的Mises应力数值依然较高,约为1 196 MPa,但塑性区域分布未穿透整个瓶壁,此处仍可以继续承受载荷。焊缝连接区域如图9所示,Mises应力最大值为1 007 MPa,也已超过材料的屈服极限。

图8 瓶体剖面图

图9 焊接位置处剖面图(152.4 MPa)
以上仿真结果可以得到,气瓶瓶体在152.4 MPa内压作用时,瓶壁整体达到屈服极限,无法继续承受载荷,瓶体发生爆破。表1为理论结果与仿真计算的对比情况。
表1 理论与仿真计算对比情况
| 理论压力/MPa | 仿真压力/MPa | 误差/% |
| 151.5 | 152.4 | 0.59 |
根据表2可以得到,仿真结果与理论计算完全相同。
3.3 气瓶瓶体爆破试验
经过以上设计及仿真过程,同时考虑充放气嘴结构对实际瓶体爆破试验的影响,开展高压气瓶结构的爆破验证试验。
利用爆破耐压试验台开展瓶体爆破试验,试验流程如下:
1)通过试验台向瓶体内注入自来水,至瓶体内水压达到75MPa(1.5倍工作压力);
2)保压10min;
3)继续注入自来水进行加压至瓶体发生爆破。
加压过程如图10所示。
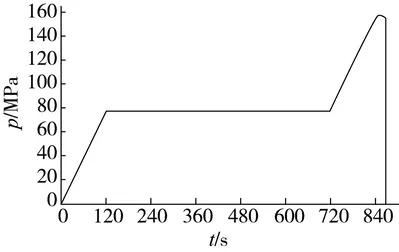
图10 加压过程
从加压曲线可以看出,当瓶体内压力达到75 MPa(1.5倍工作压力)后保压10 min过程中,压力稳定,表明瓶体的密封性和强度满足要求;当瓶体内压力达到某一值后,压力迅速降为0,表明瓶体已经发生破裂,压力释放。瓶体爆破后如图11所示。

图11 瓶体爆破图
根据瓶体爆破图可以得到,气瓶在高压载荷作用下发生爆破,爆破无碎片产生,爆破口成撕裂状,满足设计与安全性要求。
根据表2中4个气瓶的理论爆破载荷与试验的对比情况,可以得到实际瓶体爆破载荷与理论计算载荷基本相同,在考虑瓶体尺寸加工误差的允许范围之内,可以认为基于拉梅公式的爆破载荷分析方法是正确的。
表2 理论与实际爆破载荷对比情况
| 气瓶序号 | 理论压力/MPa | 试验压力/MPa | 误差/% |
| 1 | 151.5 | 154.14 | 1.74 |
| 2 | 151.5 | 155.00 | 2.31 |
| 3 | 151.5 | 155.02 | 2.32 |
| 4 | 151.5 | 154.86 | 2.22 |
4 结语
本文针对高压制冷气瓶的结构进行设计,应用ABAQUS 有限元分析软件对气瓶结构的3种载荷工况进行仿真试验。另外,基于拉梅公式对高压气瓶的爆破形态进行理论分析,并开展仿真与爆破试验进行验证,为高压气瓶产品的设计与分析提供一种快速、有效的方法。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删