形状记忆合金的本构模型构建与有限元仿真研究

序言：  

SMA本构模型是对SMA在不同温度下应力-应变关系的描述。不同于一般的工程材料，在不同环境下，SMA的力学性能差异很大，很难用一个统一的本构模型来表现其所有的力学行为。因此，需要根据SMA表现得主要力学特征，选择合适的、精度高的本构模型来描述SMA。

有针对性的开发SMA本构模型可以降低建模难度，提高计算精度和效率，易于工程推广。为了利用ABAQUS对SMA进行三维的仿真分析，许多学者进行了UMAT编程，将SMA三维本构嵌入ABAQUS中，实现了对SMA构件的有限元分析。常用的仿真软件ANSYS和ABAQUS中包含了SMA的本构模型，采用基于Auricchio的多线性简化模型，能简单仿真基本的超弹性性能，但无法模拟预应变以及复杂且精确的本构模型，于是许多学者对SMA的数值模型进行开发，如基于有限应变的Jaber三维SMA本构模型、Lagoudas的统一本构模型等等。

本贴先介绍了SMA的形状记忆效益和超弹性的相变与力学过程，然后采用分别采用ANSYS自带本构、ABAQUS自带本构、Jaber三维SMA本构模型的UMAT、Lagoudas统一本构模型的UMAT进行对比分析，最后针对不同仿真需求给出相应的SMA本构推荐。

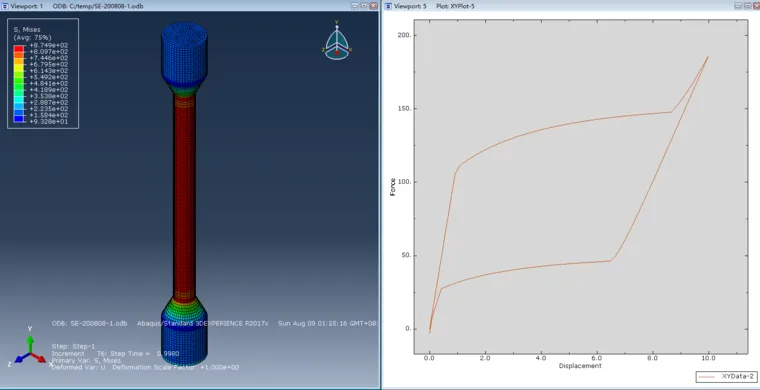
SMA是一类智能合金，具有多种特殊的性能。

SMA有两种主要的相：

一种是低温和高应力下稳定的马氏体相，另一种是在高温、低应力下稳定的奥氏体相。奥氏体相是SMA的母相，一般具有立方晶体结构。

马氏体具有较低的有序晶体结构按照晶向的不同存在两种形式：孪晶马氏体和非孪晶马氏体。图1-1为Ni-Ti SMA不同相的晶体结构示意图，图中的红点表示Ni原子，白点表示Ti原子。SMA的主要特征是马氏体与奥氏体之间的可逆相变，称为马氏体相变，这是由于剪切位移而改变晶体结构的切变型相变。这种相变可以由温度诱导，称为形状记忆效应。如果相变由应力诱导，则称为超弹性。

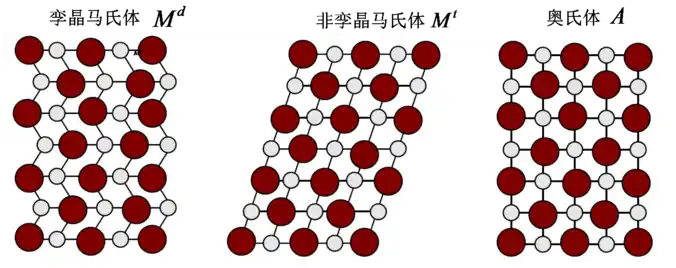
图1-1 SMA的不同相

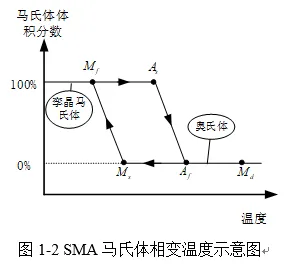
在无外应力的情况下，SMA中的马氏体体积分数随着温度而变化。

如图1-2所示，相变的特征温度有四种：

1)As ，即材料从孪晶马氏体相向奥氏体相转变的开始温度；

2）Af ，即材料从孪晶马氏体相向奥氏体相转变的完成温度；

3） Ms，即材料从奥氏体相向马氏体相转变的开始温度；

4）Mf ，即材料从奥氏体相向马氏体相转变的完成温度。这些转变温度会随着外应力的增加而升高。

形状记忆效应：指SMA经过热循环变形后，恢复其原始形状的能力。如图1-3所示，当温度低于Mf时，SMA处于孪晶马氏体相，再施加外力且高于临界应力时，向非孪晶马氏体相转变，卸载时保持该相。此时在加热SMA使之达到高于As时，会导致奥氏体相的形成，并恢复至其初始形状。在随后的冷却过程中，SMA转变为初始的孪晶马氏体相，残余变形消失。

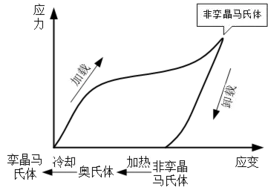
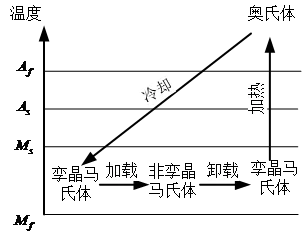
图1-3 形状记忆效应

超弹性：指在恒定温度下，由于应力诱导马氏体相变而产生的大应变的恢复。当温度高于Af时，SMA处于奥氏体相，施加足够高的应力时，SMA会发生应力诱导马氏体相变，转化为非孪晶马氏体相。

当荷载释放时，会发生逆马氏体相变，导致完全的变形恢复。超弹性的应力-应变曲线和温度示意图如图1-4所示。图中可见，当温度介于As 和 Af之间时，卸载时只有部分的变形恢复。而当温度高于马氏体相变的最高温度Md时，材料在奥氏体相下稳定，且无法发生应力诱导马氏体相变。在当温度介于Af和Md之间时，可以实现完全的变形恢复。

图1-4 SMA的超弹性效应

SMA的本构模型：

形状记忆合金的本构模型在过去的几十年里不断发展，已经从经验公式发展到全面的数学描述。目前可用的模型通过各种方法构造，从微观力学到统计物理和粒子动力学，再到经典塑性方法，再到结合热力学和能量守恒的方法。常见的有：微观热力学模型、微观-宏观模型和宏观模型。    

宏观模型主要基于唯象学、简化的微观-宏观热力学或者实验数据拟合来描述多晶SMA的行为。Tanaka和Nagaki建立了第一个用内部变量来描述单轴加载下SMA中的热塑性相变的宏观唯象模型，并由Tanaka扩展到指数变换硬化函数。

为了避免对不同相体积分数的明确限制，Liang和Rogers提出了一种基于马氏体体积分数 的余弦演化函数的三维模型，Brinson和Lammering将马氏体体积分数扩展为温度感应部分和应力感应部分。

Lagoudas等比较了指数和余弦模型的多项式方法，并用于模拟活性金属基复合材料的超弹性，与余弦模型和多项式模型相比，指数模型在预测应力-应变行为和热能-速率曲线方面不太令人满意。

Boyd和Lagoudas提出了第一种通过引入非弹性应变张量来解释马氏体再取向的模型，然而作者只关注比例加载，没有将数值结果与实验数据进行比较。SMAs的第一个三维唯象学模型归于Bertram。其他具有开创性的三维唯象学模型是Raniecki、Auricchio和Souza等人提出的。这些模型引领了SMA唯象学建模方面的重大进展。以下重点介绍Lagoudas的统一本构模型和Jaber的三维SMA本构模型。

SMA的有限元仿真：

常用的仿真软件ANSYS和ABAQUS中包含了SMA的本构模型，采用基于Auricchio的多线性简化模型，能简单仿真基本的超弹性性能，但无法模拟预应变以及复杂且精确的本构模型，于是许多学者对SMA的数值模型进行开发，如基于有限应变的Jaber三维SMA本构模型、Lagoudas的统一本构模型等等。

ANSYS:

在ANSYS自带的SMA本构模型中，采用四条折线模拟SMA的相变过程，，来模拟SMA的相变过程，该模型为基于Auricchio模型建立的简化模型，采用该本构模型模拟SMA的超弹性性能时，只需输入8个材料参数即可。

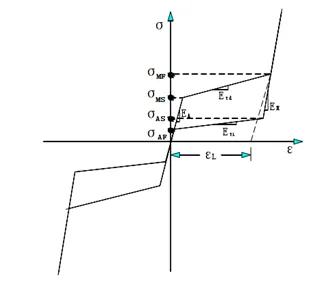
图 1-4  ANSYS中SMA的本构模型

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删