解决ABAQUS中橡胶大变形问题的有效方法

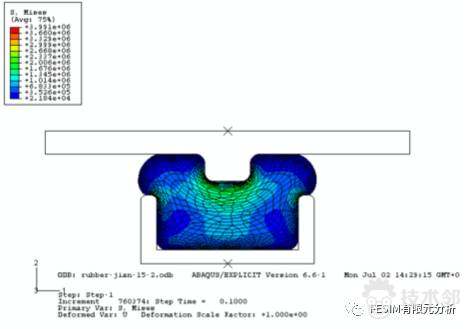
密封橡胶的数值仿真是一类典型的非线性问题，牵涉到材料非线性（超弹性）、边界非线性（接触）和几何非线性（大变形）问题的集合，如果设置不当，极容易导致求解困难。特别是在密封橡胶的变形复杂，比如和多个不规则边界接触、变形很大等情况，需要更谨慎的设置相关参数，以求得到合适的解答。

模型的适当简化

对薄板问题可忽略厚度方向的应力，作为平面应力（plane stress）问题；对长柱体可忽略第三方向的应变，作为平面应变（plane strain）问题;对O型圈等可作为轴对称问题。平面应力和平面应变在建立part时需选中2D Planar，轴对称问题需选中Axisymmetric；在选择单元时也应注意三者的区别（CPS* ,CPE*, CAX* ）。

求解器的选择

因为问题复杂，使用Standard求解容易不收敛，在精度允许的情况下，可选用Explicit求解器。只是多数时候Explicit求解时间较长。应当知道的是，对于橡胶这种典型的不可压缩材料，使用杂交单元（含字母H）是恰当的，但Explicit中没有杂交单元（庄茁书中的例子选用减缩单元）。并且在Explicit中，橡胶材料默认泊松比为0.475。

材料模型的选择

我只用过其中三个，Neo-hookean， 简单易用，就一个参数。对于初学者和简单的模拟比较方便。但是当变形增加到一定范围就不能得到准确的结果了，因为它的参数是来自小变形部分的应力-应变关系。Mooney-Rivlin 是比较常用的本构模型。对于没有加碳黑的橡胶来说，这模型能得到比较准确的结果。但是用它来模拟加了碳黑的橡胶就不太精确了。Yeoh 是用来模拟加碳黑后的橡胶，三个参数都比较容易得到。 可是这个模型在小变形 extension ration=1.5时结果不准确。另外，在橡胶材料模型中引入少量的可压缩性能够减少体积自锁。  

分析步的设置

多设置一个小载荷的分析步，让接触关系平稳的建立起来以后，在下一个分析步中施加更大的真实的载荷，可以减小收敛的困难。  

接触的设置

把刚体面或刚度较大的面作为主面，橡胶一般作为从面。刚性面上的尖角会引起收敛问题，可定义倒角光滑解析刚性面上的尖角。定义接触时应当注意接触面的法向方向应该相反。两个接触面之间滑动较大，故选用有限滑动算法。在ABAQUS/Standard中，对“Constraint enforcement method”的选择，平面应力问题建议选用“Node to surface”，平面应变问题建议选用“Surface to surface”。在结果出来后往往会发现出现穿透现象，这时需要重点检查两个方面：

1.接触定义是否正确，包括主从面、法线方向等；2.从面网格需要细化。

约束的设置

可能的情况下，应当增加约束，可以增大求解的成功的可能，而约束不足容易产生奇异解，比如橡胶“到处乱跑”。比如本模型中，可以对橡胶下方的接触点全约束，而橡胶上方的接触点只允许竖直方向的移动。

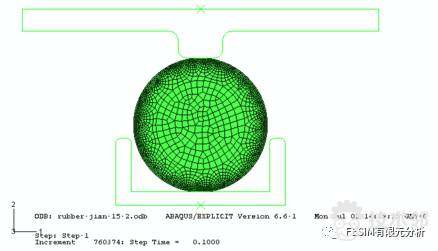
网格

网格的疏密、网格划分技术（Mesh controls）和单元类型的选择，对计算的成败影响很大。只能具体问题具体分析，可参考石亦平的《ABAQUS有限元分析实例详解》。划分好网格后最好使用verify来检查一下网格的质量，发生扭曲的地方要改善网格质量。变形严重的地方需要细化网格。优先选用线性单元，高阶单元容易发生单元畸变，易于导致计算失败和不准确的结果。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删