分析具有双重非线性特性的复杂钢结构节点的极限承载力

一、工程概况

本工程为某影城广场前的“大门”，建筑创意为电影的胶片-大飘带，建筑效果图如图1所示，结构设计采用MIDAS GEN 2020（V2.1）软件，结构采用钢结构片状桁架形式，如图2所示，端部采用V字型支撑整个结构体系，V字型支撑底部与基础连接，本文主要研究对象为V字型柱脚节点，该节点为关键受力部位，如图3所示。

图1  建筑效果图

图2  结构设计模型

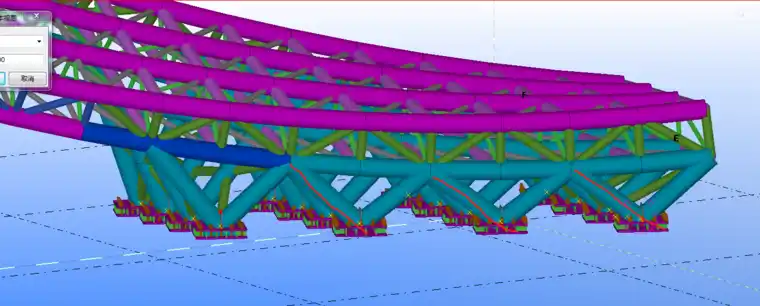
图3  V字型柱脚节点

二、有限元计算

2.1、节点几何模型

根据MIDAS Gen整体计算模型实际截取部位选取其中一个具有代表性且受力最大位置的节点进行有限元分析。支座2（节点844）由两根斜杆交汇形成一个“V”字型并汇交于底部钢板支座上，如图 4所示，节点的构造及各杆件几何关系、三维几何模型如图。

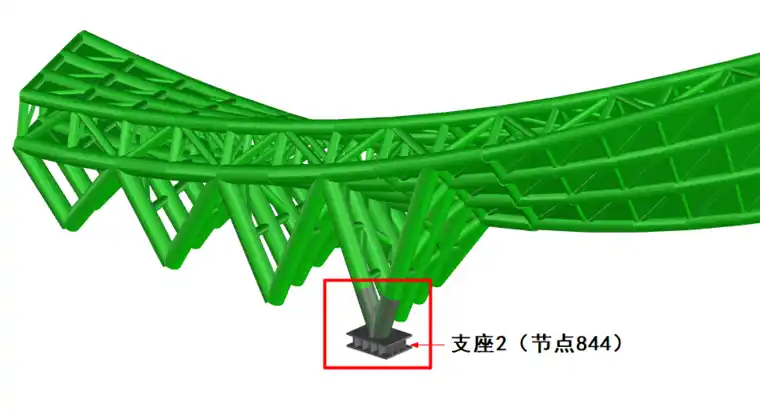
图 4 支座2（节点844）

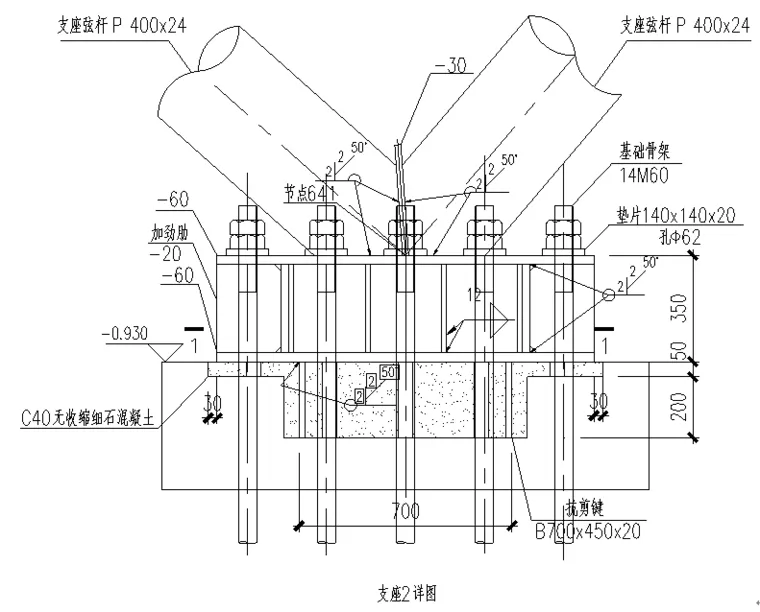
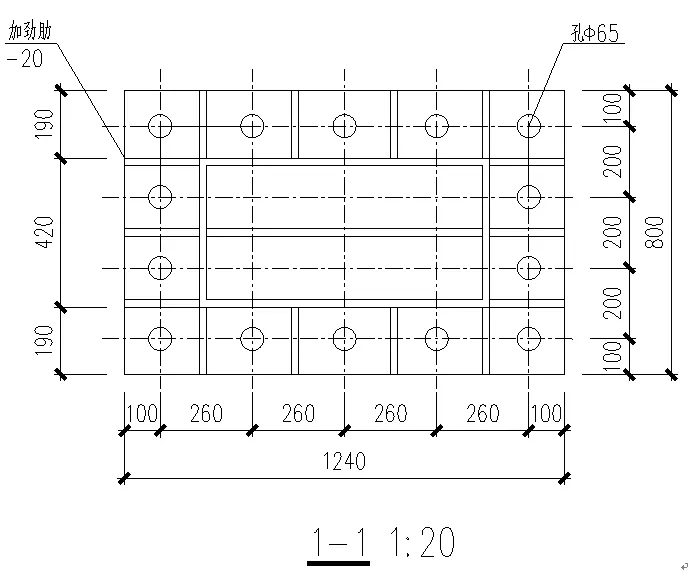
图 5 支座2节点平立面图及RHINO三维示意图

《钢结构设计标准》GB50017-2017中没有V字型柱脚节点的具体计算方法，对于此类特殊构造且传力关键部位的节点，需要进行有限元补充计算，在设计阶段通过MIDAS FEA软件建立节点的有限元模型，进行结构整体协同分析，检验节点处的设计安全性。节点作为结构整体的一部分，经常被剥离出来并进行边界简化，并从结构设计软件提取内力施加到节点有限元模型中去，再进行节点有限元计算分析，但边界条件假定会对结果产生一定的误差，工况较多，不便进行手动施加内力，故而采用MIDAS FEA进行节点与整体模型协同分析。后述并给出MIDAS FEA设计工况下的承载力分析结果。

审图专家认为本节点是关键的传力节点，需要进行极限承载力的验算，提出按照设计荷载的1.6倍来复核节点，以验证节点的安全系数。故本文采用ABAQUS软件中的弧长法加载的方式进行极限承载力的研究，计算过程中考虑了几何非线性和材料非线性。

2.2 、有限元模型

1）midas fea计算模型

钢管及板材采用三维实体单元模拟，单元形状为四面体；不考虑节点区域焊缝、螺栓连接对单元模拟的影响。为保证计算精度，划分网格时，单元尺寸取30~40mm。支座2（节点844）有限元网格划分如图6所示。

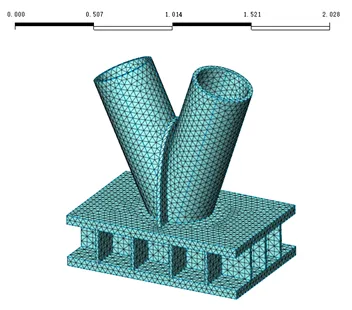
图6 支座2节点 MIDAS FEA有限元模型

2）ABAQUS计算模型  

采用四边形壳单元S4R模拟（S4R: A 4-node doubly curved thin or thick shell, reduced integration, hourglass control, finite membrane strains.）不考虑节点区域焊缝、螺栓连接对单元模拟的影响。图7为支座2节点有限元模型。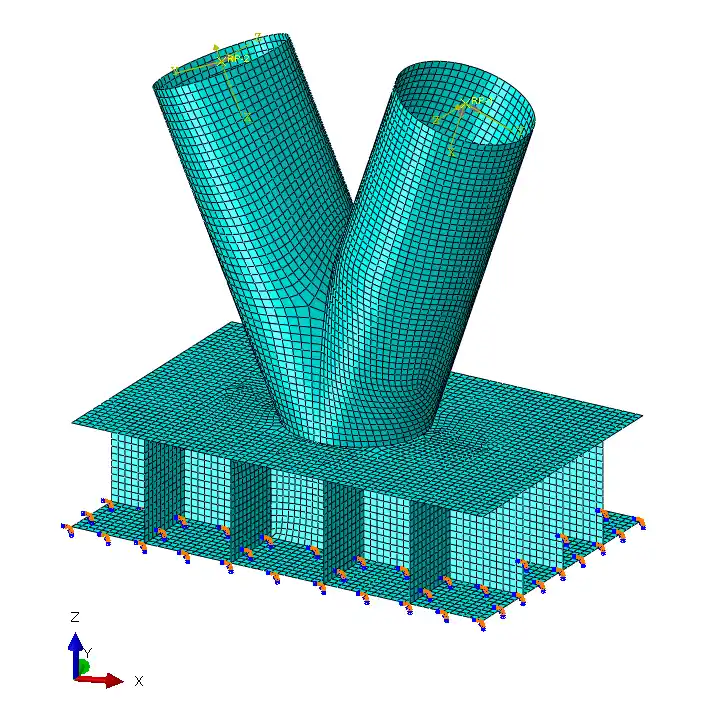

图7 支座2节点ABAQUS有限元模型

2.3 、材料本构模型

计算中采用的本构模型依次为：

1）钢材双线性随动强化本构

采用双线性随动硬化模型（如图8所示），考虑包辛格效应，钢材的应力-应变关系如图9所示，在循环过程中，无刚度退化。在多轴应力状态下，采用了Von Mises屈服准则判断钢材是否达到屈服。

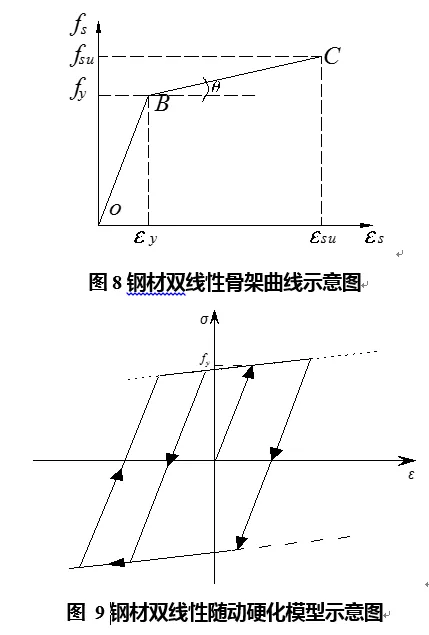
计算分析中，Q355钢屈服强度355Mpa，当470Mpa时假定对应的极限应变为0.015。

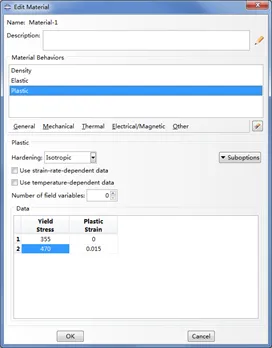
图10 ABAQUS材料参数输入

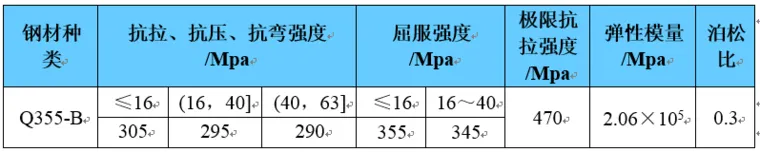
相贯节点的钢管及板材均采用Q355-B钢，材料参数如表 1所示，钢材的本构关系采用范梅塞斯(Von Mises)模型，不考虑钢材的硬化特性。

表 1 钢材材料参数表

2.4 荷载施加及边界条件

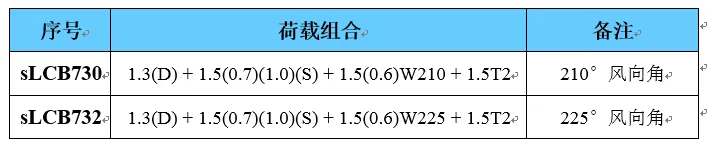
选取MIDAS GEN 整体模型中此节点处受力较大的荷载组合工况，表 2为最不利工况组合，表 3为荷载工况说明。

表 2 支座节点主要控制荷载工况

支座2（节点844）最不利工况内力：N = 2.4895e+006 N, My = -2.9235e+008 N*mm, Mz = 3.2967e+008 N*mm (sLCB730, J端)

表 3 荷载工况说明

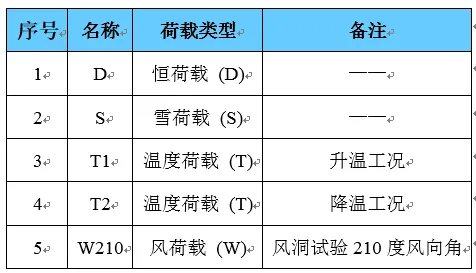
图11-12给出了设计最不利工况（sLCB730）下支座2（节点844）对应的荷载值施加，通过ABAQUS弧长法对节点进行分析，最终通过荷载比例系数曲线判定节点的极限承载力

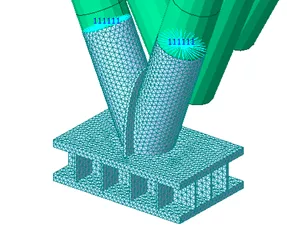
图11 Midas fea荷载及边界条件

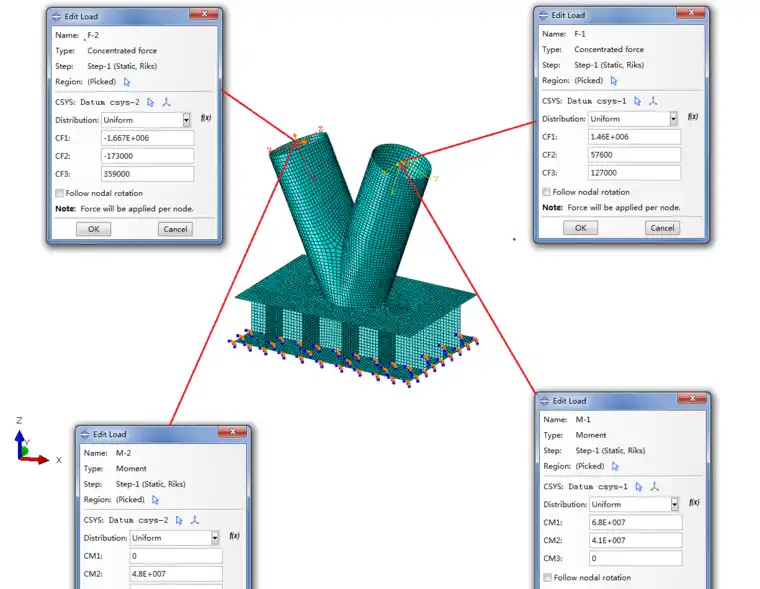
图12 ABAQUS荷载及边界条件

三、有限元计算结果

3.1、Midas fea设计荷载结果

图13给出了最不利工况（sLCB730）下支座2（节点844）对应的有限元计算结果，支座2最大的应力值为234Mpa，应力最大值出现在V字型与中间加劲板相交处，但应力值小于设计容许值290Mpa，满足设计要求。

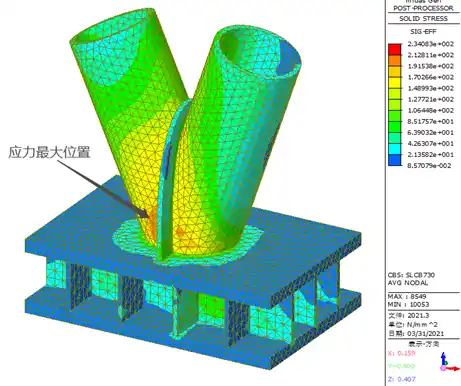
图13 Midas fea计算mises应力

审图专家认为本节点是关键的传力节点，需要进行极限承载力的验算，提出按照设计荷载的1.6倍来复核节点，以验证节点的安全系数。故本文采用ABAQUS软件中的弧长法加载的方式进行极限承载力的研究，计算过程中考虑了几何非线性和材料非线性。

3.2、abaqus节点极限承载力分析

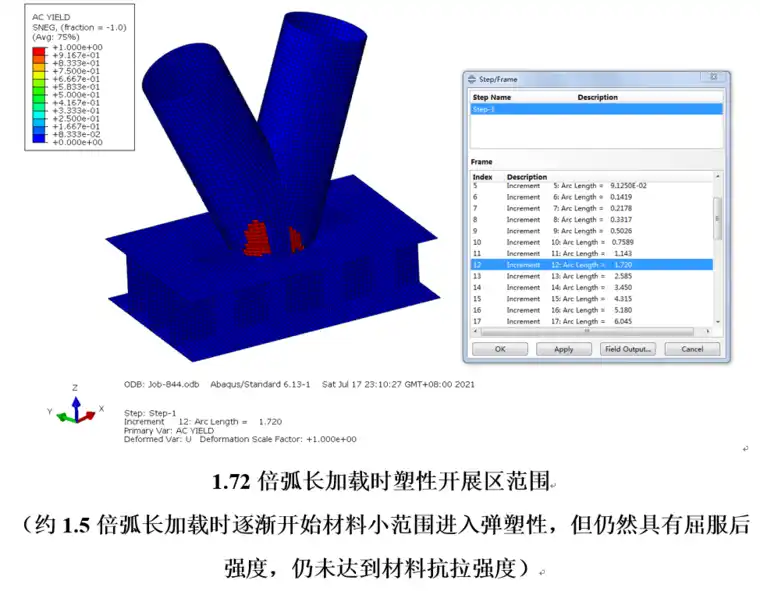
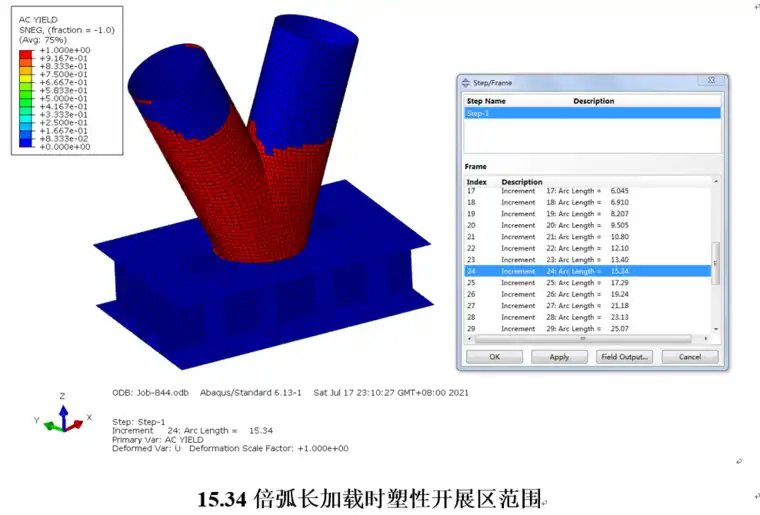
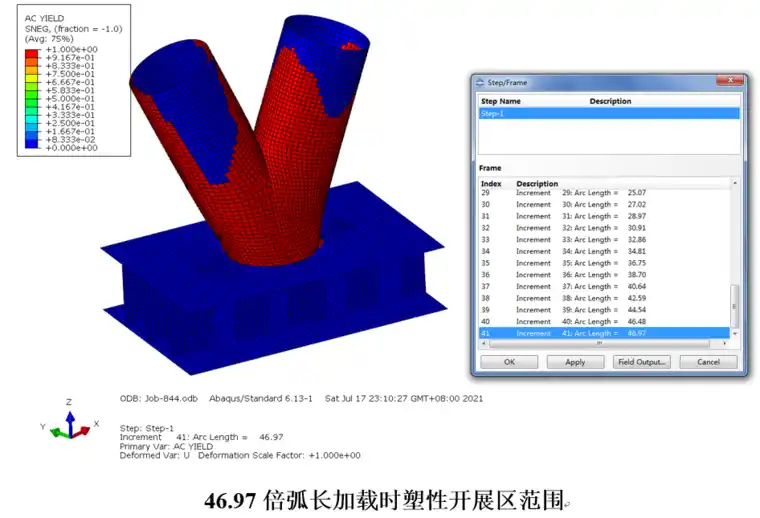
图14为基于弧长法极限承载力的加载研究，给出了逐步加载的过程节点的塑性开展过程及应力变化情况。

四、结论

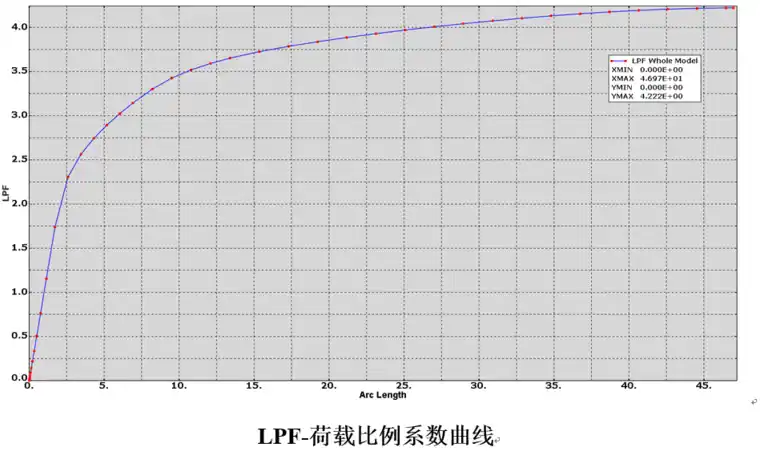
通过弧长法计算得出LPF荷载比例系数曲线，由图可知：

1）该节点的安全系数约为4.2倍设计荷载值

2）0.759倍弧长加载（约加载1倍设计荷载）时mises应力（最大值190Mpa）

3）1.143倍弧长加载时mises应力（最大值287Mpa）

4）1.72倍弧长加载时mises应力（应力最大值359Mpa，还远小于抗拉强度470Mpa），约1.5倍弧长加载时逐渐开始材料小范围进入弹塑性，但仍然具有屈服后强度，仍未达到材料抗拉强度

5）15.34倍弧长加载时mises应力（应力最大值470Mpa，已达到抗拉强度值）

6）46.97倍弧长加载时mises应力（应力最大值470Mpa，已达到抗拉强度值）

五、设备情况及计算耗时

1）计算设备：

2）计算耗时：约15min

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删