云南省昌宁至保山高速公路K79+560~K79+886高填路堤强夯段,设计行车速度80公里/小时,整体式路基宽度25.5米,分离式路基宽度12.75米。原为采空区,无组织回填。为避免已堆积填土的二次转运堆积,采用大能量强夯置换处置松填土方。该方法是将重力势能转换为冲击能及振动反复夯打地基土,从而提高地基土的承载力,降低地基土的压缩模量,拟在路基范围及坡脚外8m铺设1.5m片石层后采用强夯置换处理,消除12m深度范围内新填土变形,并形成硬壳层,增加地基承载力,减少路基沉降。
利用ABAQUS有限元软件,解决了夯击时大变形带来的网格畸变,以8000kN·m为例,对高能级强夯置换进行了详细的数值分析,得到了高能级强夯作用下的变形、应力及等效塑性应变,分析了高能级强夯置换的加固机理。
强夯置换法处理软土路基基层,一般先将地基土开挖至淤泥层的表面,接着在淤泥层表面抛填一定强度和厚度的片石形成工作垫层,在夯锤的作用下将片石夯入淤泥中,在夯坑中重复填料并夯击直至达到收锤标准,最终在淤泥层中形成置换墩,达到与墩间土共同承担上部荷载的目的。总的来说,强夯置换法加固地基的机理主要包括三个方面,即动力密实、动力固结和动力置换。
1) 动力密实
土是由固相、液相和气相组成的三项体系,土体的承载力主要由土颗粒之间相互接触形成的骨架承担,骨架之间的孔隙部分由气体和水来回填。强夯法在加固多孔隙、粗颗粒非饱和土的过程主要是动力密实的机理,夯锤的夯击能在土体中以波的形式扩散,使得土中的孔隙减小,孔隙中的气体排出,孔隙水压力增大,土颗粒产生相对位移和重排列,最终使得夯击范围内土体变得更加密实,达到夯实加固的目的。
2) 动力固结
动力固结作用主要针对细颗粒饱和土体。夯锤的冲击荷载会在土体中产生很大的应力波,扩散的应力波会使土体颗粒发生扰动,结构破坏,甚至局部液化并产生裂隙,这些新形成的裂隙相当于在土体中增加了排水通道,使得孔隙水排出,孔隙水压力得以释放,最终达到土体固结、提高强度的目的。在强夯置换处理软土地基的过程中,一方面夯锤瞬时强大的夯击能使得土体发生了动力固结,另一方面置换形成的置换体加速了固结排水的过程,使得地基强度可以有明显提高,这也是强夯置换法可以应用在高饱和度、高压缩性的软土地基处理的主要原因。
3) 动力置换
动力置换主要有整体置换和桩式置换两种方式。其中整体置换类似换土垫层,它是通过强夯将大块径的石渣、块石等相对强度较高的散体材料整体挤入待处理土层,凭借夯锤夯击产生的巨大冲击力将低强度、高压缩性的待处理土层挤开,最终在整平抛石层之后形成高密实度、低压缩性、力学强度好、承载能力强的工作垫层,达到整体置换的目的。
桩式置换是按照一定的夯点布置方式和夯点间距将石渣、块石等相对强度较高的散体材料夯入待处理土层,形成一些列规则排列的置换墩(或桩),处理后的土层与置换墩(或桩)一起形成复合地基。在软弱土层不是特别厚的情况下,桩式置换形成的置换墩会穿过软弱土层直达下部的持力层,由于置换墩材料相对于软弱土层来说压缩模量要大很多,处理后的地基在受力过程中会承担大部分荷载,墩间的软弱土的沉降变形量得以减小。当软弱土层厚度很大的时候,置换墩与墩间的软弱土层依靠侧向摩擦和内摩擦的共同作用承载上部荷载,并在强夯过程中形成硬壳层,并对上部荷载有扩散作用,也可以达到提高地基强度的目的。
1) 工程地质概况及土层参数的选取
该地区地貌单元属构造侵蚀丘岗地貌。桥梁为跨越当地清水沟煤矿一处采坑区而设;现状地势较开阔,整体地形起伏不大,桥址附近周边为种植坡地;地形坡度约 5~10°,地面标高在 1621.80~1632.40m 之间。场区为废弃的人工采煤坑洼地;由于采煤后地势较低,周边降水汇集于此,形成一水塘(现已回填 )。
根据工程地质测绘及钻探揭露,桥址区地层主要为施工填土、采矿回填的素填土、、炭质泥岩、全风化泥岩(Q4)。人工填土(Q4ml):杂色,松散,主要以粘性土及片石为主,为路基工程填筑土,该层为本工程施工回填渣土,土质较疏松,揭露厚度为 1.0~16.0m 左右。平均指标:土体密度1850kg/m3,压缩模量6MPa,泊松比0.36,黏聚力25kPa,摩擦角15°;素填土(Q4ml):灰色、灰黄色、黑色,湿。在水塘内,该层土体受水浸泡后,岩芯较软,手指可按得动。该层土质主要由采煤开挖后的弃土和矿渣组成。根据走访,因采煤该层土体经人工多次翻动搬运,土质疏松。根据试验结果,该层土孔隙比大,压缩性较高,为中压缩性土。
该层覆盖于煤坑地表,揭露厚度 4.5~25m。平均指标:土体密度1850kg/m3,压缩模量6MPa,泊松比0.36,黏聚力25kPa,摩擦角15°;炭质页岩(N2):灰黑色,泥炭质,薄层理或片状构造,裂隙发育,岩质极软,经机械破碎多呈砂状和角砾状及少量岩夹土状,污手,采取率为 80 ,揭露厚度 7.00~12.00m。平均指标:土体密度1950kg/m3,压缩模量20MPa,泊松比0.3,黏聚力50kPa,摩擦角18°。;全风化泥岩(N2):灰黑色,炭质,原岩已完全风化,岩芯呈可塑土状,局部夹有强风化碎块,采取率为 85 。岩质较软,遇水易散解,揭露厚度 10.00~22.20m。平均指标:土体密度1950kg/m3,压缩模量20MPa,泊松比0.3,黏聚力50kPa,摩擦角18°。土层分布如图2-1所示。
该工程在路基范围及坡脚外12m铺设1.5m片石层后采用强夯处置,片石层平均指标:片石层密度1850kg/m3 土体密度1950kg/m3,压缩模量30MPa,泊松比0.23,屈服强度1.2MPa,摩擦角37.5°。

图2-1 地层分布
2) 计算模型建立
图2-2为计算采用1/4对称三维模型, 计算土体平面尺寸为20ⅹ20m,深度方向取30m;在保证计算精度前提下提高分析效率,对夯锤中心点半径4米内网格加密,加密区网格尺寸0.33ⅹ0.75m;土体采用Mohr-Coulomb本构模型模拟,片石层为理想弹塑性模型;模型竖向外侧固定水平位移;内侧竖向对称面采用轴对称边界,土层底部固定竖向和水平位移。截取地基模型尺寸够大,可忽略边界反射波对强夯置换计算精度的影响。

图2-2 计算模型
夯击初始参数取夯锤直径2.5m,锤重34.2t,落距24.3m,夯击能量8000kN·m时,对夯锤下部倒圆角,避免应力集中引起网格畸变过大;将夯击过程等效为具有一定初速度夯锤对土体的冲击作用。由于片石为散粒体结构,夯击过程只将夯锤下部片石夯入土体,夯锤与片石、片石与填土接触方式采用法向“硬接触”、横向无摩擦,接触时间为0.2s。
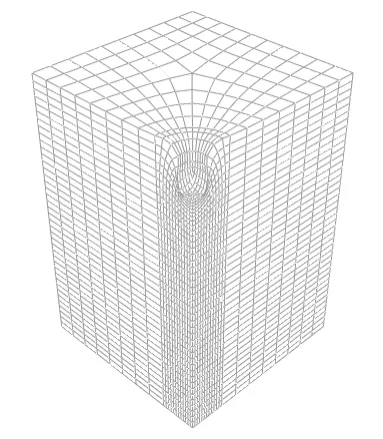
图2-3 ALE自适应网格
为避免连续夯击过程中网格畸变过大,采用ABAQUS提供的自适应网格划分技术(Arbitrary Lagrange-Euler Method,简称ALE),该方法可适用于强夯施工模拟。ALE方法结合了纯拉格朗日分析和纯欧拉分析的优点。
如图2-3,夯击过程中为适应土体极大变形,避免网格畸变,在夯点中心半径4米范围内网格大变形区域采用ALE网格划分,在计算时每个增量步进行一次扫掠,检查是否存在网格畸变并进行网格重新划分,生成新网格后将旧网格中应力、应变位移等变量传输到新网格上。通过上述方法,网格与物质点相互脱离,网格发生大幅度扭曲变形,以适应夯坑形状。
3.1 模型验证
1) 土体变形分析
以夯坑深度和夯沉量作为反映强夯置换加固效果的主要物理量,夯坑深度为土体竖向变形,夯沉量为夯击作用面的竖向位移。以8000kN·m强夯能级为例,本小节分析了在高能级强夯置换作用下的夯坑变形规律、夯沉量变化、计算区域内竖向位移分布及分次夯击后土体分布规律,并与实测数据相比较,以验证本文建立模型计算的可行性与正确性,在此基础上探讨高能级强夯置换作用下土体变形特征。
图2-4为8000kN·m能级时不同击数土体变形图。经过第1击时中心1.3m半径范围内出现夯坑,中心点夯沉量0.80m,夯坑边缘夯沉量略高为0.82m,夯坑外侧0.5m宽度范围内地表略有隆起;片石在夯击过程中发生侧向挤压,夯坑尺寸略大于夯锤直径2.5m,对比第2、3、5和9击过后夯坑变形曲线,可以发现前3次夯坑形状较为相似,夯坑深度随击数增加而增大,夯坑外侧地表隆起范围略有增加,侧向挤压作用更加明显;向夯坑内回填1/3至1/2深度片石后,第5击夯坑深度继续增大且片石的侧向挤压作用显著,经过全部9次夯击后夯坑最终呈鼓状,体现了片石的挤淤置换作用。
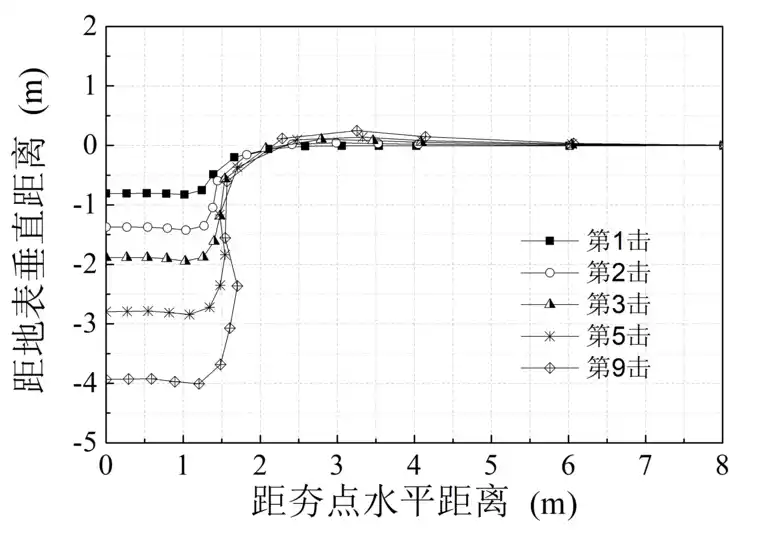
图2-4 8000kN·m能级不同击数夯坑变形图
2)片石置换墩分析
在强夯置换所形成的复合地基中片石墩墩体直径和长度是影响地基加固效果的关键因素,本节内容研究在8000kN·m能级强夯置换作用下形成的置换墩长度、半径等,分析强夯置换复合地基的置换加固效果。
从图2-2中可以得出,经过全部9次夯击后夯坑直径2.6m,土体竖向变形4.14m;回填碎石至起夯面后置换墩长5.64m,呈鼓状,在深度1.5m~3m处墩体发生侧向挤压,这是因为回填1.2m片石后,在夯击作用下片石向侧向挤压变形,最终形成鼓状墩;另外,在片石挤压置换作用下,夯坑直径略大于夯锤直径2.5m。分析得出8000kN·m强夯置换形成置换墩直径1.6m、长度5.64m。
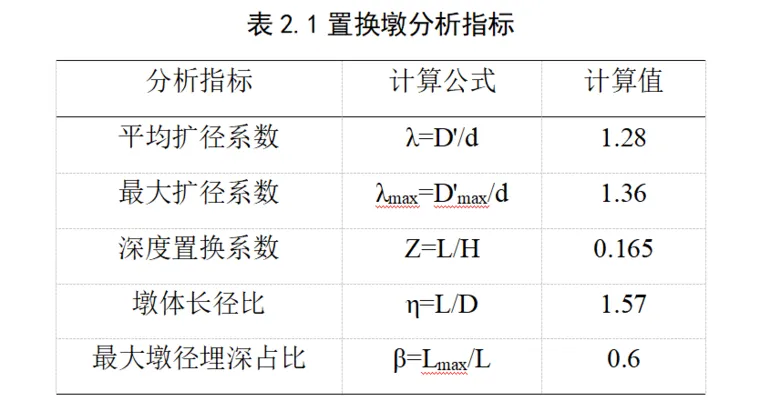
注:D为锤径,D'为单墩深度内平均置换墩径,D'max为单墩最大墩径,L为置换墩长,H为落距,η为墩体长径比,Lmax为最大墩径埋深。
强夯置换完成后,夯坑总体积约29.76m3。经过第1击时夯坑体积约4.3m3、直径约1.3m,占总体积14.4%;经过第2、3击时夯坑体积快速发展,直径分别为1.4m、1.48m,夯坑体积增量占比分别为14.6%、18.5% 。可以看出,在前3击后片石向两侧挤压,夯坑直径不断扩大,夯坑体积也随之增大。第5、9击后夯坑体积增量占比分别为17.8%、16.9%,在夯击作用下土体逐渐压密,强度不断增大,夯坑体积增量随之减小,直至稳定状态。
3) 夯沉量随击数的变化
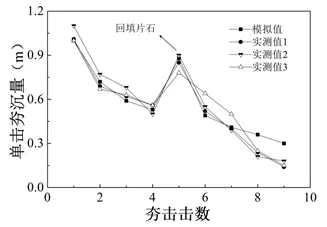
图2-5 8000kN·m能级单击夯沉量与夯击次数关系曲线
图2-5给出了8000kN·m能级单击夯沉量与夯击次数相关关系。可以看出,模拟值与实测值单击夯沉量发展趋势基本相同;模拟值中前4次夯击单击夯沉量分别为0.99m、0.73m、0.58m和0.52m,单击夯沉量差值逐渐减小。第1击时土体最为松散且夯沉量最大,土体发生显著压缩变形,单击夯沉量差值随夯次增加而逐渐减小。向夯坑内回填1/3~1/2夯坑深度片石后,首次夯击(即第5次)夯沉量恢复至0.59m,这是因为回填松散片石后,在夯击作用下被压密;另外,回填片石后置换作用增强,片石向两侧挤压变形显著;回填片石后单击夯沉量快速衰减,最终两击夯沉量为0.25m和0.23m,夯坑内变形趋于稳定。对比三组现场强夯置换实测数据,模拟值与实测值呈现一致的变化规律且拟合度较高。
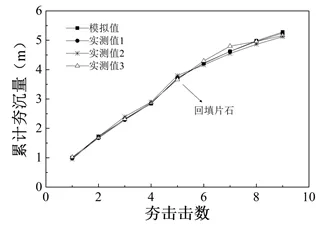
图2-6 能级8000kN·m时击数与累计夯沉量变化曲线
图2-6为能级8000kN·m时击数与累计夯沉量变化曲线,累计夯沉量随着夯击次数增加而增大,增长趋势逐渐减缓;回填片石后夯沉量加速衰减,最终趋于稳定。最佳夯击数为8~10击,不仅能够满足地基的加固要求,也能有效地利用夯击能量;通过与实测数据的比较,证明本计算方法可以有效地模拟高能级强夯置换的作用过程。
4) 强夯置换有效加固范围
在巨大冲击荷载作用下,夯点处大面积土体发生塑性变形,该值大于0.1则土体材料已经屈服并处于压密状态。图2-7为不同击数下有效加固范围。如图a经过第1击时,可以有效加固深度0~5.8m,径向0~3m范围内土体,随着夯击次数的增加,有效加固范围不断扩大,其增长幅度不断减小,在第9击完成后,可以有效加固起夯面下深度0~11.6m,径向0~4米范围内土体,达到该工程设计要求。前3次夯击有效加固范围形状较为相似,向夯坑内回填1/3至1/2深度片石后,第5击回填片石区等效塑性应变区半径不断增大,片石侧向挤压作用更加显著,有效加固半径大于夯坑底部。
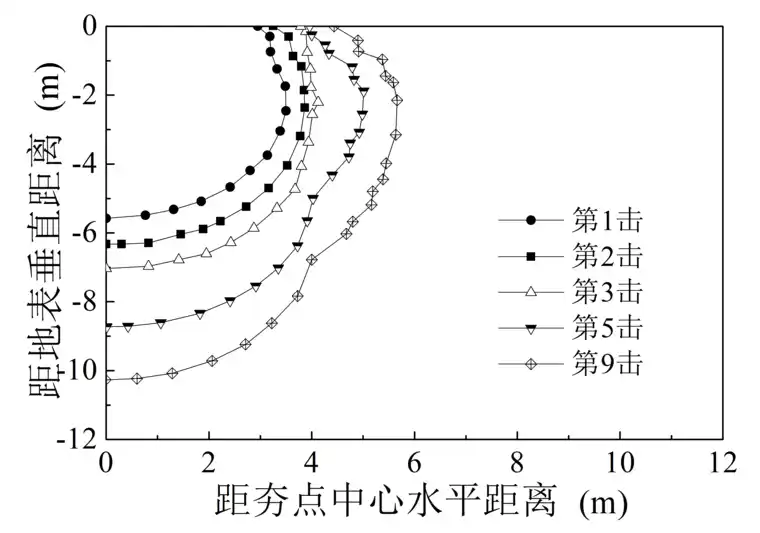
a) 0.1%等效塑性应变区
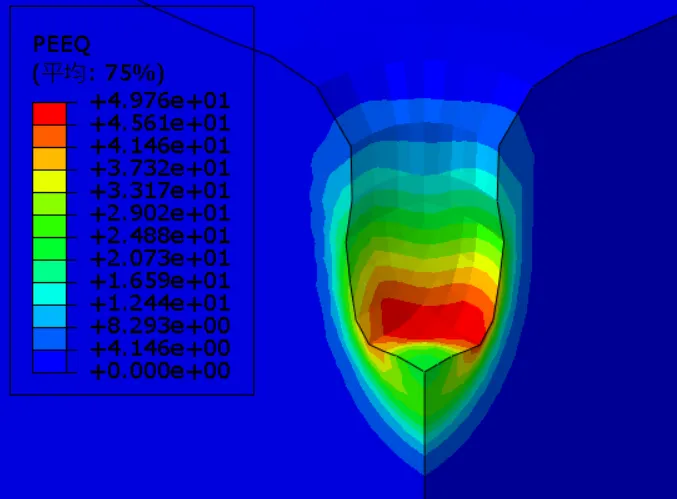
b)第9击等效塑性应变云图
图2-7 8000kN·m时不同击数下有效加固范围
5)强夯置换应力分析
首先从每一次夯击完成后土体竖向应力和水平应力分布云图出发,直观地了解在8000kN·m高能级强夯置换作用下,影响区域内土体应力分布的总体形态,研究了在各次夯击后,中心点处土体的竖向应力随深度的变化规律,分析各次夯击的作用效果。
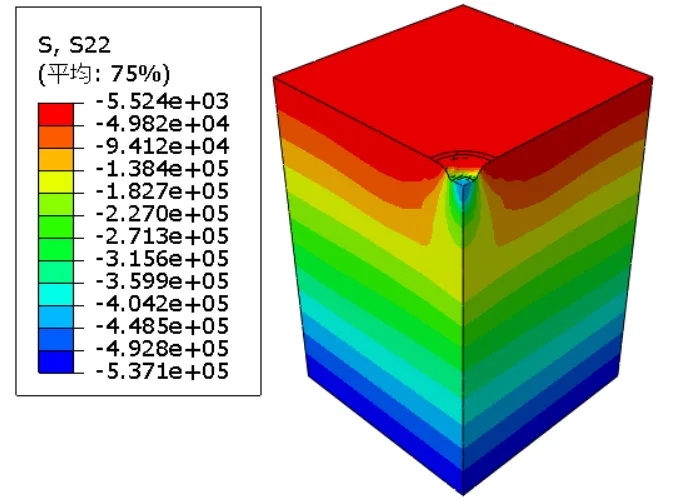
图2-8 第1击时竖向应力沿深度分布云图
图2-8为第1击时竖向应力沿深度分布云图。经过第1击后,夯锤边角处发生应力集中,锤底的应力分布为中心小边缘大;在强夯影响区域内,土体的应力变化较为复杂,总体呈现出从最大应力点向四周不规则递减的规律;在强夯影响区域外,土体的竖向应力为自重应力,呈条形分布,随着深度线性增长。;图2-9夯点中心竖向应力沿深度分布,可以发现,在各次夯击作用下,竖向应力的分布变化形态基本一致:最大应力发生在锤下一定深度处,并随着夯坑深度的增大,最大应力点发生的深度也在变化。在第1、2、3、5和9击夯击完成后,最大应力点至锤底的距离分别为0.6m、0.8m、1.05m、0.9m、1.6m,可以发现,随着夯击的进行,最大应力点至锤底的距离越来越大,最大应力值分别为0.44MPa、0.53MPa、0.55MPa、0.56MPa、1.1MPa,这是由于夯击后,锤下一定深度范围内的土体发生了反弹,从而使应力得到部分释放。另外,当夯击产生的应力与地应力相等时,从起夯面到该点的距离为强夯的影响深度,则第1击影响深度10.5米,大于有效加固深度8m;有效加固深度和影响深度随着击数的增大不断增大,经过全部9次夯击后有效加固深度为13m,影响深度为13.5m。
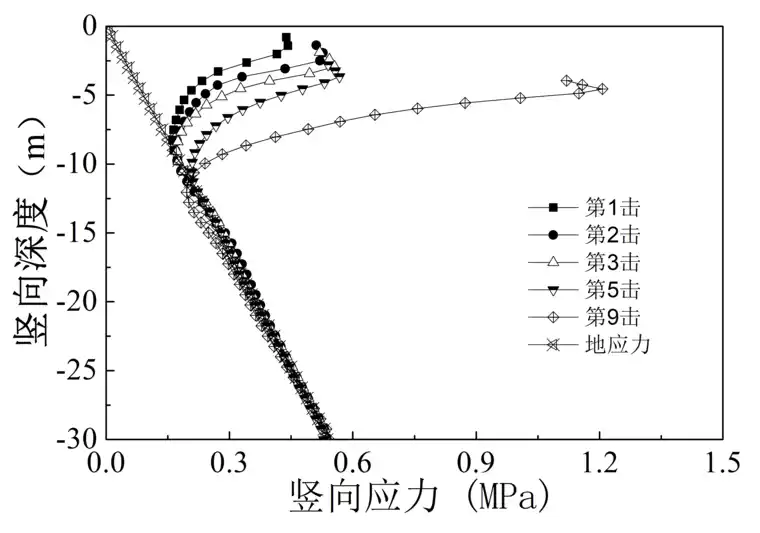
图2-9 夯点中心竖向应力沿深度分布
6)小结
通过计算分析8000kN·m高能级强夯置换(夯锤直径2.5m)作用下的夯沉量、土体变形、应力和塑性应变。
1)随着击数的增加夯沉量不断增大,最终逐渐稳定;在夯坑外侧土体略有隆起,隆起范围随着夯击次数增加不断增大。
2)当土体等效塑性应变大于0.1时认为土体被有效加固,随着击数的增加等效塑性应变峰值不断增大,有效加固深度也随之增大,但增长的幅度不断减小。
3)夯击作用完成后竖向应力的最大应力点出现在锤下1.5m~2.5m深度处;随着击数增加,最大竖向应力不断增大,且增长速度越来越慢。
4)经过全部9次夯击后,8000kN·m强夯置换有效加固深度13m、有效加固宽度4m,并确定最佳击数为8~9次。
3.2 强夯置换机理分析
在强夯置换的设计施工中,土质条件是一个关键参数,由于现场土层不均匀分布,深软杂填土厚度变化对强夯置换效果产生极大影响。本节内容研究在能级相同,锤重和落距也相同的条件下,调整土层厚度分布,从夯沉量、夯坑变形、有效加固深度和水平加固宽度来分析高能级强夯的加固效果,夯沉量包括单击和累计夯沉量,加固效果从土体等效塑性应变分布来考虑。
1)计算模型及参数选取
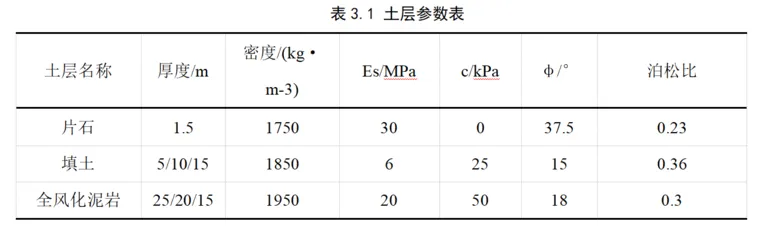
为了研究深软杂填土厚度对高能级强夯加固效果的影响,分析了深软杂填土5m、10m、15m、30m厚时,夯击能量8000kN·m,夯锤重34.2t,落距24.3m的三种工况。计算采用1/4三维对称模型,模型径向取20ⅹ20m,深度取30m,网格尺寸0.33ⅹ0.75m,网格总数8800个。土体本构模型采用Mohr-Coulomb模型,片石本构模型采用理想弹塑性模型,土层参数如表3.1所示。
2) 深软杂填土厚度变化时的夯沉量
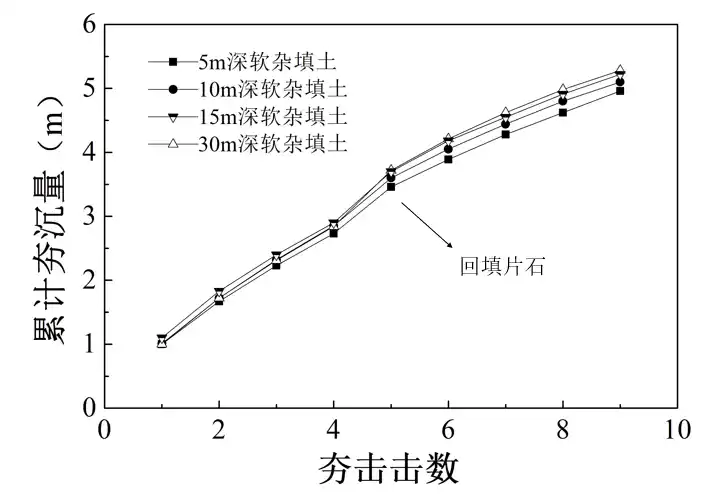
图3-1 累计夯沉量与击数的关系
图3-1为深软杂填土厚度变化时累计夯沉量与击数的关系。可以看出,不同深软杂填土厚度的累计夯沉量均随着击数的增加而增加,经过全部9次夯击后累计夯沉量分别为4.96m、5.1m、5.22m、5.28m,可以看出,深软杂填土越厚,总夯沉量越大,最大夯沉量差值0.32m。

图3-2 单击夯沉量与击数的关系
图3-2为深软杂填土厚度变化时单击夯沉量。可以看出,前4次夯击随着击数的增加单击夯沉量越来越小,在回填片石后夯沉量显著增大,随后夯沉量不断减小并趋于稳定;这表明在夯击作用下片石被压密及侧向扩出的变形过程。经过第1击,各深软杂填土厚度的夯沉量差别不大,约1m;经过第2击,单击夯沉量分别为0.67m、0.71m、0.73m、0.72m,深软杂填土5m厚时单击夯沉量明显减小,这是因为下部全风化泥岩距离地表较近,土体强度高。另外,当深软杂填土15m厚时总夯沉量与30m厚时差别不大,深软杂填土厚度超过强夯置换有效加固范围,总夯沉量基本不变。
3) 深软杂填土厚度变化时强夯置换的有效加固范围
a) 5m深软杂填土
(b) 10m深软杂填土
(c) 15m深软杂填土
(d) 30m深软杂填土
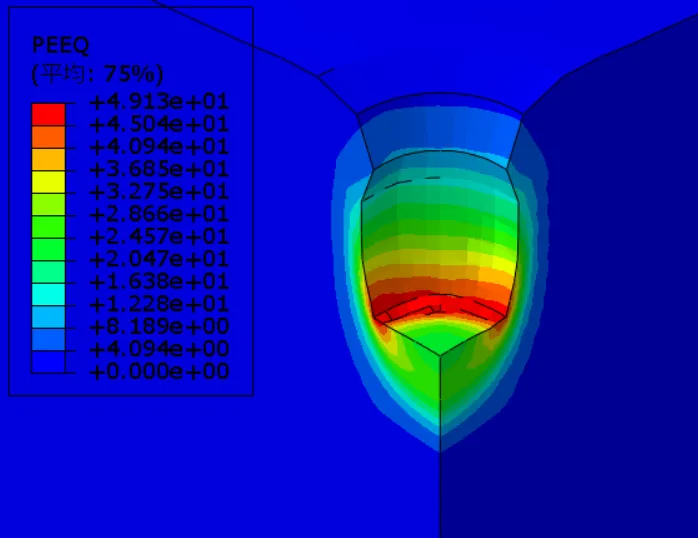
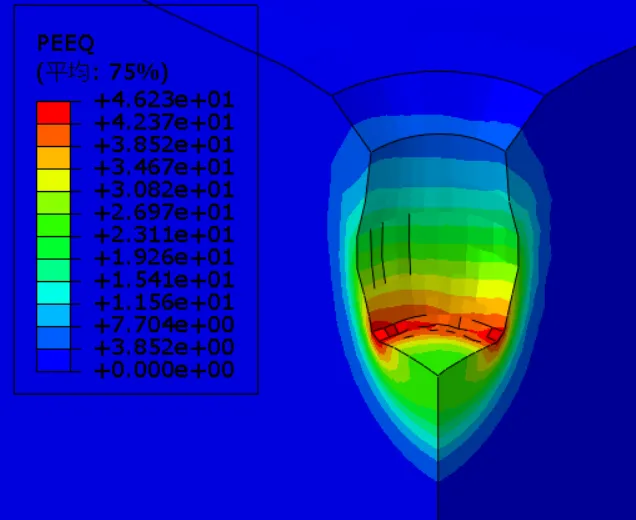
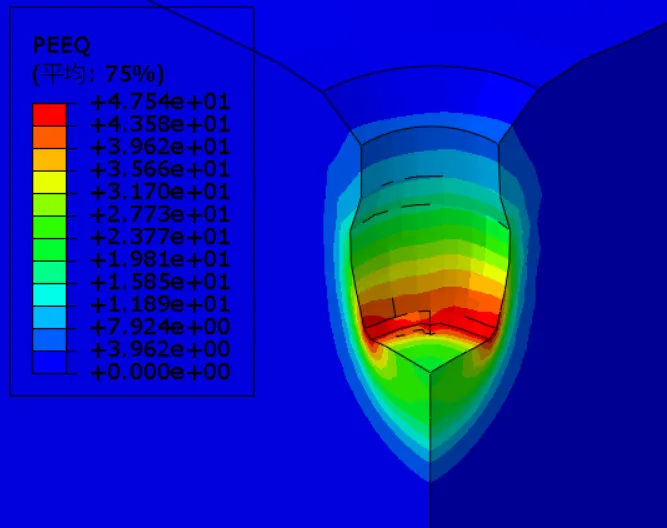
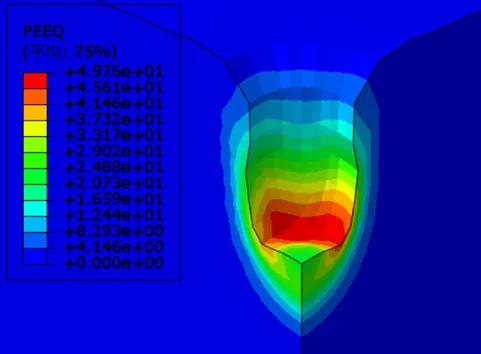
图3-3 不同土层下等效塑性应变云图
图3-3为不同土层下等效塑性应变云图,当深软杂填土5m、10m、15m和30m厚时等效塑性应变峰值分别为49%、46%、47%、50%,可以看出,深软杂填土厚度发生变化时,土体等效塑性应变峰值变化较小;强夯置换有效加固半径基本不变,均4m左右;当深软杂填土5m、10m、15m和30m厚时有效加固深度分别为11.6m、12.4.m、12.8m、13m,随着深软杂填土厚度增大,强夯置换有效加固深度不断增大,有效加固深度的差值不断减小。

图3-4 置换墩形状
图3-4为不同深软杂填土厚度下置换墩形状,曲线左上一侧为片石层,右下一侧为土层。当深软杂填土5m、10m、15m和30m厚时置换墩长度分别为5.09m、5.39m、5.45m、5.53m,可以看出,随着深软杂填土厚度的增加,置换墩长度逐渐增大,而深软杂填土厚度超出强夯置换有效加固范围时,置换墩长度稳定于5.5m。
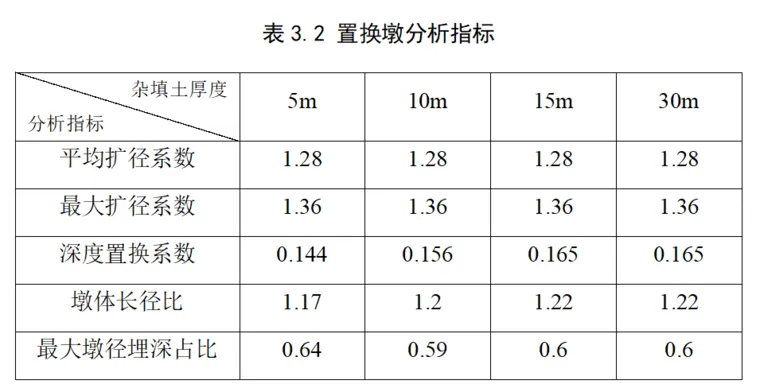
因此在该强夯置换工艺条件下,能够适应各种地层变化,能够有效加固12米深、4m宽深软杂填土。
3.2 夯锤底面积变化对加固效果的影响
在强夯置换的设计施工中,锤底面积是一个极为重要的参数。相同能级作用下,不同的锤底面积直接影响强夯施工的加固效果。本节内容研究在能级相同,锤重和落距也相同的条件下,调整锤底面积,从夯沉量、有效加固深度和水平影响宽度来分析高能级强夯的加固效果,夯沉量包括单击和累计夯沉量,加固效果从土体等效塑性应变分布来考虑。
(1) 计算模型及参数选取
为了研究锤底面积对高能级强夯加固效果的影响,分析了夯锤底面直径分别为3m、2.5m、2.2m和1.8m时,夯击能量8000kN·m,夯锤重34.2t,落距24.3m的四种工况,各工况的土层参数相同,土质参数如表3.2所示。计算采用1/4三维对称模型,模型径向取20ⅹ20m,深度取30m,网格尺寸0.33ⅹ0.75m,网格总数8800个。土体本构模型采用Mohr-Coulomb模型,片石本构模型采用理想弹塑性模型。
边界条件:模型竖向外侧固定水平位移;内侧竖向对称面采用轴对称边界;在土层底部固定竖向和水平向的位移。
荷载的施加:当夯锤底面直径分别为3m、2.5m、2.2m、1.8m、1.5m和1.2m时,为保证夯锤质量不发生变化,夯锤高度分别为0.57m、0.82m、1.06m、1.58m,夯锤初速度22.2m/s。
(2) 锤底面积变化时的夯沉量
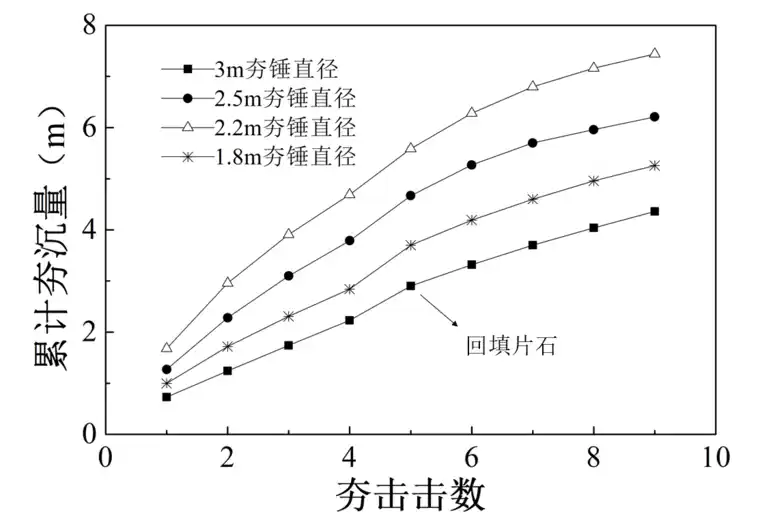
图3-5 锤底面积变化时累计夯沉量与击数的关系
图3-5为锤底面积变化时累计夯沉量与击数的关系。可以看出,不同夯锤直径的累计夯沉量均随着击数的增加而增加且不同直径的累计夯沉量之间的差值也越来越大。经过全部9次夯击后累计夯沉量分别为4.36m、5.26m、6.21m、7.44m,直径1.8m的夯锤面积比直径2.2m、2.5m、3m分别小了33%、48%、64%,最终沉降量分别大20%、41%、71%。可以看出,夯锤底面积越小,夯击能越集中,总夯沉量越大。
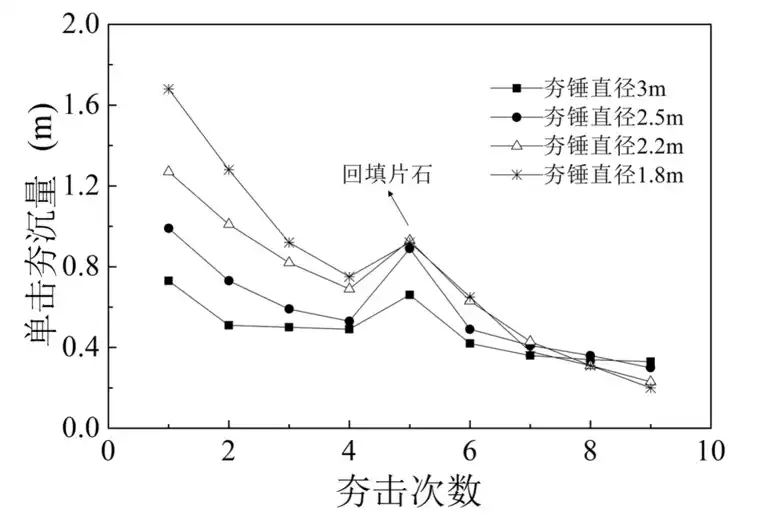
图3-6 锤底面积变化时单击夯沉量
图3-6为锤底面积变化时单击夯沉量关系。可以看出,前4次夯击随着击数的增加单击夯沉量越来越少,在回填片石后夯沉量显著增大,随后夯沉量不断减小。经过第1击时,夯沉量分别为0.73m、1m、1.27m、1.68m,直径1.8m的首击夯沉量最大,比直径2.2m、2.5m、3m的首击夯沉量分别提高32%、70%、138%;经过第2击时,单击夯沉量分别为0.51m、0.73m、1.01m、1.28m,直径1.25m的第2击夯沉量最大,比直径2.2m、2.5m、3m的单击夯沉量分别提高27%、75%、158%;经过第3击时,单击夯沉量分别为0.52m、0.59m、0.82m、0.95m,直径1.25m的第3击夯沉量最大,比直径2.2m、2.5m、3m的单击夯沉量分别提高13%、57%、78%;可以看出,前4次夯击中随着夯击次数的增加,直径1.8m夯锤的夯沉量相较于直径2.2m、2.5m、3m增加比例逐渐减少;缩小锤底面积可以增加夯锤动量,但随着夯击次数的增加,直径1.8m夯锤的夯沉量衰减速度更快;前4次夯击完成后,回填1/3~1/2夯坑深度的片石,回填片石后首击夯击的单击夯沉量分别为0.66m、0.89m、0.93m、0.92m。在随后的4次夯击中,可以明显看出,锤底面积越小,夯沉量衰减速度越快。
(3) 锤底面积变化时强夯置换的有效加固范围
图3-7为不同锤底面积下等效塑性应变云图,当夯锤直径1.8m、2.2m、2.5m和3m时等效塑性应变峰值分别为80%、79%、50%、43%,可以看出在夯击能不变的条件下,锤底面积越小,强夯置换完成后下部土体等效塑性应变越大,加固效果越好。当夯锤直径1.8m、2.2m、2.5m和3m时有效加固半径分别为3.2m、3.5m、4m、5m,随着锤底面积增大,强夯置换有效加固半径不断扩大;而有效加固深度分别为15m、13.6m、11.6m、10.2m,随着锤底面积增大,强夯置换有效加固深度深度不断减小。
因此在强夯置换施工方案设计中,可以有针对性地选择不同的夯锤底面积以达到不同的处理效果,大面积夯锤可以进行预处理达到设备进场目的,中等面积夯锤加固表土,较小面积夯锤加强置换挤淤深层加固效果。但也要避免锤底面积过小,首击夯沉量过大导致提锤困难,延误工期。
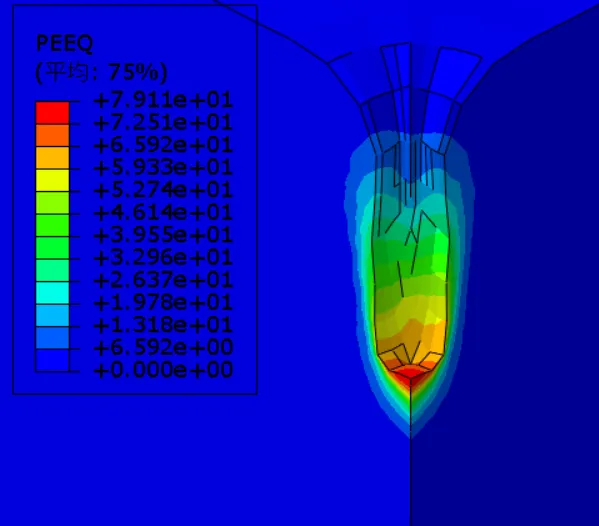
(a) 锤底半径1.8m
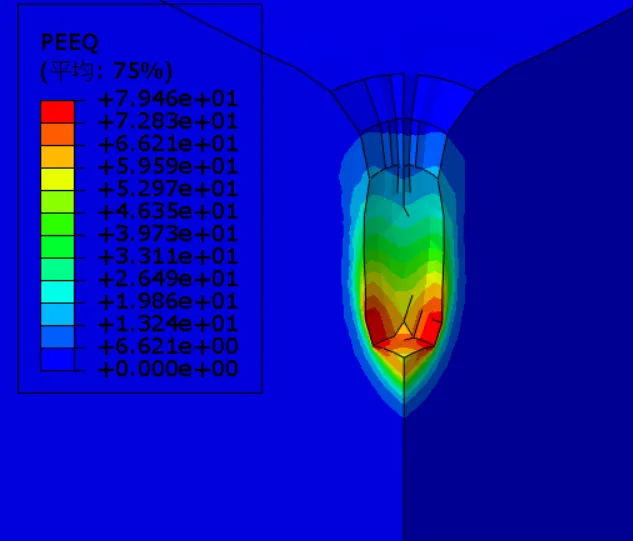
(b) 锤底半径2.2m

(c) 锤底半径2.5m
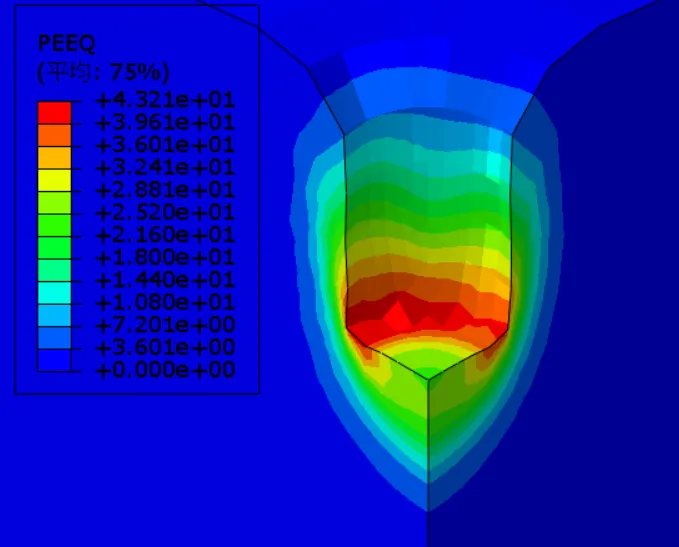
(d) 锤底半径3m
图3-7 不同锤底面积下等效塑性应变云图
图3-8为不同锤底面积下置换墩形状,曲线左上一侧为片石层,右下一侧为深软杂填土。可以看出,置换墩呈鼓状,墩体中部向两侧挤压变形。当夯锤直径1.8m、2.2m、2.5m和3m时,置换墩长度分别为7.66、7.18、5.5m、5.43m;而墩体直径分别为1.94m、2.26m、2.58m、3.2m,均大于其夯锤直径。随着夯锤直径不断减小,置换墩长度越来越长,但墩体直径也相应减小。另外,夯锤直径越小,动量越集中,能将片石夯入深层土体。因此,在设计施工中,考虑处理深度、置换率、现场土质情况,合理确定夯锤直径。
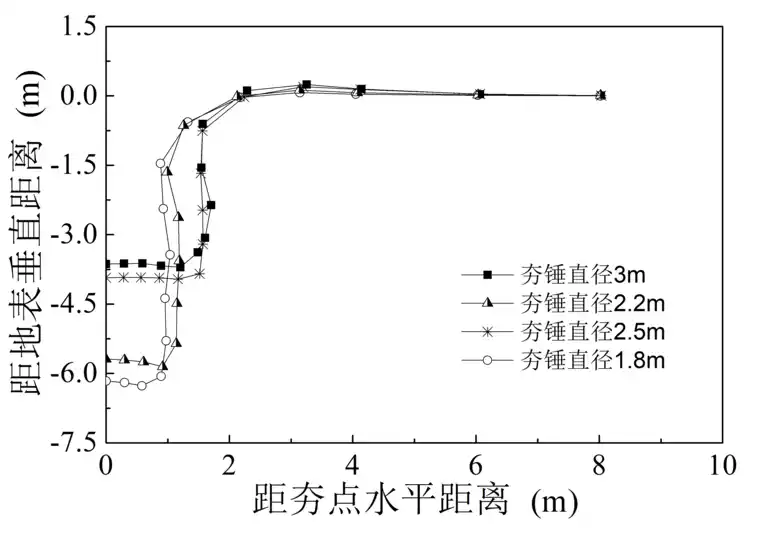
图3-8 不同锤底面积下置换墩形状

(4) 最佳夯锤直径
综上所述,随着夯锤直径不断减小,夯击完成后形成的有效加固直径也随之减小,有效加固深度不断增大。当夯锤直径为3m时, 有效加固半径最大约5m,设计时可增大夯点间距,节省工程造价;其有效加固深度最小约10.2m,不满足地基处理要求,而9次夯击后随着夯击次数增加有效加固深度增长幅度较小,增加夯击次数的经济效益极差;另外,。当夯锤直径为1.8m、2.2m时,有效加固深度分别为13.6m、15m,处理深度大,适合深层次加固;其有效加固半径分别为3.5m、3.2m,设计时必须加密夯点保证地基处理范围内土体均被有效加固,防止产生不均匀沉降,但夯点数量增多,工程造价增大;另外,单击夯沉量过大会产生吸锤现象提锤困难,耽误施工进度。因此,综合考虑地基处理深度和夯点布置,选择夯锤直径2.5m既满足高速公路地基处理深度要求又兼顾施工经济性。

3.3 同能级不同落距对加固效果的影响
强夯法处理地基施工简便,经济效益显著,得到广泛应用。但是如何控制强夯的加固效果,相同能级下是加大锤重还是加大落距,未有定量结论,另外锤重和落距的变化对施工机具和施工效率也有一定的要求和影响。一些学者对重锤低落距和轻锤高落距的强夯效果进行过比较研究,并普遍认为重锤低落距加固效果优于轻锤高落距。
吕秀杰、龚晓南等建议在湿陷性黄土中选用强夯法时,优先选用重锤低落距加固地基土;高广运等通过非线性有限元的分析,得出在同能级下,重锤低落距比轻锤高落距获得的夯后土体强度更高、夯沉量更大,有利于提高深层加固效果,李在卿通过从能量转化的角度分析和三个工程实例的比较,提出了在强夯单击夯击能相同的情况下,重锤低落距比轻锤高落距强夯效果好的结论;另外,徐万金通过比较重锤低落距与轻锤高落距强夯法对湿陷性黄土地基的加固效果,得出夯锤在接触土体瞬间的动量大小,是影响土体压缩变形的关键因素,动量大时加固效果显著。
前人的研究是针对常规(低能级)强夯时锤重和落距变化对强夯加固效果的影响进行研究,并且主要集中在定性方面。而对高能级强夯置换作用下,锤重和落距的选择对加固效果影响的定量研究尚未开展,本章通过对能级相同、锤重和落距不同对强夯置换加固效果及规律的进行分析,为高能级强夯置换的设计与施工提供参考依据,为进一步优化施工设计参数和提高效率、节约工程造价服务。
(1) 计算模型及参数的选取
计算模型采用1/4对称三维模型,计算范围径向取20×20m,深度方向取30m,网格尺寸0.33m×0.75m,共8800个网格;土体本构模型采用Mohr-Coulomb模型。
边界条件:模型竖向外侧固定水平位移;内侧竖向对称面采用轴对称边界;在土层底部,固定竖向和水平向的位移。
荷载的施加:夯锤底面直径2.5m,落距12.3m、18.3m、24.3m、30.3m、36.3m分别对应夯锤初速度15.8m/s、19.3m/s、22.2m/s、24.9m/s、27.2m/s;对应锤重65t、44t、34.2t、26.4t、22t。
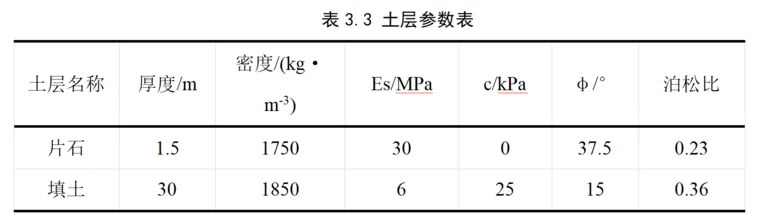
土层厚度30.0m,上层1.5m的片石土,各层土体计算参数如表3.3所示。
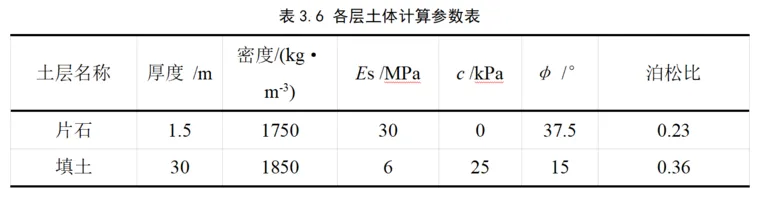
(2) 夯锤落距变化时的夯沉量
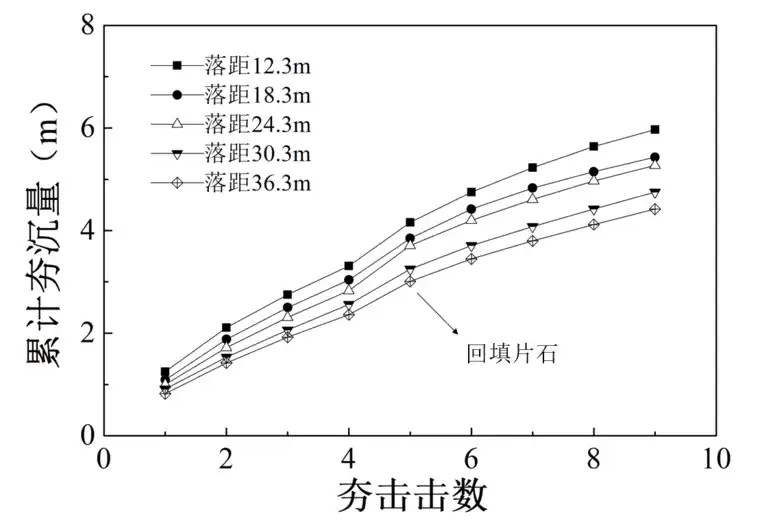
图3-9 夯锤落距变化时累计夯沉量与击数的关系
图3-9为夯锤落距变化时累计夯沉量与击数的关系。可以看出,不同落距的累计夯沉量均随着击数的增加而增加。经过全部9次夯击后累计夯沉量分别为5.97m、5.42m、5.28m、4.75、4.42m,落距12.3m的夯锤比落距18.3m、24.3m、30.3m、36.3m分别小了33%、49%、59%、66%,其最终沉降量分别大10%、13%、26%、35%。可以看出重锤低落相比于轻锤高落加固效果要好。
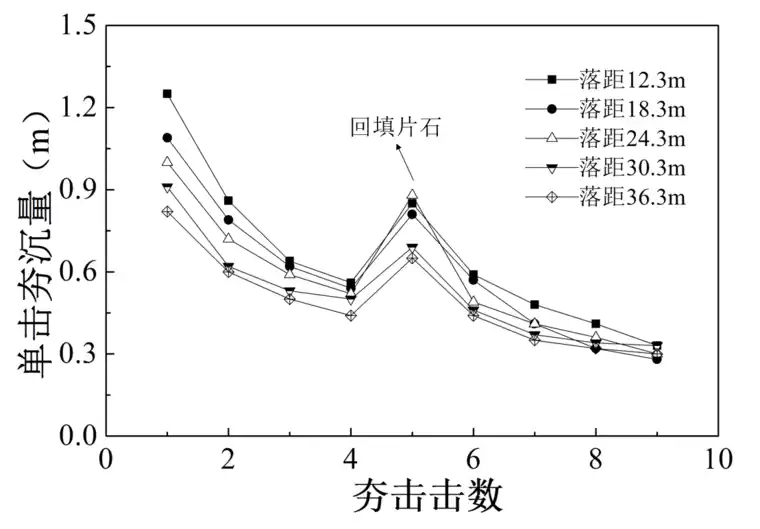
图3-10 夯锤落距变化时单击夯沉量
图3-10为夯锤落距变化时单击夯沉量关系。可以看出,前4次夯击随着击数的增加单击夯沉量越来越少,在回填片石后夯沉量显著增大,随后夯沉量不断减小。经过第1击时,夯沉量分别为1.25m、1.09m、1m、0.91m、0.82m,落距12.3m的首击夯沉量最大,比落距18.3m、24.3m、30.3m、36.3m的首击夯沉量分别提高15%、25%、37%、52%;经过第2击时,单击夯沉量分别为0.86m、0.79m、0.73m、0.62m、0.6m,落距12.3m的第2击夯沉量最大,比落距18.3m、24.3m、30.3m、36.3m单击夯沉量分别提高9%、18%、39%、43%;经过第3击时,单击夯沉量分别为0.56m、0.54m、0.52m、0.5m、0.44m,落距12.3m的第3击夯沉量最大,比落距18.3m、24.3m、30.3m、36.3m单击夯沉量分别提高4%、8%、12%、27%;可以看出,前4次夯击中随着夯击次数的增加,落距12.3m夯锤的夯沉量相较于落距18.3m、24.3m、30.3m、36.3m增加比例逐渐减少,在能级相同条件下增加锤重减小落距可以增加夯锤动量,提高强夯置换效果,但是随着夯击次数的增加,落距12.3的夯沉量衰减速度更快。回填片石后首次夯击的单击夯沉量分别为0.85m、0.81m、0.88m、0.69m、0.65m。在随后的4次夯击中,随着夯击击数的增加,夯沉量衰减速度加快。最终夯沉量趋于稳定。
(3) 夯锤落距变化时强夯置换的有效加固范围
图3-11为不同夯锤落距下等效塑性应变云图,当夯锤落距12.3m、18.3m、24.3m、30.3m和36.3m时等效塑性应变峰值分别为60%、52%、50%、45%、41%,可以看出,在夯击能不变的条件下,落距越小,强夯置换完成后下部土体等效塑性应变越大,加固效果越好。当夯锤夯锤落距12.3m、18.3m、24.3m、30.3m和36.3m时有效加固半径变化不大,均4m;而有效加固深度分别为15m、13.6m、11.6m、11.0m、10.6m,随着落距增大,强夯置换竖向有效加固深度不断减小。因此在强夯置换施工方案设计中,综合考虑经济、工期、处理深度等适当选用重锤低落可以提高强夯置换加固效果。
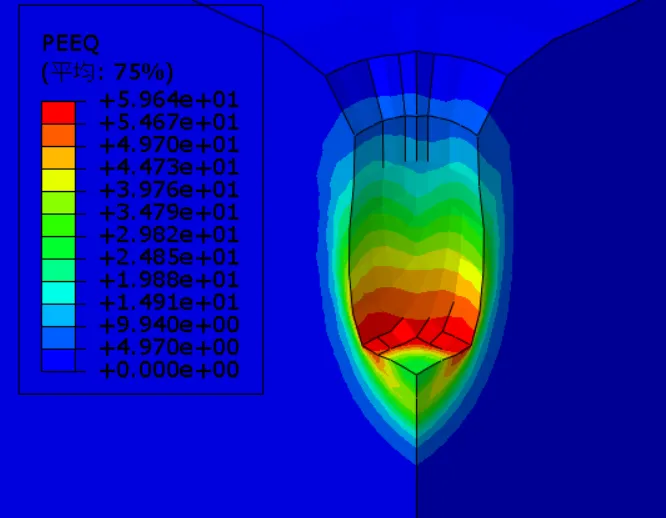
(a) 夯锤落距12.3m
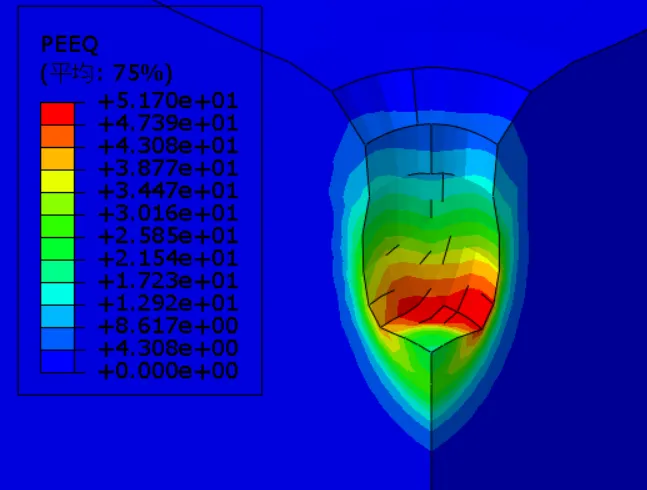
(b) 夯锤落距18.3m
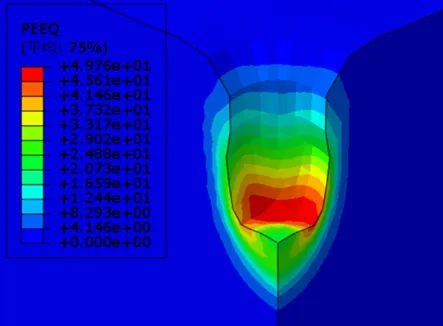
(c) 夯锤落距24.3m
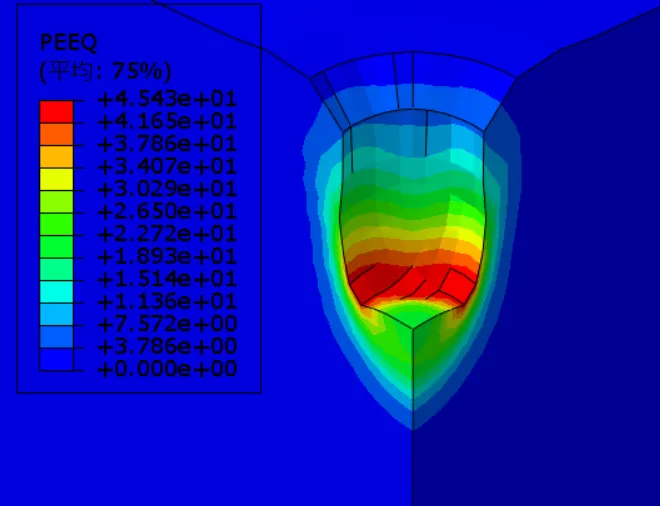
(d) 夯锤落距30.3m
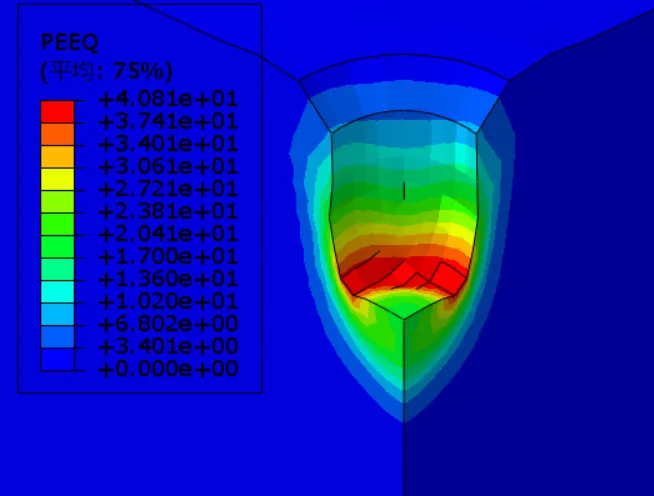
(e) 夯锤落距36.3m
图3-11为不同夯锤落距下等效塑性应变云图
图3-12为不同落距下置换墩形状,曲线左上一侧为片石层,右下一侧为深软杂填土。可以看出,置换墩呈鼓状,墩体中部向两侧挤压变形。当落距12.3m、18.3m、24.3m、30.3m和36.3m时,置换墩长度分别为7.5m、6.9m、5.5m、5.1m、4.8m,而墩体直径变化较小,约2.6m。随着落距的不断增大,墩体长度不断减小,因此在施工设计中采用重锤低落可以提高强夯置换加固效果,增大置换墩长度。
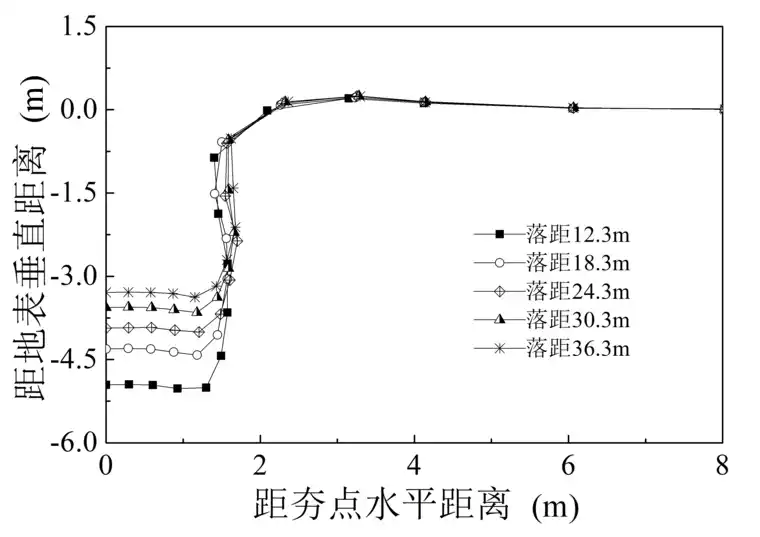
图3-12为不同夯锤落距下置换墩形状
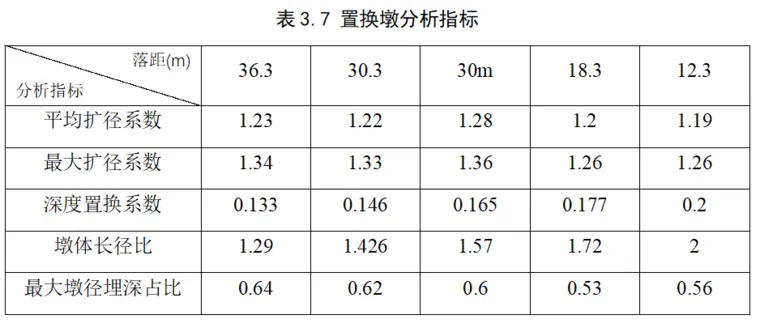
(4) 最佳夯锤落距
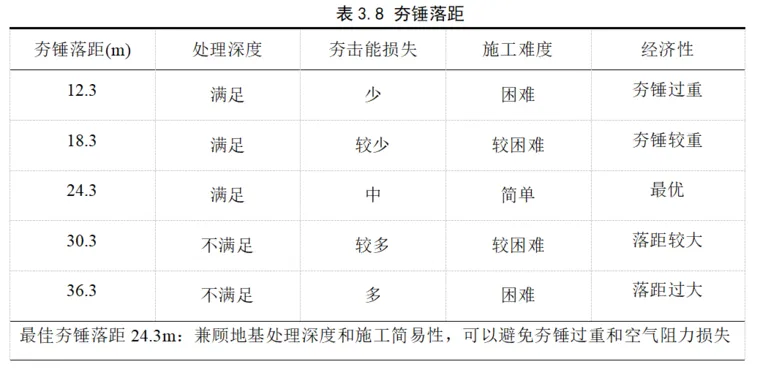
综上所述,随着落距减小,夯击完成后的有效加固深度不断增大。当落距36.3m、锤重22.9t时,有效加固深度约10.6m,不满足地基处理要求;实际工程中,在空气阻力作用下落距越高,夯击能利用率越小;另外,在侧风作用下轻锤易发生偏锤现象。当落距12.3m、锤重67.6t时,有效加固深度满足地基处理要求,也能有效减小空气阻力损失和侧风影响,但随着落距减小,锤重不断增大,夯锤制造和起吊困难。因此,综合考虑有效加固深度和施工简易性,选择24.3m为最佳夯锤落距。
3.4 不同高能级强夯的加固效果研究
随着工程建设项目的需要,强夯法的能级不断增加。现行2002年国家地基处理规范中强夯法最高能级仅为8000kN·m,亟待对更高能级强夯进行研究,进而指导高能级强夯地基处理的工程实践。强夯作用下土体的反应随地基土类型和输入能量的不同而不同。当能级大于6000kN·m时,随着强夯能量的提高,夯坑形状的发展及土体变形规律,强夯有效加固深度及有效加固深度如何变化,都是非常重要的问题,这关系到强夯能量是否得到有效利用,一味追求能级的提高是否有其现实意义。
本章计算分析能级分别为4000kN·m、6000kN·m、8000kN·m、10000kN·m、和12000kN·m的夯击作用下土体的变形和应力,研究能级的变化对强夯加固效果的影响。
(1)计算模型及参数的选取
计算模型的建立与第二章相同,计算中土层参数选取如表3.4所示。
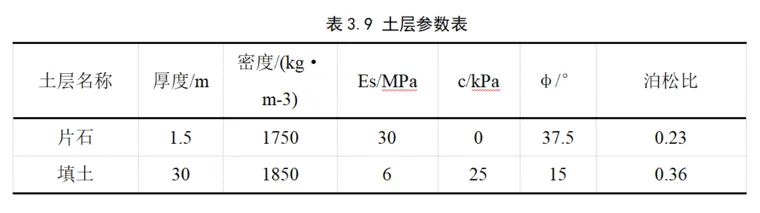
夯锤参数:落距24.3m,对于夯击能4000kN·m、6000kN·m、8000kN·m、10000kN·m、和12000kN·m,夯锤质量分别为16.4t、24.7t、34.2t、41.2t、49.4t。
荷载的施加:将夯锤置于地基表面,并施加22.2m/s的初速度冲击土体。
(2) 强夯置换能级变化时的夯沉量
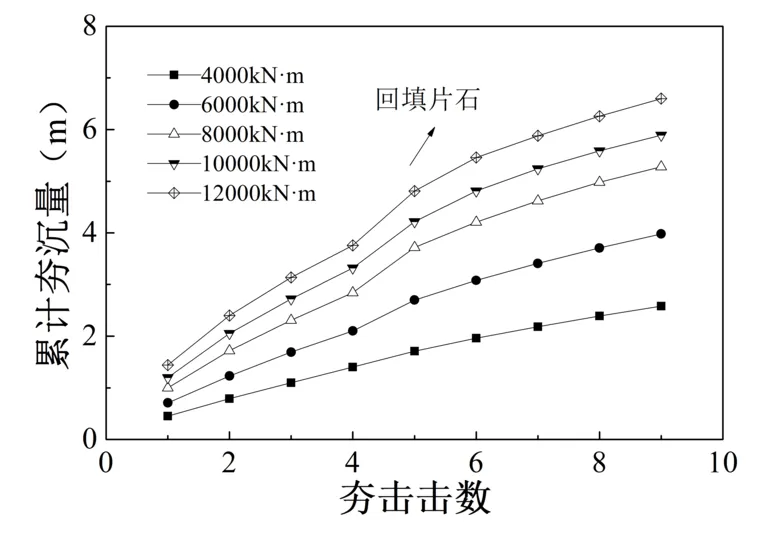
图3-13 夯击能变化时累计夯沉量与击数的关系
图3-13为夯击能变化时累计夯沉量与击数的关系。不同能级的累计夯沉量均随着击数的增加而增加。经过全部9次夯击后累计夯沉量分别为2.58m、3.98m、5.28m、5.89、6.6m,12000kN·m能级比4000kN·m、6000kN·m、8000kN·m、10000kN·m能级分别高200%、100%、50%、20%,最终沉降量分别大12%、25%、66%、156%。可以看出,随着夯击能的增大夯沉量不断增大,强夯置换加固效果越好。

图3-14 强夯能级变化时单击夯沉量
图3-14为强夯能级变化时单击夯沉量。可以看出,前4次夯击随着击数的增加单击夯沉量越来越少,在回填片石后夯沉量显著增大,随后夯沉量不断减小。经过第1击时,夯沉量分别为0.45m、0.71m、1m、1.2m、1.44m,12000kN·m能级的首击夯沉量最大,比4000kN·m、6000kN·m、8000kN·m、10000kN·m能级的首击夯沉量分别提高220%、103%、44%、20%;经过第2击,单击夯沉量分别为0.34m、0.52m、0.73m、0.85m、0.96m,12000kN·m的第2击夯沉量最大,比4000kN·m、6000kN·m、8000kN·m、10000kN·m能级单击夯沉量分别提高182%、85%、32%、13%;经过第3击,单击夯沉量分别为0.31m、0.46m、0.59m、0.67m、0.74m,12000kN·m的第3击夯沉量最大,比4000kN·m、6000kN·m、8000kN·m、10000kN·m能级单击夯沉量分别提高139%、61%、25%、10%;可以看出,前4次夯击中随着夯击次数的增加,12000kN·m夯锤的夯沉量相较于4000kN·m、6000kN·m、8000kN·m、10000kN·m能级增加比例逐渐减少,能级越高,夯沉量越大,但随着夯击次数的增加,12000kN·m的夯沉量衰减速度更快。回填片石后首次夯击,单击夯沉量分别为0.31m、0.6m、0.88m、0.9m、1.05m,在随后的4次夯击中,随着夯击击数的增加,夯沉量衰减速度加快,最终夯沉量趋于稳定。随着强夯能级的增大,相邻能级间的总夯沉量差值不断减小,因此在设计施工中,要针对地质条件合理确定最夯击能。
(3) 强夯置换能级变化时强夯置换的有效加固范围
图3-15为不同夯锤落距下等效塑性应变云图,当能级分别为4000kN·m、6000kN·m、8000kN·m、10000kN·m和12000kN·m时等效塑性应变峰值分别为60%、52%、50%、45%、41%,可以看出,夯击能越高,强夯置换完成后下部土体等效塑性应变越大,加固效果越好。夯击能不同时,有效加固半径变化不大,均4m;而有效加固深度分别为10m、11.6m、13m、14.4m、15m,随着能级增大,强夯置换竖向有效加固深度深度不断增大。因此在强夯置换施工方案设计中,综合考虑经济、处理深度、地质条件等适当选用高能级强夯可以提高强夯置换加固效果。
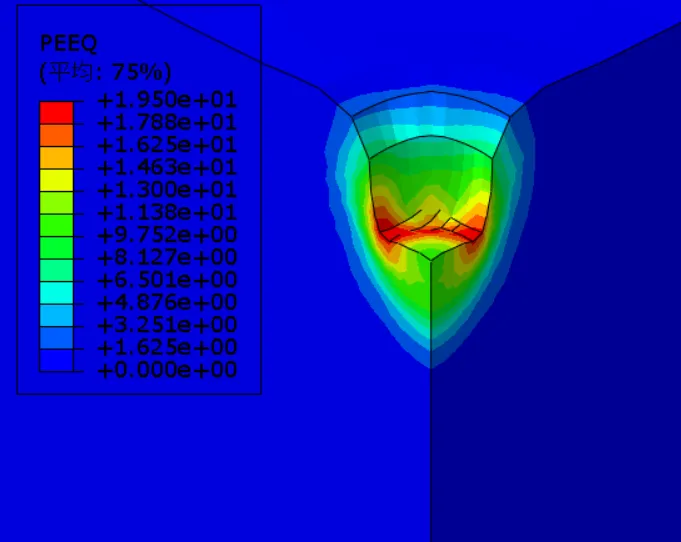
(a) 4000kN·m能级

(b) 6000kN·m能级
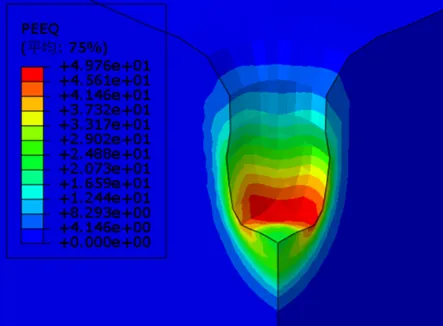
(c) 8000kN·m能级
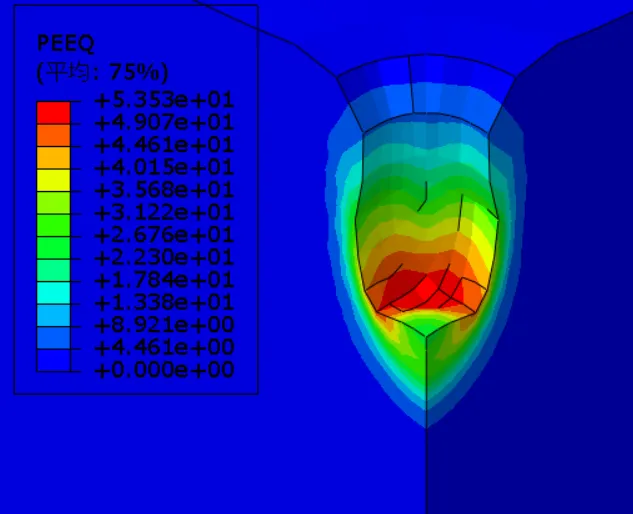
(d) 10000kN·m能级
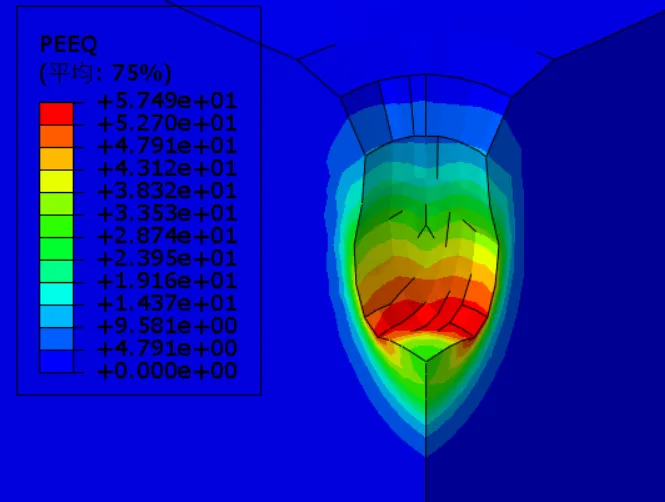
(e) 12000kN·m能级
图3-15 不同能级下等效塑性应变云图
图3-16为不同能级下置换墩形状,曲线左上一侧为片石层,右下一侧为深软杂填土。可以看出,置换墩呈鼓状,墩体中部向两侧挤压变形,当强夯能级4000kN·m、6000kN·m、8000kN·m、10000kN·m和12000kN·m时,侧向鼓起最大半径为0m、0.06m、0.16m、0.2m、0.24m,随着强夯能级的增大侧向鼓起半径不断增大,片石向两侧的挤压作用更为显著。当强夯能级4000kN·m、6000kN·m、8000kN·m、10000kN·m和12000kN·m时,置换墩长度分别为3.6m、4.6m、5.5m、5.8m、6.1m,随着能级增大强夯置换形成的墩体长度不断增大,但增长幅度越来越小,因此在强夯置换设计中必须通过试夯等确定最佳夯击能,保证施工的经济、高效。
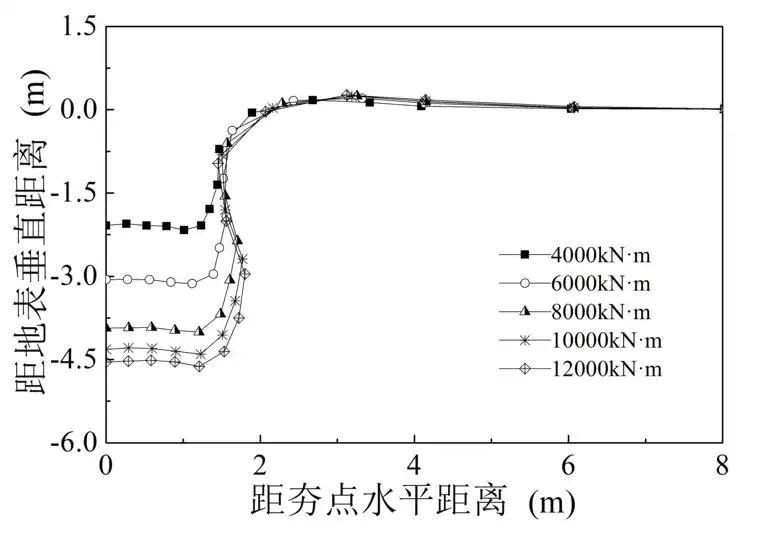
图3-16 不同能级下置换墩形状
4) 最佳夯击能
综上所述,随着夯击能增大,夯击完成后的有效加固深度不断增大,强夯置换作用更加显著。当夯击能4000kN·m、锤重16.5t时,有效加固深度约10m,不满足地基处理要求。当夯击能12000 kN·m、锤重49.4t时,有效加固深度约15m,满足地基处理要求,但根据图3-16夯击能10000、12000 kN·m置换墩长度增量较小,有效加固深度增量较小,片石侧向挤压作用显著,即片石在更高能级夯击作用下主要向两侧挤压变形,置换墩长度增加幅度不大,夯击能难以传递到更深层土体;另外,夯击能过高会产生超静孔隙水压力更大夯击能利用率下降。
3.5 小结
通过分析计算了不同深软杂填土厚度、夯锤底面积、落距、强夯能级下的夯沉量、土体变形和塑性应变,得出以下主要结论:
1)在8000kN·m能级强夯置换作用下能够有效加固深度12m、宽度4m的土体,并形成5.5m左右的置换墩。
2)随着夯锤底面积减小有效加固深度和置换墩体长度不断增大,而有效加固半径和置换墩半径不断减小。在实际工程中应考虑现场土质、处理深度、置换率等合理确定夯锤直径。
3)经过分析,重锤低落要优于轻锤高落。考虑到实际中空气阻力等,选择较低落距有利于提高强夯置换效果,节省造价。
4)随着强夯能级增大,片石的挤淤置换作用更加显著;有效加固深度和置换墩长度不断增大,但增长幅度不断减小;因此,根据设计施工要求合理选择夯击能级,充分利用夯击能。
耗时:4小时
处理器:i5-10210U CPU @ 1.60GHz 2.11 GHz
内存:8G
软件:Abaqus
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删