ABAQUS/Standard与非线性分析的高级对比

基础篇中我们介绍了线性，非线性问题，平衡迭代的过程，以及Static, general中的常规参数解释。高级篇中我们主要围绕着如下两点进行更深层次的讲解：

•收敛准则的调整

•时间增量的控制

首先需要明确的一点是，ABAQUS官方是不推荐修改这些高级的参数的，因为很多非线性问题的不收敛都是出于模型本身的问题。这些参数也都是ABAQUS官方经过很多工程实例调整的参数，既能保持求解的精度，也可以保证大部分问题的求解速度。

我个人认为即便我们不修改这些高级参数，对这些参数有一定的认识也是很不错的。至少能够理解为什么我们在做非线性问题的时候solver会报出这些和那些的错误。以及为什么会这样报错等。

如何找到这些参数？

Step module: other → General Solution Controls → Edit: 切换打开Specify

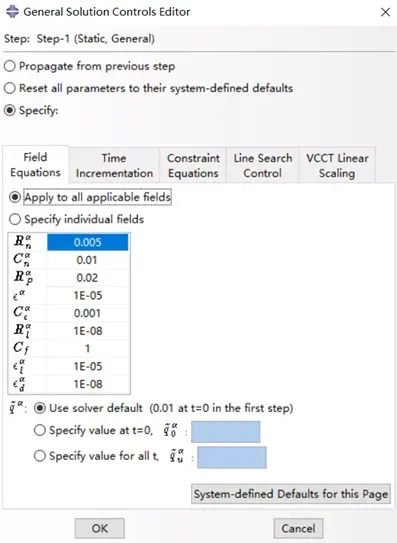
收敛准则相关术语：

R_n^α收敛准则是最大的迭代力残差对响应的平均流量q ̃^α的比值。默认值R_n^α=0.005，它对工程标准是相当严格的，但是在所有的情况下，除了特殊情况之外，将对复杂的非线性保证一个精确的解。如果为了计算速度可以牺牲一些精度的话，可以将此比值适当放大。

C_n^α 收敛准则是最大解校正对最大相应增量解的比。默认值为C_n^α = 0.01，与残差控制一起作为收敛准则中最重要的两个参数。对于某些分析如果不需要这样的精确性则允许增加此比值。

q ̃^α是ABAQUS/Standard为检查残差所使用的平均流量。默认的值是通过ABAQUS/Standard计算的时间平均流量，然而可以为平均流量定义一个不变的q ̃_u^α, 在此情况中，整个分析步上q ̃^α= q ̃_u^α。当使用指定容差时，为了便面测试解校正的大小，需要设置C_n^α =1.0

默认情况下t=0时， q ̃^α = 0.01， 也可以指定其他值，通过specify value at t=0.

非线性问题的收敛判断：

① 基本残差判断

即当r_max^α ≤ R_n^α * q ̃^α, 以及C_max^α ≤C_n^α * ∆u_max^α。两个条件都满足时，就接受当前解。

②零流量时

在某些情况中，有可能在一些增量过程中，具有零流量。即q ̅^α≤ ε^α* q ̃^α， ε^α=1E-05。以下两个条件满足任何一个都认为解是收敛的。

1. r_max^α ≤ ε^α * q ̃^α， ε^α=1E-05

 2. C_max^α ≤C_ε^α * ∆u_max^α， C_ε^α = 0.001

③线性增量

线性情况不要求每个增量都要一个以上的平衡迭代。在每一个场中通过最大残差与平均流量的严格比较时，可以考虑成线性的，并且不要求进一步迭代。如果在第一个之后的某些迭代步满足了此要求，则不需要对解的大小进行检查，可直接接受。

1.r_max^α ≤ R_l^α  * q ̃^α， R_l^α  = 1E-08

④非二次收敛情况下

在某些情况下，迭代的二次收敛是不可能的。因为牛顿法的雅可比是近似的。如果在Ip = 9次迭代后，收敛速度只是线性的，则ABAQUS/Standard使用一个较大的容差。 r_max^α ≤ R_P^α * q ̃^α， R_P^α  = 0.02，当然此时位移校正仍需要被满足

当有效的场是位移时，收敛准则要求最大的位移增量非常小时，那么∆u_max^α ≤ ε_d^α * f_β^α,  此时ε_d^α = 1E-08, f_β^α = 特征单元长度。

控制时间增量方案：

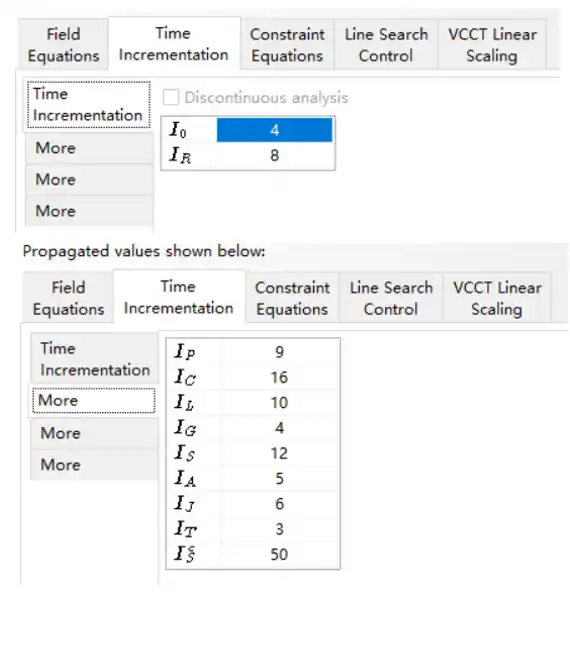
① General, I0和IR

可以使用求解控制参数来改变收敛控制算法和时间增量算法。其中I0和IR是非常重要的参数，I0是平衡迭代的编号，在此平衡迭代之后，会检查在俩次连续的迭代中残差是否增加, 默认I0=4。 IR也是平衡迭代的编号，在此平衡迭代之后开始对数收敛速率检查，默认IR=8。

在收敛困难时，选中Discontinuous analysis， I0和IR值将会增加，默认为I0=8， IR=10。 这样可以让在一个涉及摩擦和脆性材料模型的困难分析中，时间增量过早的消减。

② 因为单元或材料计算的问题，重新尝试一个增量

因为大位移问题中的极度扭曲，或者因为非常的塑性应变增量，ABAQUS/Standard可能具有单元计算的问题。如果发生了此问题，并选择自动时间增量控制，则将在不收敛后将时间增量乘以DH=0.25后，重新分析

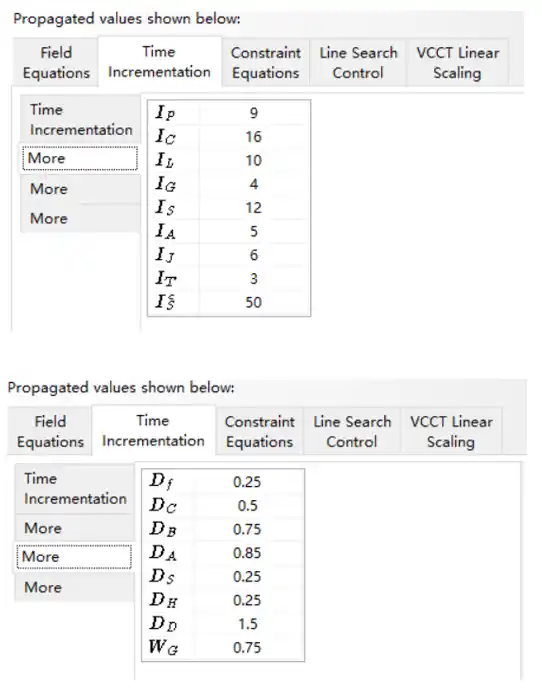
③ 再次尝试一个发散增量

有时候增量太大，使得求解根本不能收敛。根据上文之后，I0后将对残差r_max^α 的行为进行检查。如果解表现为发散时，那么就会停止当前增量步的尝试。而使用当前增量步时间乘以Df=0.25，同样也是缩短到之前的1/4来再次尝试求解。

④ 太多平衡迭代时，重新尝试一个增量

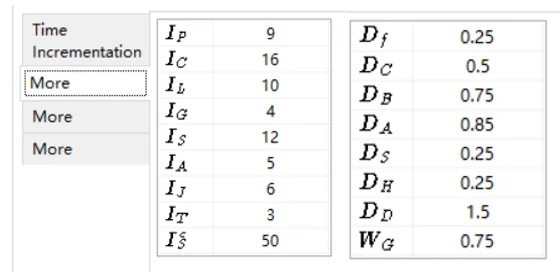
当迭代次数超过IR=8时，系统会探测收敛速率，如果发现收敛速率成减少趋势，那么在自动的时间增量下，则暗示最后不连续解之后的总迭代次数大于IC=16. 那么就会放弃此时的增量时间，乘以Dc后再次尝试求解，Dc=0.5。如果是固定时间增量，那么当迭代超过IC时，则分析终止伴随一个错误信息。

⑤ 为了效率，增加或者降低时间增量的大小

如果连续两个迭代不超过IG=4次迭代，则认为收敛是很轻松的，则可将时间增量放大DD倍。DD=1.5。如果一个增量收敛了，但是使用了多余IL=10个迭代步，那么下一个时间增量去当前时间增量的DB倍，DB=0.75。

⑥ 严重不连续迭代

当一个增量中，严重不连续迭代的次数超过Is=12时，那么就会放弃当前增量时间，乘以Ds = 0.25后再次尝试分析。

⑦ IA，连续缩减增量时间次数

IA是对增量步连续减少次数的控制参数，默认为5. 也就是说遇到难以收敛的问题时，增量步时间会一再降低，当次数到达5次后，系统就会终止计算并抛出错误。对于某些问题来说，5次是不够的，通常需要增加此值。

总结：

1、 ABAQUS官方并不推荐修改这些默认参数，当出现不收敛时首先检查自己的模型，当模型没有问题时，仍然不收敛。那么我们可能需要修改一下参数，来保证我们可以获得一个相对能够接受的解。

2、 增量时间控制，我们推荐使用Automatic Time Control，系统默认且可以求解速度最大化。

3、 我们在做分析时经常可以看到，增量步时间缩小到原来的1/4左右，学习了本篇之后可以看出，虽然都是缩小约1/4时间，但控制其缩小的参数并不相同。俗话说的好，对症下药，只要找到正确的原因，才能更好的对模型进行修正达到收敛的情况。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删