
问题描述:
这章主要介绍电子枪通电加热到 1050℃ 需要时间;断电整个过程电子枪各部件温度与时间的关系;阴极温度降为 200℃ 左右需要时间。
1. 电子枪仿真模型及前期设置
枪的简化模型:如图 1,模型主要包括控制极、控制极支撑件、外热屏、阴极支撑筒定位件、镍管、内热屏、阴极饼、钼筒、热丝及大枪壳等等。

图 1 枪有限元模型
网格设置:
有限元各部件网格大小及设置方法,模型划分网格后如图 2。

图 2 枪有限元模型
part 和接触设置:
我们先假设电子枪各部分是充分焊接的,所有体设置一个 part,不设置接触热阻。
辐射系数及设置:
电子枪中封闭的空间进行面面辐射设置,裸 露的部分进行面环境辐射设置,各种零件在不同分析模型中辐射系数相同,具体辐射对设置如图 3

图 3 各种辐射对辐射系数及辐射组
时间步设置:
瞬态时间步的总步数 (NumberOfSteps) 为 20 步,每步设置自动时间步,最小子步(MinimumSubsteps)为 1,最大子步(MaximumSubsteps)设置为 5,时间步设置参数及方法,如图 4。

图 4 瞬态时间步设置
温度载荷及环境温度:
电子枪工作的环境温度为 25℃ ,电子枪功耗以热生成方式加到热丝上,前 6400S 灯丝处于加电状态,之后灯丝断电,整个部件开始降温,如图 5。

图 5 不同时间点温度载荷
2. 仿真计算
仿真后,整个升降温过程中,阴极表面最高温度、阴极最高温度、内热屏最高温度、外热屏最高温度、控制极最高温度、阳极最高温度等随时间变化如图 6。

图 6 不同时间点各部件温度情况
加电6400S 时,阴极和枪上最高温度已经达到稳定,阴极表面最高温度达到1046.4℃,阴极最高温度为1101.3℃,
如图 7。

图 7 阴极温度分布
加电 6400S 时,内热屏筒上最高温度为 1047 ℃,最低温度 339.84 ℃,如图 8。

图 8 热屏筒温度分布
加电 6400S 时,外热屏筒上最高温度为 346.18 ℃,最低温度 277.85 ℃,如图 9。

图 9 外热屏筒温度分布
加电 6400S 时,控制极支撑件上最高温度为 246.44℃,最低温度 197.14℃,如图 10。

图 10 控制极支撑件温度分布
加电 6400S 时,控制极上最高温度为 246.68℃,最低温度 246.36℃,如图 11。

图 11 控制电极温度分布
加电 6400S 时,热屏支撑件的最高温度为 402.89 ℃,最低温度 256.1 ℃,如图 12。

图 12 阴极支撑筒温度分布
加电 6400S 时,阳极的最高温度为 179.51 ℃,最低温度 179.49 ℃,如图 13。

图 13 阳极温度分布
断电169 S,即 6569 S 时,阴极表面最高温度降为 200.51℃,阴极最高温度降为200.52℃,如图 14。
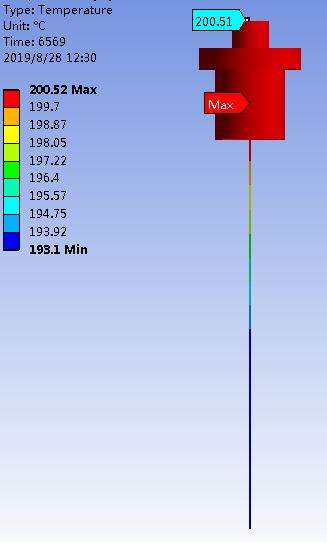
图 14 阴极温度分布
断电 169 S,即 6569 S时,内热屏筒上最高温度降为 200.5 ℃,最低温度 193.13 ℃,如图 15。

图 15 热屏筒温度分布
断电 169 S,即 6569 S时,外热屏筒上最高温度降为 198.84 ℃,最低温度 192.65 ℃,如图 16。

图 16 外热屏筒温度分布
断电 169 S,即 6569 S时,控制极支撑件上最高温度降为 194.27 ℃,最低温度 179.91 ℃,如图 17。

图 17 控制极支撑件温度分布
断电 169 S,即 6569 S时,控制极上最高温度降为 194.28℃,最低温度 194.23℃,如图 18。

图18控制电极温度分布
断电169S,即 6569S时,热屏支撑件的最高温度降为 193.53 ℃,最低温度 191.84 ℃,如图 19。

图 19 阴极支撑筒温度分布
断电169S,即 6569 S时,阳极的最高温度降为 173.62 ℃,最低温度 173.57 ℃,如图 20。

图 20 阳极温度分布
结论:
阴极温度降为 200℃ 后,随着时间的增加,阴极降温速度减慢,而且各部件温差会越来越小,实际计算时间和实际测量时间还会有一些差异,还需多次比对,进一步优化仿真。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删