Abaqus中运动耦合与分布耦合的区别与应用

本文讨论Abaqus中运动耦合约束和分布耦合约束之间的区别。这些约束类型之间的差异将在模型实例中加以展示。

介绍和用法

基于表面的耦合约束在Abaqus中主要用于以下目的：

• 将面上（从属）节点**的运动与参考节点的运动耦合。
• 当节点**要与参考节点定义的刚体运动耦合时，类型为运动耦合。
• 在平均意义上，当节点**耦合到由参考节点定义的刚体运动并且通过允许通过在耦合节点处指定的权重因子控制力的传输，此时类型为分布耦合。

耦合约束的几种典型应用：

• 向 模型施加载荷或边界条件。
• 为了在模型中分配载荷，可以用惯性矩表达式描述载荷分布。
• 在连续体和结构（梁或桁架）单元之 间的维 度 转换。
• 与其他约束（例如连接器单元）的交互进行建模。

耦合约束定义

Abaqus中的耦合约束是通过

interaction模块设置的。下面的图1显示了用于在Abaqus中建立耦合约束的各个窗口。
 

图1：Abaqus CAE中用于设置运动/分布耦合约束

对于耦合约束，需要指定的是参考节点（或约束控制点），耦合节点和约束类型。然后，耦合约束将参考节点与耦合节点相关联。

运动耦合约束

运动耦合将耦合节点的运动限制为参考节点的刚体运动。通过消除耦合节点的自由度来施加运动学约束。这意味着一旦用户在耦合节点上约束位移自由度的任何组合，便无法将其他位移约束，BCs，MPCs等进一步应用于该耦合节点。当旋转自由度已在耦合节点上受到约束（类似于位移）时，也会存在此限制。

运动耦合约束的主要建模窗口如下图2所示。

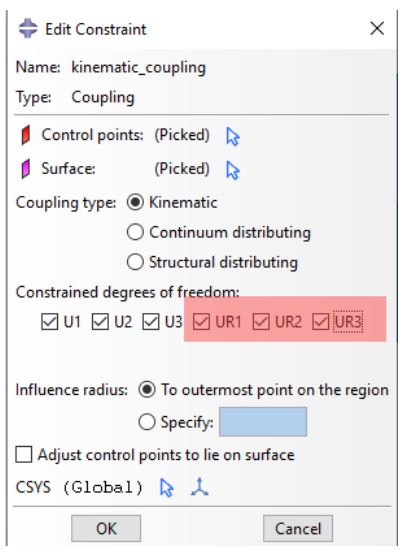
图2：运动耦合约束窗口和可用自由度

在运动耦合约束中，当所有3个平动自由度都受到约束时，耦合节点将跟随参考节点的刚体运动。

旋转自由度（UR）的不同约束组合将决定耦合节点中的旋转行为，这将与Abaqus中的现有MPC（多点约束）相同。

具体来说：

• 如果选择了所有三个旋转自由度（以及三个平移自由度），则运动耦合等效于MPC Beam。
• 如果选择了2个旋转自由度，则运动学耦合等效于Abaqus Standard中的MPC Revolute。
• 如果选择了1个旋转自由度，则运动耦合等效于Abaqus Standard中的MPC UNIVERSAL。

分布耦合约束

分布耦合将耦合节点的运动限制为参考节点的平移和旋转。与运动学上的不同，此约束在某种意义上是通过在平均意义上实施的，该方法可以通过在耦合节点处使用权重因子来控制从参考节点到耦合节点的传输负载。运动耦合约束的主要建模窗口如下图3所示。

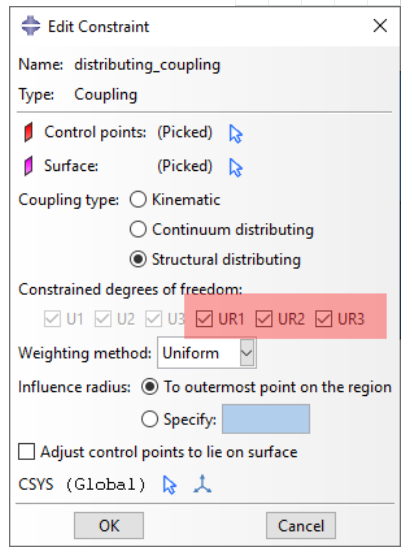
图3：分布耦合约束窗口和可用自由度

在三维分析中，用户可以通过仅指定约束中的平移自由度，释放所有三个力矩约束（UR1-UR3）。

在这种情况下，参考节点中只有平移自由度有效。

在这种情况下，对约束节点的行为的影响将在本文稍后显示的Abaqus示例中进行演示。

示例

图4中显示了网格模型的几何形状。它是一个用3d实体单元（C3D8I）建模的梁。它的横截面是矩形（250x250毫米），长度等于2m。

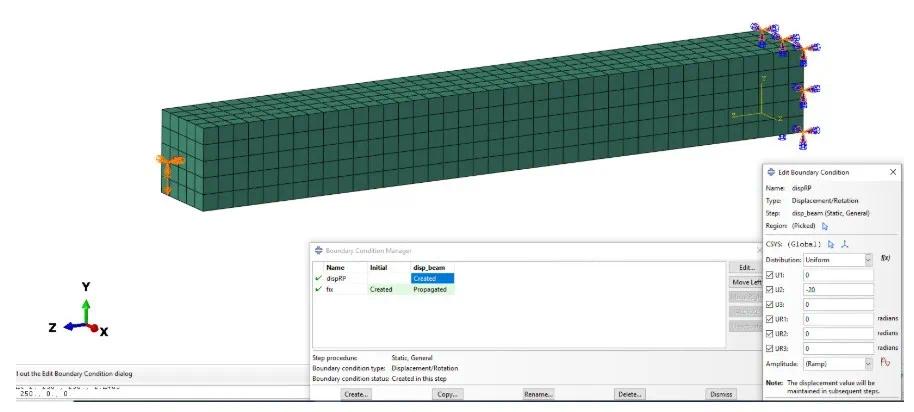
图4：示例的网格模型

荷载和边界

梁右端完全固定，而垂直位移（-Y）施加在距离梁左端50 mm的远端（RP）上。将适当的边界条件施加到远程点（也是耦合的参考节点）上，以约束横向（X）和轴向（Z）位移。如图5所示。

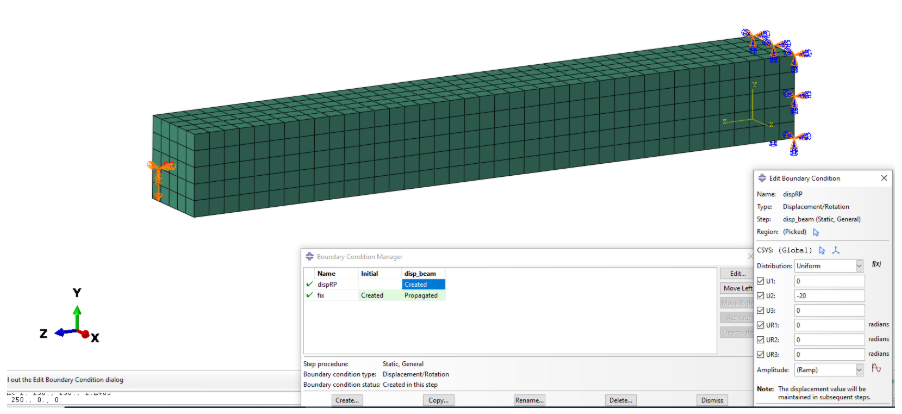
图5：载荷和边界条件

为了进行结果比较，使用运动耦合和分布耦合，将远端耦合到梁的左端面。

在图6中显示了具有运动耦合约束的设置。

在图6的红色框中，还显示了用于实现分布耦合约束的设置修改。所有耦合节点的自由度都受约束于参考节点的自由度。

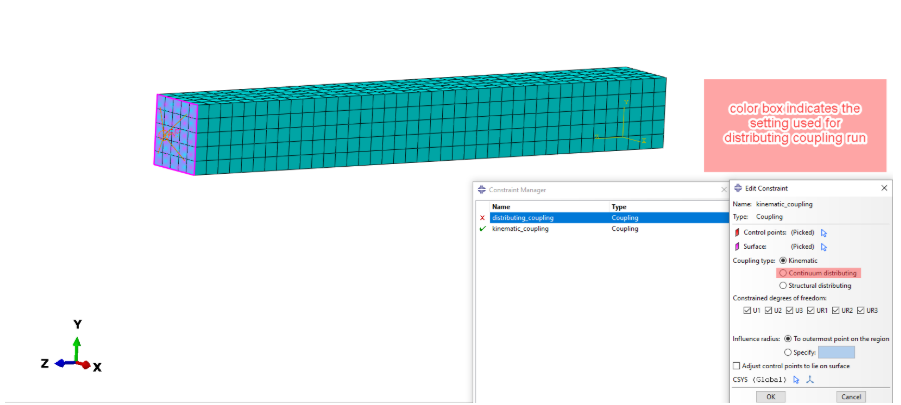
图6：耦合约束定义

材料

使用普通钢材进行线性弹性仿真。

结果比较1

在垂直位移（20mm）下加载的梁的变形形状在图7中显示（放大了20倍）。在梁的右端，它与未变形的形状（灰色）重叠。左端则产生了明显的变形，但是两个耦合约束之间偏转的形状相差不大（运动与分布）。

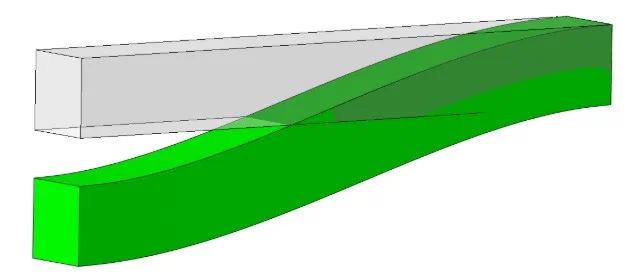
图7：示例梁的变形与未变形形状

仔细观察轴向位移（Z）的等高线图，可以发现两个耦合约束之间的差异。

图8中给出了此细节，其中显示了U3位移。相应地调整了极值显示的设定，以增强在包含耦合节点的梁的左端面的结果显示。上部轮廓��来自运动耦合，下部轮廓来自分布耦合。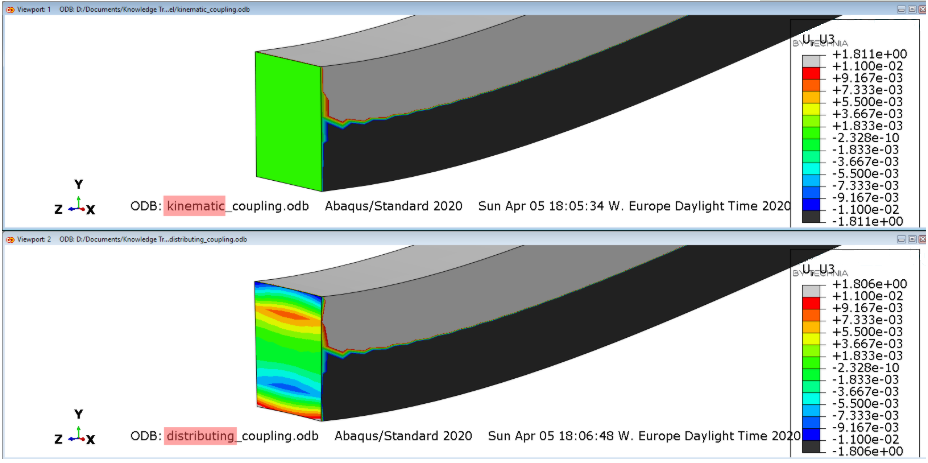

图8：U3位移比较（以毫米为单位）

对于运动耦合约束（上图），所有耦合节点的自由度都耦合到参考节点的刚体运动节点。因此，这些节点的U3位移严格为零，遵守了应用于参考节点的边界条件。本质上，在运动学耦合中，消除了耦合节点上所有受约束的自由度。

另一方面，分布约束（下图）允许耦合节点的相对变形，如在图上看到的（U3位移不为零的红色和蓝**域）。

结果比较2

作为补充延伸，对两种耦合类型的约束自由度进行了修改，并重新进行了分析。这样做是为了研究运动耦合和分布耦合之间在约束执行方面的差异，并且还可以了解如何施加分布耦合。

修改后，只有平移自由度（U1，U2，U3）在耦合定义中耦合。模型输入的其余部分保持不变。

变形形状的侧视图如图9所示。

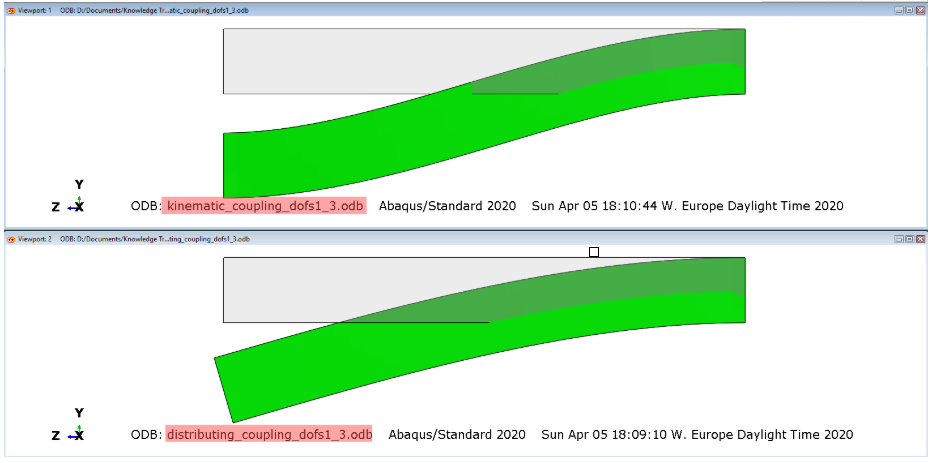
图9：在耦合定义中释放了UR的变形形状

从下图可以看出，使用分布耦合时，梁的末端可以旋转。

发生这种情况的原因是，只有在耦合节点的至少一个旋转自由度被耦合时，参考节点上的旋转自由度才被激活。

如果不是（这里就是这种情况），则参考节点的UR保持不活动状态，从而允许梁的末端旋转。

总结

• 当必须抑制结构的特定运动模式时，运动耦合是有用的。一个应用例如可以是薄壳状结构的纯弯曲，其中横截面必须呈椭圆形但保持平面。
• 分布耦合允许对从RP到耦合节点的负载分布进行更多控制。可以使用其他选项（而不是“完全一致”）。运动耦合则不能。
• 连续耦合是一种特殊类型的连接，即仅允许在耦合节点力（而不是力矩）的传递。这可以有特殊的应用。
• 分布耦合必须始终限制耦合节点上所有可用的平移自由度。运动耦合不是这种情况。
• 一旦在运动耦合的耦合节点中耦合了至少一个（或组合）自由度，就将消除所有自由度。分布耦合不是这种情况。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删