Abaqus中的运动分散耦合技术

结构耦合和运动耦合都具有将选定表面上的节点集合（耦合节点）的运动耦合到参考节点的运动的共同目的。

本节概述了两种方法之间的一些差异。

1约束执行的性质

•运动耦合以严格的主从方法执行。消除了耦合节点处的自由度（DOF），并且将约束耦合节点随参考节点的刚体运动而移动。

•从平均意义上讲，必须进行分布耦合。没有消除耦合节点处的自由度。相反，约束是通过分配负载来强制执行的，例如：

–耦合节点处的力合力等于参考节点处的力和力矩，并且维持参考点周围分布载荷的力和力矩平衡。

运动耦合约束不允许受约束的自由度之间发生相对运动。但是，它确实允许无约束的自由度之间的相对运动。

分布耦合允许受约束和不受约束的自由度之间的相对运动。耦合节点的相对运动将使分布负载的平衡条件得以维持。

例如，考虑图4.2所示的悬臂梁。它与二阶砖元素网格化，并内置在右端。在自由端定义了耦合约束。端面节点的自由度1到6

包含在约束中。在参考节点上，沿垂直方向施加位移，而所有其他位移和旋转分量保持为零。

使用运动学和分布约束方法分析模型；两种约束类型的梁的变形形状相似，如图4.3所示。仔细检查梁耦合端的位移，可以发现两种约束方法的结果之间存在差异。图4.4和4.5分别显示了分布和运动学方法在梁自由端的轴向（3方向）位移的轮廓。

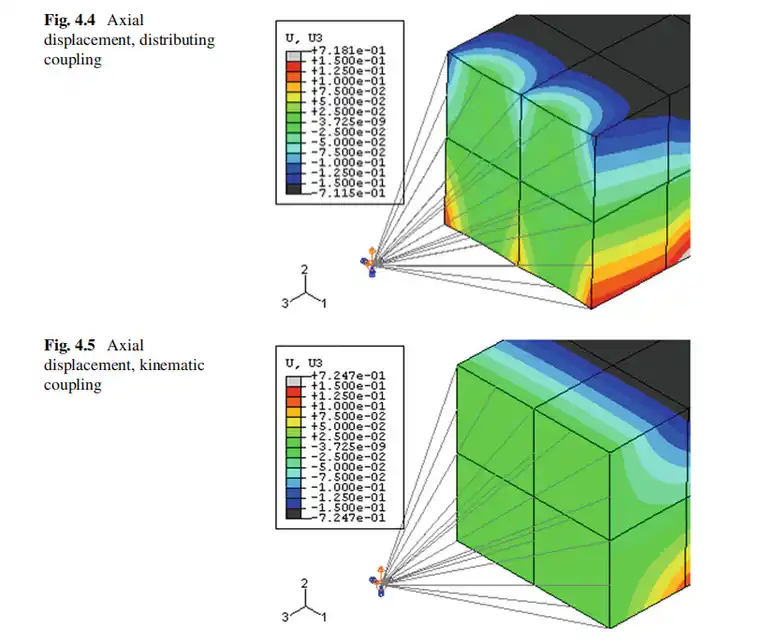
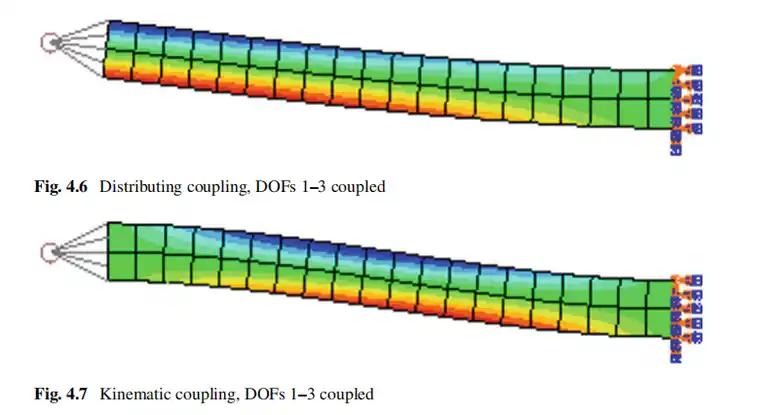
如图4.4所示，分布耦合允许梁末端的节点经历相对变形，而如图4.5所示，由于它将耦合节点的运动约束到参考节点的刚体运动，因此运动耦合，不是。轴向（以及横向）方向的位移相同为零由于参考节点上的边界条件。继续上面的示例，请考虑仅耦合自由度1-3的情况：轴向位移的轮廓如图2和3所示。分布方法和运动学方法分别为4.6和4.7。

图4.6显示，通过分布耦合，梁的末端可以自由旋转。图4.7显示了受束端旋转限制的运动学耦合。这是因为仅当至少一个从动旋转自由度被耦合时，分布耦合的参考节点处的旋转自由度才起作用。相反，所有自由度在参考节点上均处于活动状态

运动耦合约束的大小，独立于参与约束的从动自由度。必须在参考节点的无约束DOF上放置适当的约束，以避免数值奇异。当必须抑制结构中的特定运动模式时，运动耦合约束是有益的。一种应用是模拟薄壁管道中的纯弯曲，在该管道中，横截面必须呈椭圆形，但保持平面。附录A.1概述了此示例的详细信息。分布耦合允许对从参考节点到耦合节点的负载分布进行更多控制。除了均匀分布外，还可以使分布相对于参考节点的距离线性，二次或三次减小。运动学方法未提供任何控件。分布耦合必须始终限制耦合节点上所有可用的平移自由度。对于运动耦合约束，这不是必需的。

一旦在运动学耦合约束中指定了耦合节点处的自由度的任何组合，则其余自由度均不可用于进一步约束。分布耦合不是这种情况。

附录A.2。中提供了其他详细信息。对于两种约束类型，都可以应用集中载荷或位移

在参考节点上。分布式耦合定义中的大量耦合节点可能会导致过多的内存使用和较长的运行时间。这是形成约束时产生的大波前的结果。

2在Abaqus / CAE中定义约束

在Abaqus / CAE的“交互”模块中定义了耦合约束。 首先定义要耦合的表面。 然后，如果参考节点不是现有节点的一部分几何，必须使用“工具”→“参考点”创建一个单独的参考节点。然后选择：约束→创建...→耦合→选择参考节点→选择耦合面。将出现“编辑约束”对话框，从中可以选择约束类型和耦合的自由度。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删