Abaqus/Explicit动态流固耦合分析技术

首先，我们假设对手打过来一个高抛球，到我们这边与球拍撞击时，羽毛球与垂直方向夹角30°，球速10m/s，球拍沿水平方向迅速打击，给羽毛球一个瞬时冲量，这里的拍网采用带预紧拉伸的truss单元来模拟。

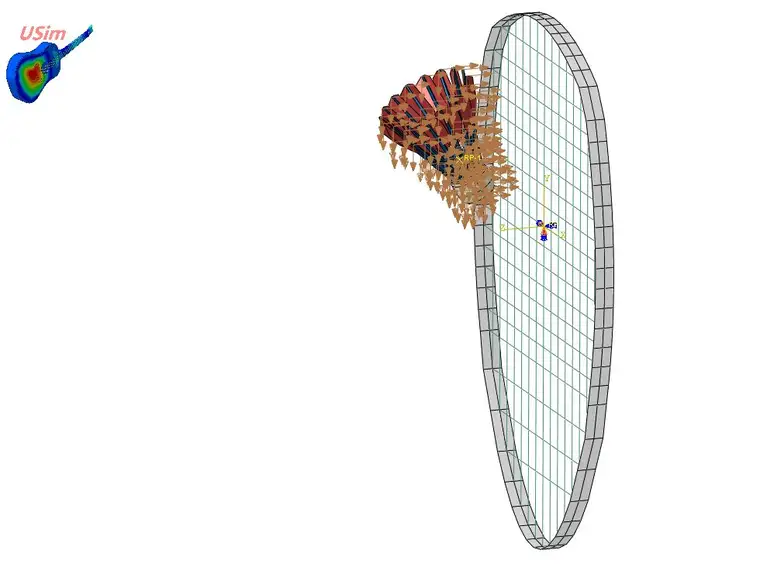
边界条件设置

通过Abaqus/Explicit仿真计算得到羽毛球在拍子击打的瞬间，它的动态变形与运动状态如下图所示。

羽毛球受到球拍打击的瞬间

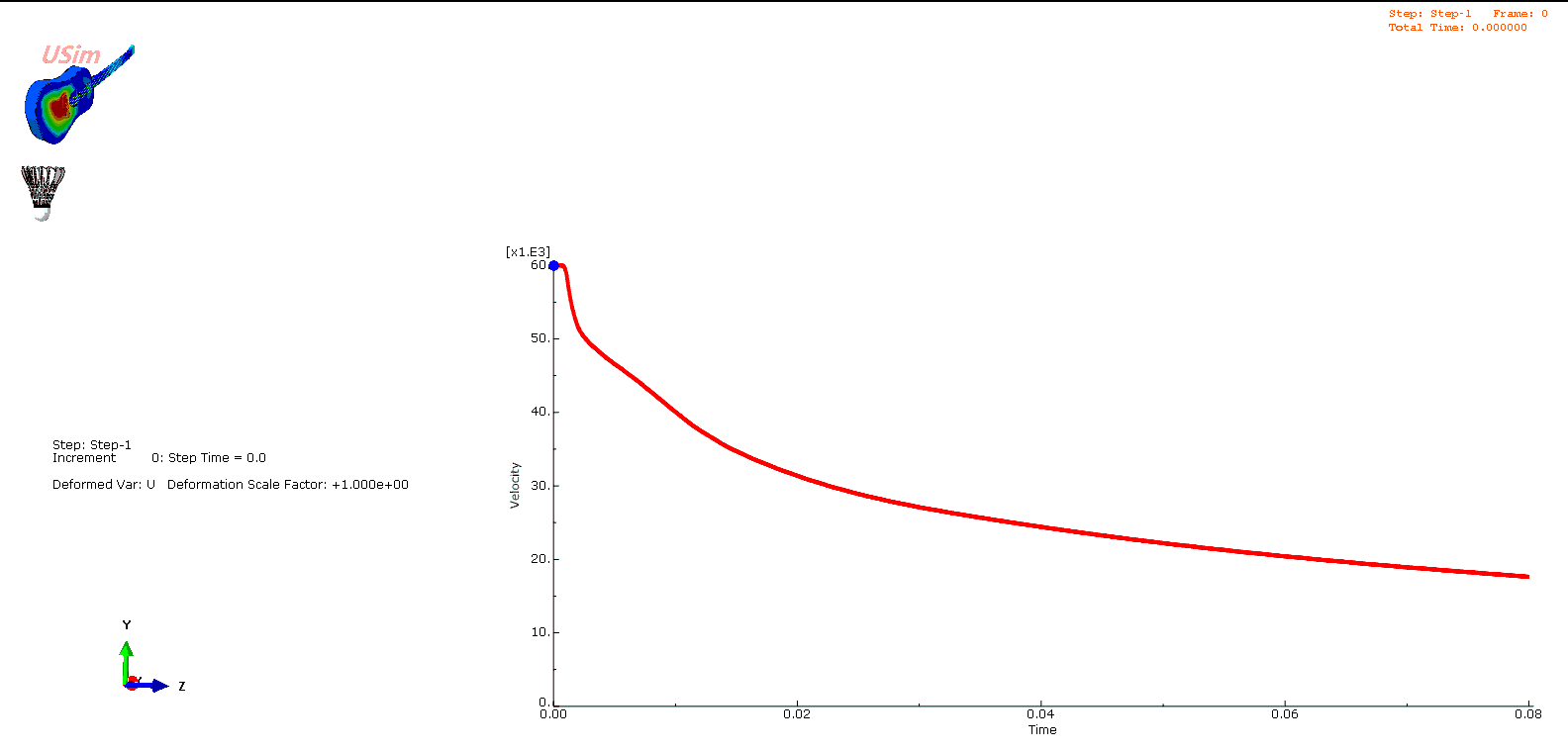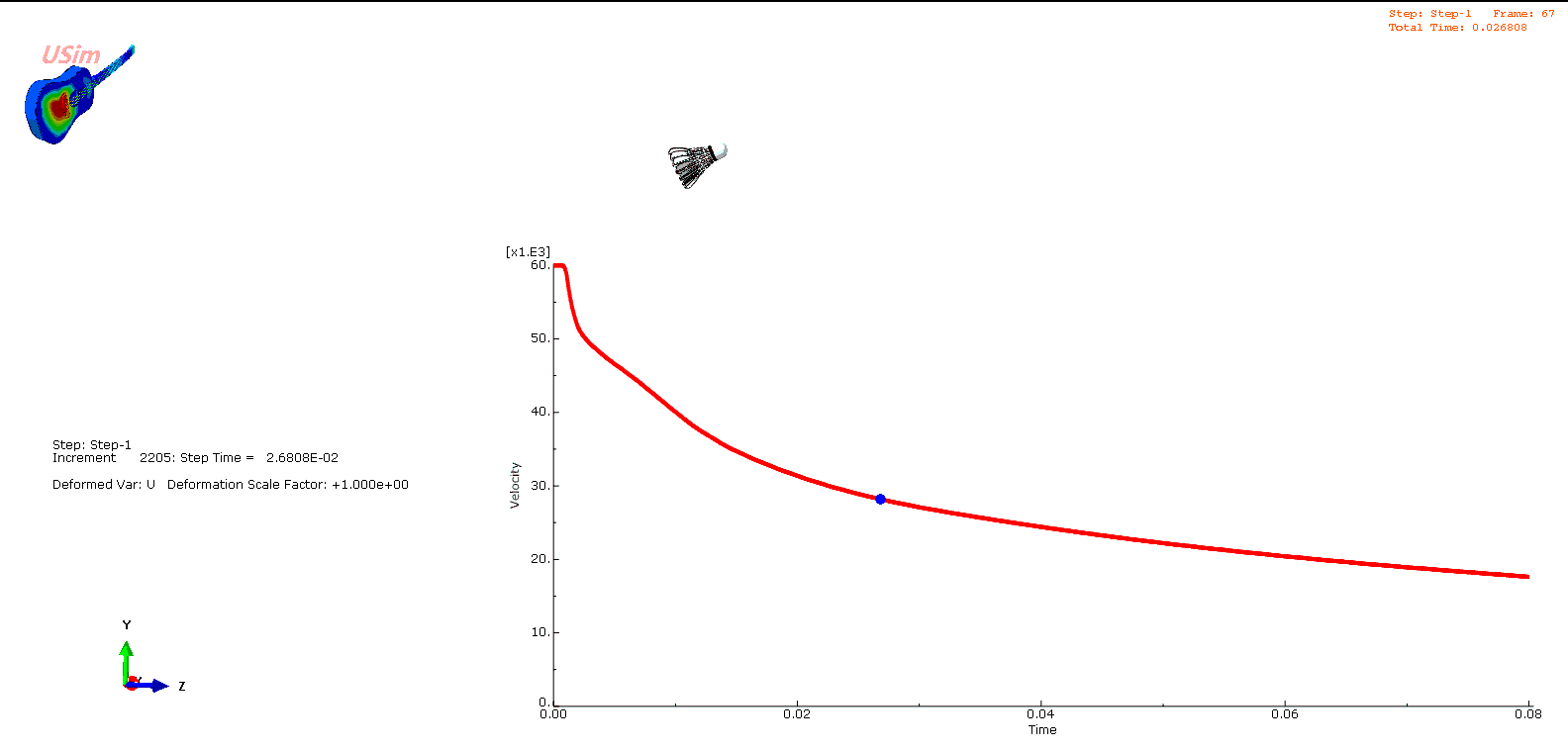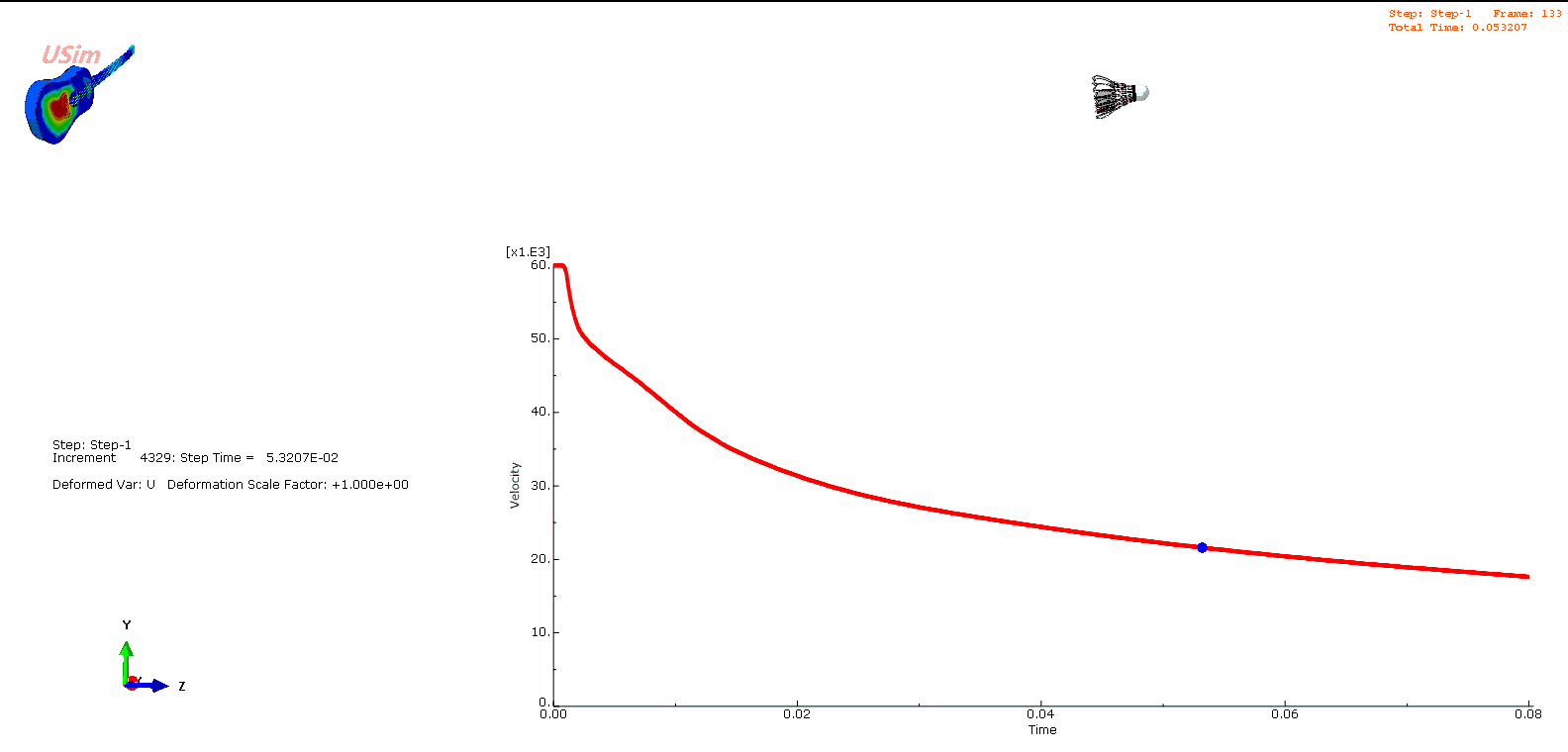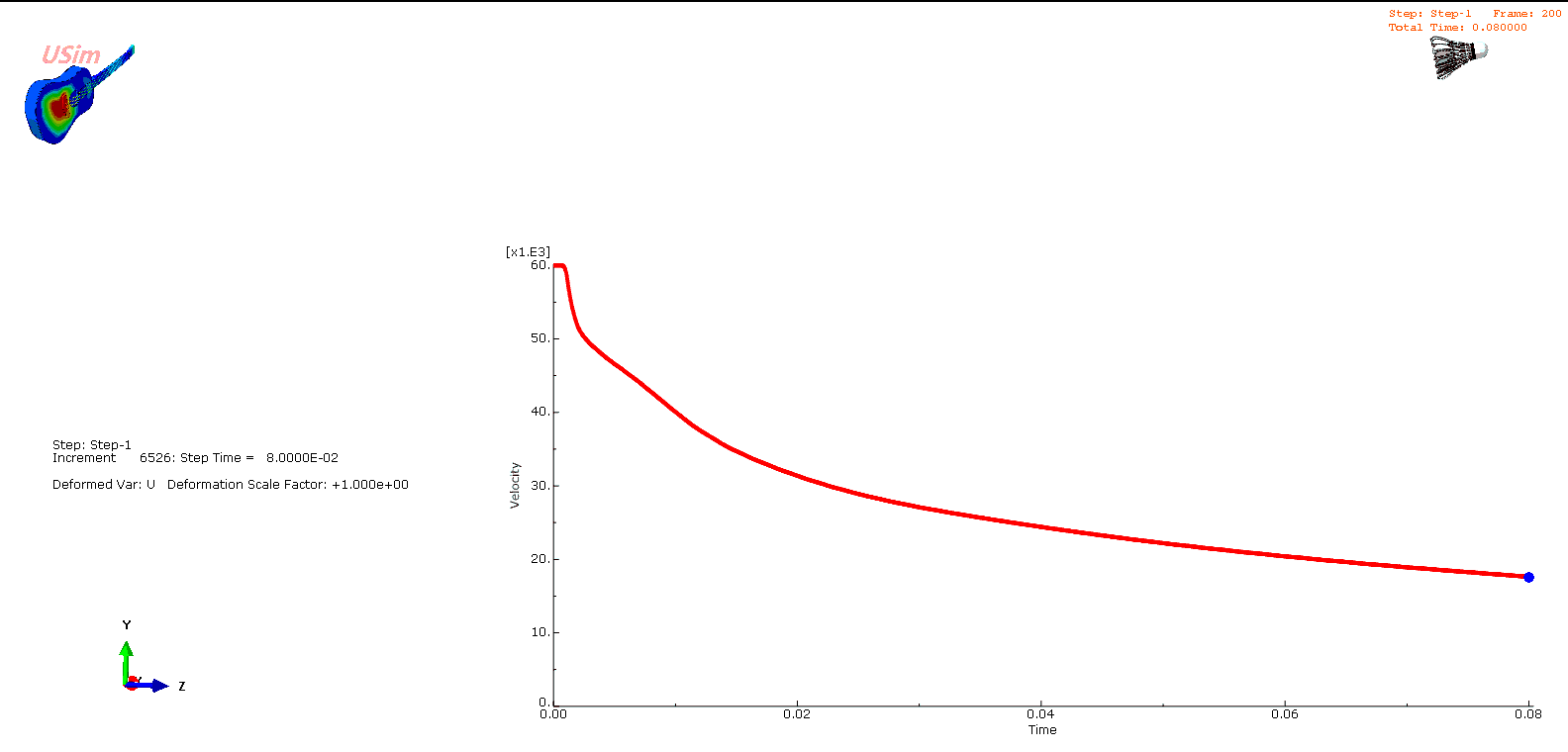
我们还可以获得羽毛球的速度曲线与其离拍之后的运动姿态，可以看到羽毛球在离拍的瞬间获得60m/s的初始速度。

羽毛球上某测点速度曲线

你应该已经注意到了，上面的仿真结果中，羽毛球并没有调头啊？是的，我们忽略了一个极其重要的因素：空气阻力。

由于打击过程考虑了羽毛球的变形，再考虑流固耦合的话，计算耗时巨大，我们就单纯的分析羽毛球姿态变化而言，合理地简化一下这个过程：

a. 假设羽毛球从接触到离开网拍的过程中（1ms左右），空气对羽毛球的离拍速度影响可以忽略不计；

b. 假设离拍后空气和羽毛球的相互作用过程中，空气阻力致使羽毛球的变形是极小的，并且对于姿态分析是无关紧要的。

抛去这些次要因素，再通过流固耦合方法来分析羽毛球的姿态变化就简单多了，在这个分析过程里，羽毛球考虑为刚体，刚体上的拉格朗日网格与空气域的欧拉网格进行相互接触。我们以前面的仿真为基础，取离拍的瞬间，球头竖直向下、初始速度60m/s，方向水平作为流固耦合分析时羽毛球的初始状态。

注意，为了节省计算时间，这里仅对羽毛球可能划过的区域进行空气域建模，欧拉边界离相互作用区域比较近，针对这个问题而言，要对所有面设置无反射边界条件。

羽毛球姿态变化的CEL分析

通过Abaqus/Explicit计算可以得到羽毛球的姿态在空气阻力作用下，调整为指向球头的状态。

羽毛球在空气中的运动

并且，羽毛球的速度在80ms内降到了20m/s，这个过程中它向前运动了2.3m左右，这样看起来就比较正常了，在后面的运动过程中，它还会持续受到空气阻力的作用，继续减速，最终获得稳定的下落速度（理想空间内，不受其他阻碍的状态下）。

羽毛球划过的流场（剖面）

Abaqus算得羽毛球的姿态变化过程

这个调头动作得益于羽毛球的形状与质量分布特点，也即是其压心与质心的位置关系能够很好地满足静稳定飞行要求。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删