FLUENT管路自然循环流动模拟案例

1 前言

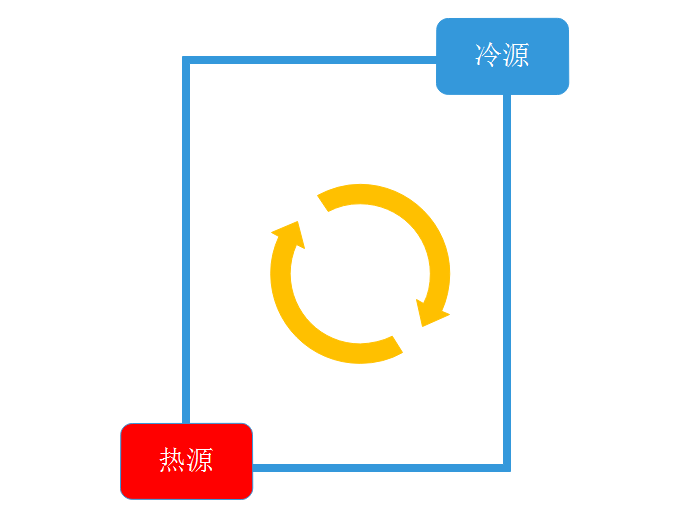
所谓自然循环，指的是在封闭的管路系统中，不借助外部驱动力，仅靠冷热流体的密度差和冷热源位置的高度差形成的浮升力驱动流体流动的一种能量传输形式。在先进核电系统中，非能动余热排出系统的设计理念本质上就是自然循环机制的利用。通常，自然循环回路的热源处于较低的位置，冷源处于较高的位置（如下图）[1]。这种案例的数值计算最大的挑战在于计算量大，首先因为整个回路的管道通常很长，多数情况无法简化成二维计算，离散化网格数量巨大；其次，这种问题属于封闭空间的自然对流问题，基本上很难通过稳态计算达到收敛解，需要通过瞬态计算来解决，这又增加了计算量。今天，我们用一个相对简单的自然循环回路来做一个计算案例。
 

2 建模与网格

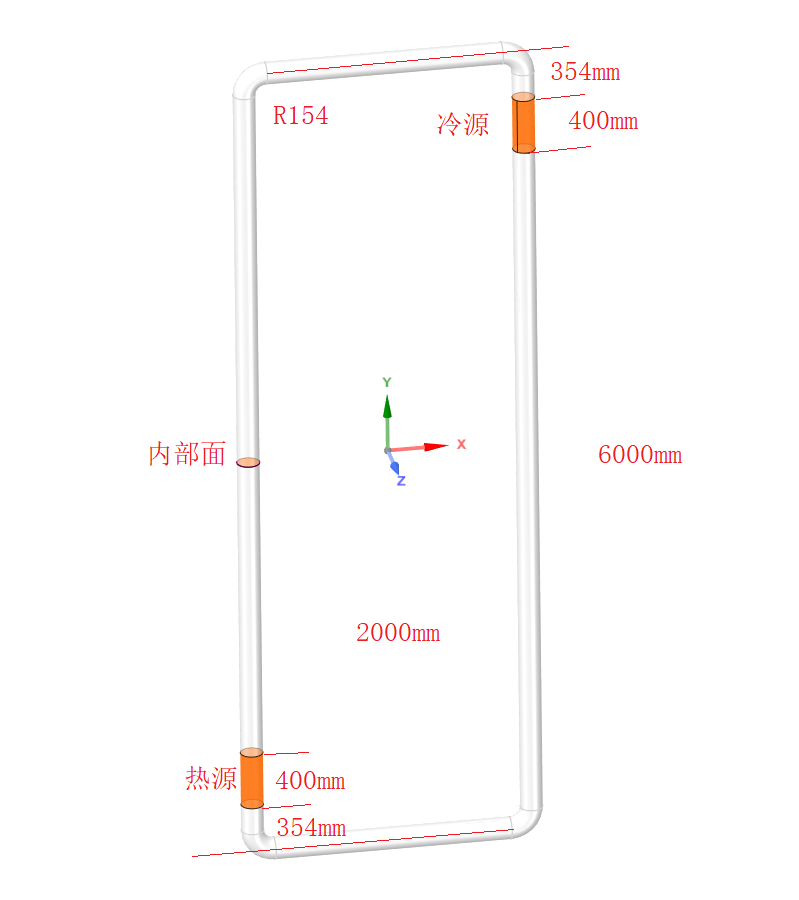
建立如下的矩形回路，回路高6000mm，宽2000mm，管道直径φ160mm，介质为常压液态水，四个边角的弯曲半径为R154mm。回路左下方和右上方分别是热源和冷源，长度均为400mm，热源底部距离回路底部管道轴线354mm，冷源顶部距离回路顶部管道轴线354mm。热源为98℃恒温面，冷源为30℃恒温面。划分多面体网格，节点数约45.4万，最小正交质量约0.5。建模时，为了后续计算监测回路的自然循环流量，在管道截面上建了一个内部面。
 

3 求解设置

开启重力项。
 

采用realizable k-e湍流模型，近壁处理采用加强壁面函数，该方法通常要求Y+＜5。
 

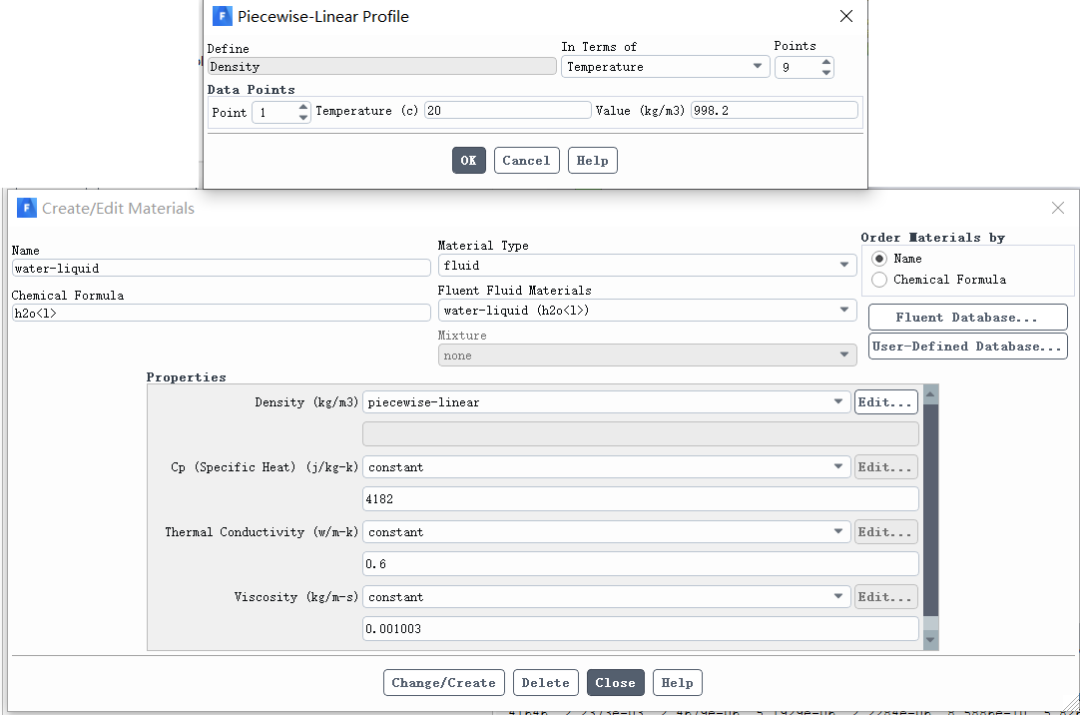
从软件材料库复 制液态水材料，本案例将密度修改为分段线性模型，密度模型的设置是自然对流问题的根本。在很多问题中，采用Boussinesq模型既可以满足计算要求，也具有较好的收敛性。对于比热、导热系数和粘度等物性，本案例按常值考虑，建议实际应用中考虑温度的影响。
 

      对于封闭空间的自然对流问题，将压力的离散格式改为PRESTO!可以获得更为准确的近壁面速度结果。
 

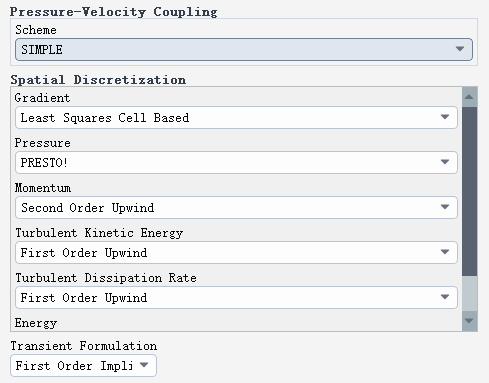
创建两个监视器，分别监测冷源的热功率和回路的质量流量（监测位置为之前建立的内部面）
 

计算时，先用稳态求解一定的迭代步数（比如可计算至残差曲线振荡），后采用瞬态求解（本案例时间步长为0.1s），通过监测量来判断是否达到稳定状态。
 

4 计算结果

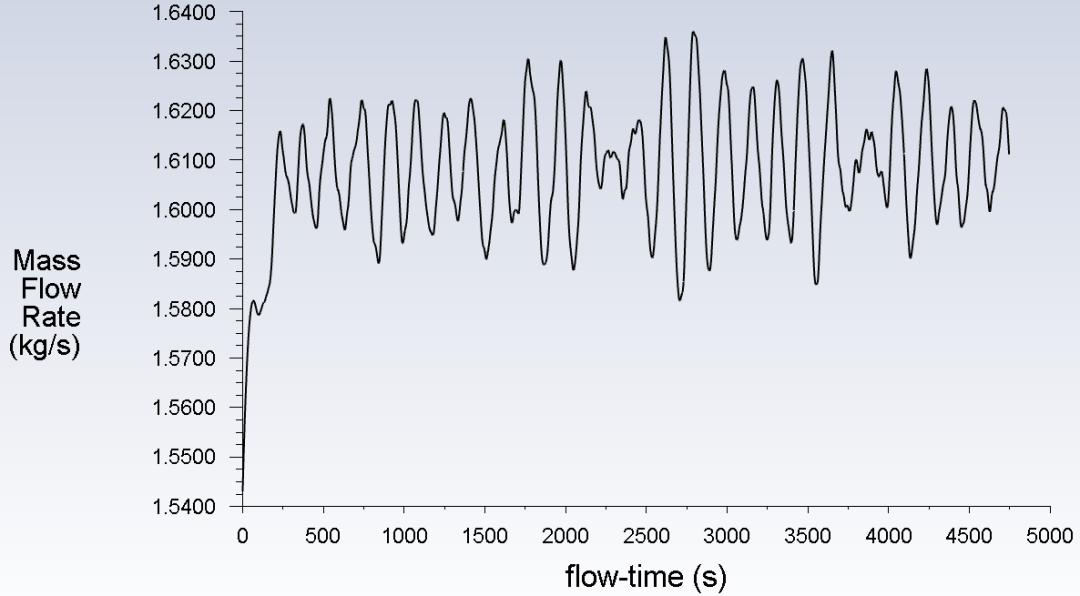
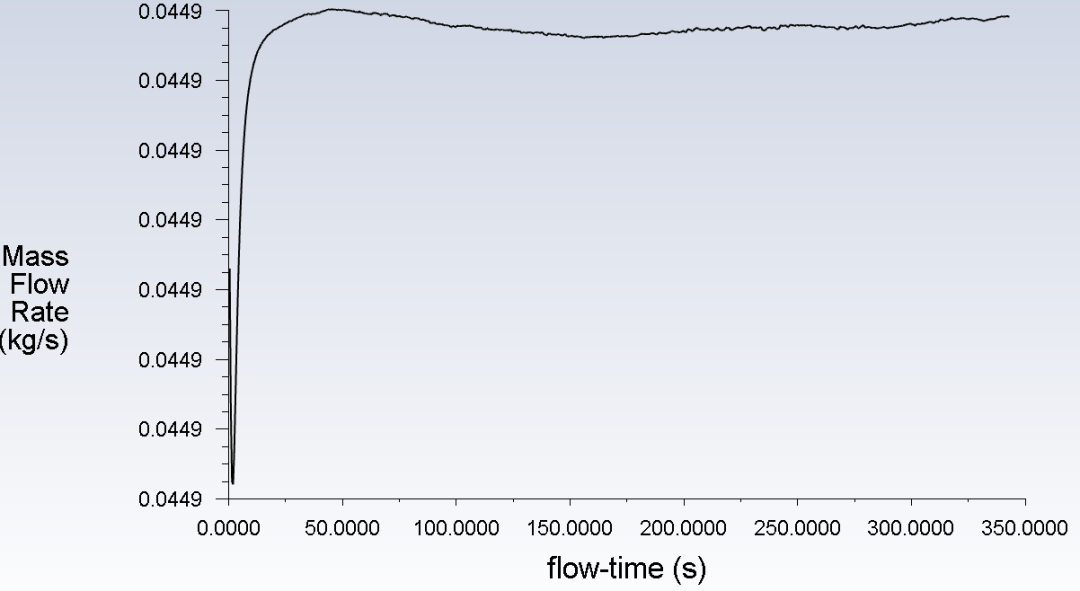
首先，看一下循环流量的监测曲线，基本达到稳定后流量呈现振荡特性。以振荡曲线的中值考虑，循环流量约为1.6kg/s。

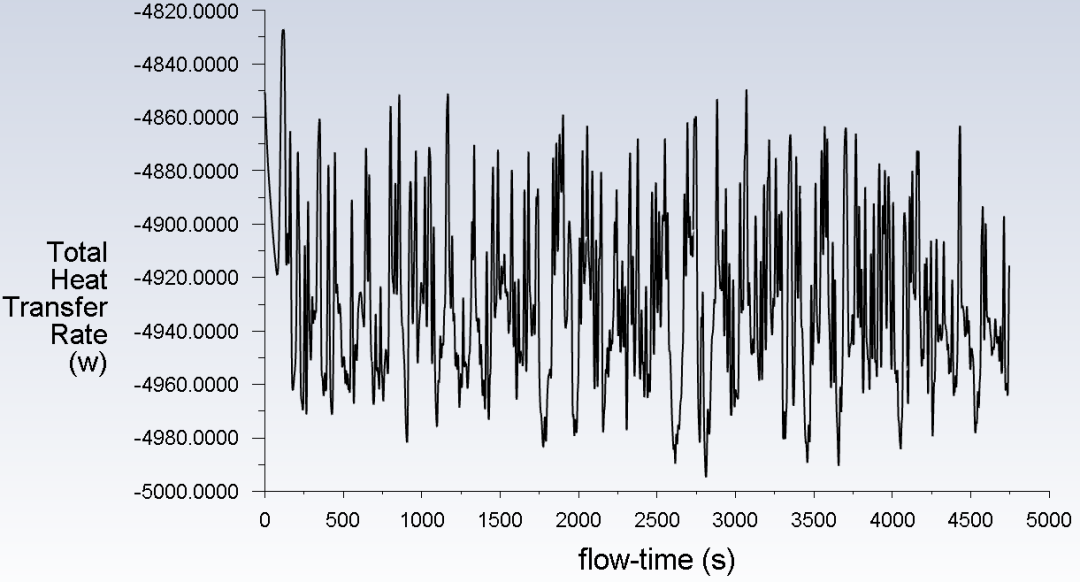
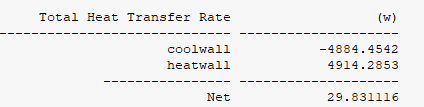
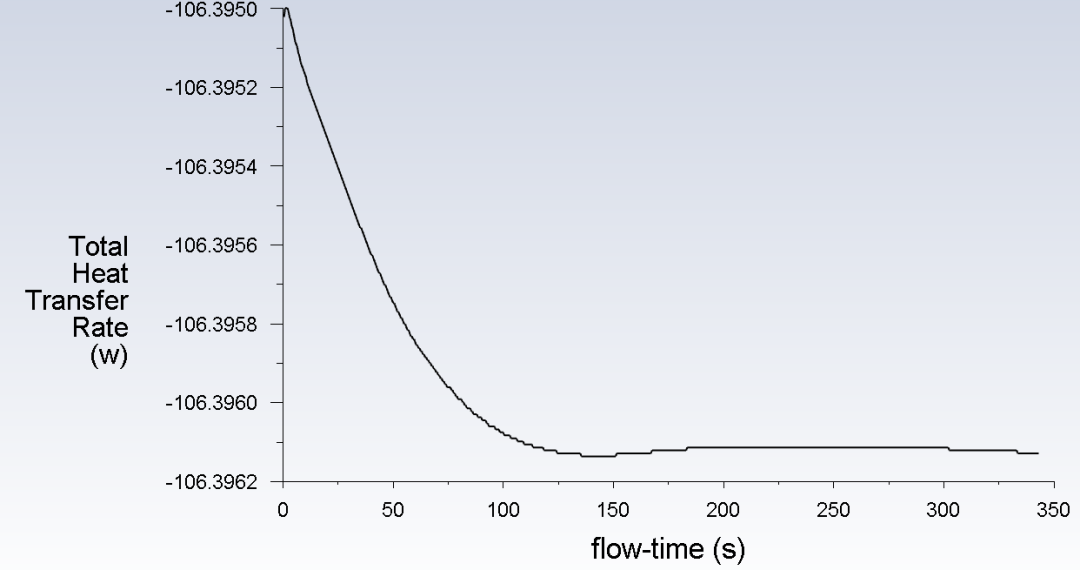
再看一下回路热传输功率的监测曲线，和流量一样，也呈现振荡特性。以振荡曲线的中值考虑，回路热传输功率约为4.95kW，看一下热源和冷源的功率平衡情况，可以看出不平衡率不到1%。

最后看一下回路的速度矢量，介质的流向符合“热上冷下”的实际情况。

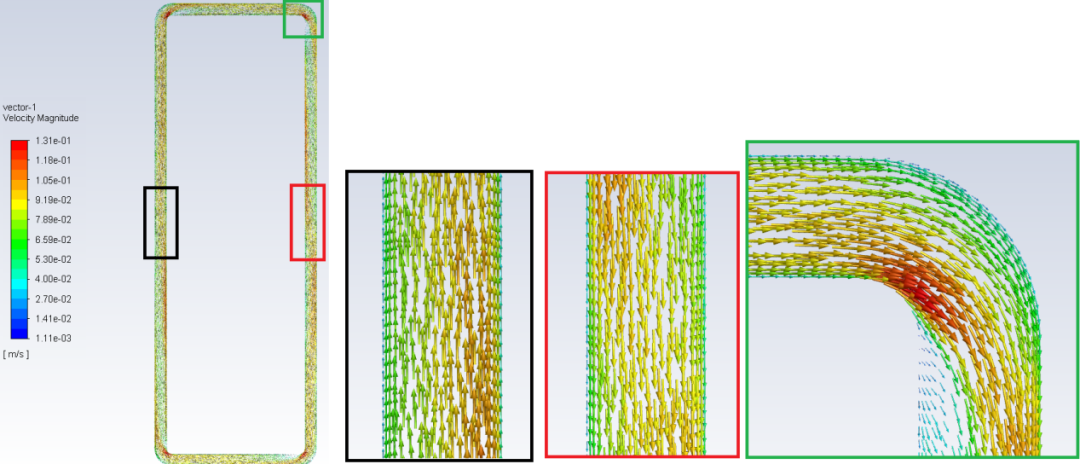
上述的仿真结果中，循环流量呈现的振荡现象称作流动不稳定性，这在自然循环回路中是要尽量避免的。单相自然循环流动不稳定现象的出现, 需要较大的加热功率及合适的阻力系数及系统布置，当存在较大的加热功率和较小的流动阻力时，更容易出现流动不稳定现象[2]。
 

为验证上述观点，我们将热源温度减小到40℃（减小功率），同时增大介质的动力粘度至0.1003Pa·s（增大阻力），此时冷源功率和回路循环流量监测曲线如下。可以看出，流动不稳定性基本上不复存在了。另有研究表明，当热源和冷源的高度差增大时，流动不稳定性通常会增加。因此有可能是本案例的热源和冷源高度差较大造成流动稳定性较差。感兴趣的读者可以自行尝试计算一下，本案例从略。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删