利用Matlab探索大数定律的实际应用

MonteCarlo 方法在数值计算中具有广泛的应用，甚至在非晶的结构的模拟过程中也引入了MonteCarlo 方法，本期过冷水就和大家分享一下Monte Carlo算法。

求解定积分：

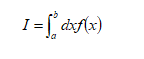
在被积函数f(x)相当复杂时，就只能采取数值积分的求法。并不是所有的复杂的定积分问题的数值解都可以用决定论算法求解。这个时候就可以用Monte Carlo 方法：在（a,b）区域内均匀随机抽样得到N个点x1、x2、x3、...、xN;求这些点上被积函数的值f(x1)、f(x2)、f(x3)......f(xN)、f(x1)、于是f(x)在[a,b]区域的平均值：

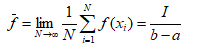
于是定积分：

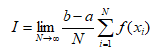
上述过过程实际展现了求平均数的两种不同表述方法。两个公式自然而然就联系起来了，用一个公式计算另一个公式的相关参数。这个过程你都感觉不到统计力学的身影，这就是

Monte Carlo的另一种思想。

过冷水之前以为的Monte Carlo算法是通过随机撒点求所求区域占规则形状的面积比值然后用规则面积*比值即为所求面积面积。我们来实战演示一下两种思路求积分的具体过程。

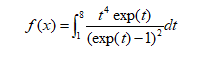
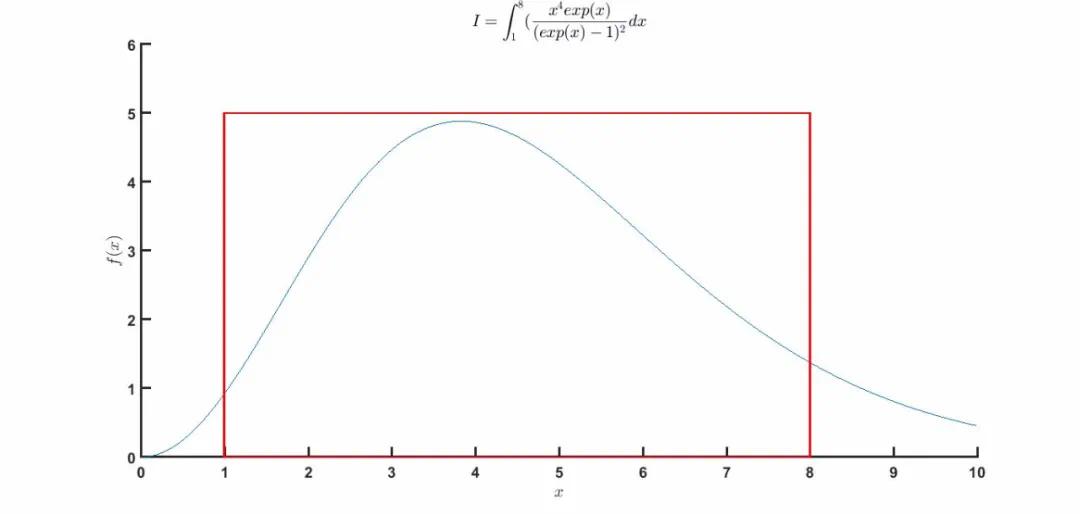
Monte Carlo方法一：概率求积分

warning offfeature jit offn=100000;x=1 7*rand(1,n);y0=5.*rand(1,n);y=(x.^4.*exp(x))./(exp(x)-1).^2;points=find(y0<=y);k=length(points);S=7*5*(k/n)S = 23.2418

Monte Carlo方法二：大数定理求积分

warning offfeature jit offn=100000;x=1 7*rand(1,n);y0=5.*rand(1,n);y=(x.^4.*exp(x))./(exp(x)-1).^2;I=7*sum(y)/nI =   23.2552

符号积分法：

warning offfeature jit offsyms xf=(x.^4.*exp(x))./(exp(x)-1).^2;y=double((int(f,1,8)))y =   23.2667

可以看出三种方法计算的积分值相近，这也说明了Monte Carlo的两种不同计算路径得到的计算值都是可信的。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删