%Membership function for Young People
clear all;
close all;
for k=1:1:1001
x(k)=(k-1)*0.10;
#让k从1变化到1001,增加步长为1
#x(k)根据变换代入到式子中
if x(k)>=0&x(k)<=25
y(k)=1.0;
#如果x(k)大于等于0并且x(k)小于等于25
#就让y(k)=1
else
#否则,就让y(k)等于下面的式子
y(k)=1/(1+((x(k)-25)/5)^2);
end
end
plot(x,y,'k');
#绘制函数图像(x,y)分别对应横纵坐标,而k表示black黑色的线。
xlabel('X Years');ylabel('Degree of membership');
#xlabel表示横轴注释显示内容,ylabel表示纵轴注释显示内容。
Chap3_2
%Membership function
clear all;
close all;
M=6;
#赋值变量M=6
if M==1 %Guassian membership function
#如果M=1
x=0:0.1:10;
#x从0到10进行变化,步长为0.1
y=gaussmf(x,[2 5]);
#gaussmf()功能:模糊逻辑工具箱中内置的高斯曲线隶属度函数。
#函数原型: gaussmf(x,[sig c])
#sig:指代正态分布的标准偏差σ;
#c:指代正态分布中的均值μ
plot(x,y,'k');
#绘制函数图像,并且用黑线表示
xlabel('x');ylabel('y');
elseif M==2 %General Bell membership function
#如果M=2
x=0:0.1:10;
#x从0变化到10,步长为0.1
y=gbellmf(x,[2 4 6]);
#建立一般钟型隶属函数)
#这里x指定变量定义域范围,参数b通常为正,参数c位于曲线中心,第二个参数变量params是一个各项分别为a,b和c的向量。
plot(x,y,'k');
xlabel('x');ylabel('y');
elseif M==3 %S membership function
#或者当m=3时
x=0:0.1:10;
#x从0变化到10,步长为0.1
y=sigmf(x,[2 4]);
#S型隶属函数sigmf(x,[a c])
#sigmoid membership function
#参数a的正负符号决定了S形隶属函数的开口朝做还是朝右,用来表示“正大”或“负大”的概念。
plot(x,y,'k');
xlabel('x');ylabel('y');
elseif M==4 %Trapezoid membership function
#当M等于4时:
x=0:0.1:10;
#x从0变化到10,步长为0.1
y=trapmf(x,[1 5 7 8]);
#梯形隶属函数trapmf(x,[a,b,c,d])
#其中参数a和d确定梯形的“脚”,而参数b和c确定梯形的“肩膀”
plot(x,y,'k');
xlabel('x');ylabel('y');
elseif M==5 %Triangle membership function
#当M=5时
x=0:0.1:10;
#x从0变化到10,步长为0.1
y=trimf(x,[3 6 8]);
#三角形隶属函数trimf(x,[a,b,c])
#其中参数a和c确定三角形的“脚”,而参数b确定三角形的“峰”
plot(x,y,'k');
xlabel('x');ylabel('y');
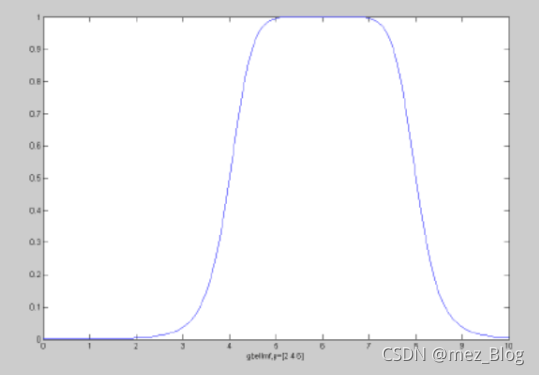
elseif M==6 %Z membership function
#当M=6时
x=0:0.1:10;
#x从0变化到10,步长为0.1
y=zmf(x,[3 7]);
#Z型隶属函数:这是基于样条函数的曲线,因其呈现Z形状而得名。参数a和b确定了曲线的形状。
#zmf(x,[a,b])
plot(x,y,'k');
xlabel('x');ylabel('y');
End
(1)高斯

2.钟型隶属函数





Chap3_3
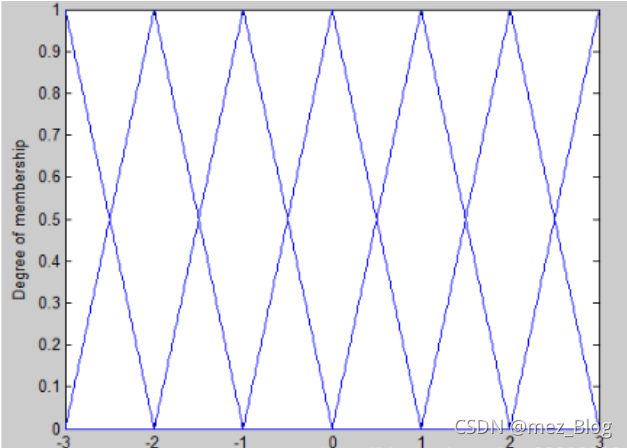
%Define N+1 triangle membership function
#定义N+1个模糊等级
clear all;
close all;
N=6;
x=-3:0.01:3;
#定义x范围为-3~3
for i=1:N+1
#对i来说,从1变化到N+1
f(i)=-3+6/N*(i-1);
end
u=trimf(x,[f(1),f(1),f(2)]);
#三角型隶属函数
#里面的参数就是将i的值代入到上面的公式中,
#最终得到[-3,-3,-2]
figure(1);
# figure(s) % s为参数,s为数据时要大于0,否则报错
#就是MATLAB运行时的窗口的名字,默认为figure 1
plot(x,u);
#进行绘制,横轴x,纵轴u
for j=2:N
#j由2~N
u=trimf(x,[f(j-1),f(j),f(j+1)]);
#同理进行代入,得到结果为[-3 -2 -1]~[1 2 3]
hold on;
#hold on主要是用于添加新绘图的时候保留当前绘图,
主要在绘制多条线的时候用到
plot(x,u);
end
u=trimf(x,[f(N),f(N+1),f(N+1)]);
#得到最终结果为[2,3,3]
hold on;
plot(x,u);
xlabel('x');
ylabel('Degree of membership');
Chap3_4
clear all;
close all;
A=[0.8,0.7;
0.5,0.3];
#2*2的矩阵
B=[0.2,0.4;
0.6,0.9];
#2*2的矩阵
%Compound of A and B
#A和B的化合物
#也就是A圈B
for i=1:2
#i是由1变化成2
for j=1:2
#J是由1变化成2
AB(i,j)=max(min(A(i,:),B(:,j)'))
#0.8与0.2取最小为0.2,0.7与0.6取最小为0.6.最后0.6与0.2取最大为0.6.
#则AB的第一个数为0.6
#min(0.8,0.4)=0.4,min(0.7,0.9)=0.7,最后max(0.4,0.7)=0.7
#然后同理写出第二行的数
#最后A圈B并不改变维数,原来A和B的2*2的矩阵经过结合之后还是变成2*2
#AB(i,j)等于A的第i行与B的第j列取小后取大
end
end
%Compound of B and A
for i=1:2
for j=1:2
BA(i,j)=max(min(B(i,:),A(:,j)'))
#B=[0.2,0.4;
0.6,0.9];
#2*2的矩阵
#A=[0.8,0.7;
0.5,0.3];
#2*2的矩阵
#第一步:0.2和0.8取最小为0.2,0.4和0.5取最小0.4,最后0.4和0.2取最大0.4
#第二步:min(0.2,0.7)=0.2,min(0.4,0.3)=0.3,max(0.2,0.3)=0.3
#同理在第三步和第四步得到0.6和0.6.合并得到最终的B圈A矩阵(2*2)【注:A圈B称为A于B的合成】
end
End

Chap3_5
clear all;
close all;
A=[0.5;1;0.1];
B=[0.1,1,0.6];
C=[0.4,1];
#建立矩阵A,B,C
#A是一个3行1列的矩阵
#B是一个1*3的矩阵
#C是一个1*2的矩阵
%Compound of A and B
for i=1:3
for j=1:3
AB(i,j)=min(A(i),B(j));
#i从1变化到3,j也是从1变化到3
#然后将a或b的每一个的元素分别与b或a的每一个元素进行对比取最小
#也就是任取一个矩阵中的数去对应另一个矩阵中进行一一比较
#最后变成一个3*3的矩阵
end
end
%Transfer to Column
#转成列
T1=[];
for i=1:3
T1=[T1;AB(i,:)'];
#T此时将ab全部转置成一列
end
%Get fuzzy R
for i=1:9
#i从1变化到9
for j=1:2
#j从1变化到2
R(i,j)=min(T1(i),C(j));
#同上面一样T和C的每一个元素进行一一比较,最后形成一个9*2的矩阵
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
A1=[1,0.5,0.1];
B1=[0.1,0.5,1];
#A1(1*3)
#B1(1*3)
for i=1:3
for j=1:3
AB1(i,j)=min(A1(i),B1(j));
#最后变成3*3的最小值矩阵
end
end
%Transfer to Row
T2=[];
for i=1:3
T2=[T2,AB1(i,:)];
#没有了单引号’,此时为一行的输出值
end
%Get output C1
for i=1:9
for j=1:2
D(i,j)=min(T2(i),R(i,j));
#(9*2)
C1(j)=max(D(:,j));
#D是一个9*2的矩阵,而C1是保留列数2,行数对所有的值进行对比
#选出在两列中所对应上的最大值,最终变成了1*2的矩阵
end
end
C1
#C1为一个输出语句

%Fuzzy Control for water tank:水箱的模糊控制
clear all;
close all;
a=newfis('fuzz_tank');
#创建一个 FIS (Fuzzy Inference System模糊推理系统 ) 对象,第一个参数为fis名
%水位变化e划分,NB:负大 NS:负小 Z:零 PS:正小 PB:正大
%向模糊推理系统中添加语言变量
a=addvar(a,'input','e',[-3,3]); %Parameter e 声明了变量e,并且e的取值范围为-3到3. input和output为模糊变量。
#增加模糊语言变量
#addvar函数是用来添加变量到模糊推理系统中的一个函数
#fis = addvar(fis,varType,varName,varBounds)
#fis—MATLAB中的一个模糊推理系统
#varType—要添加到模糊推理系统中的变量的类型,例如’input’ 和 ‘output’
#varName—要添加的变量的名字,一般是一个字符向量或字符串
#varBounds—变量的取值范围,一般是一个二值向量,其中第一个元素是变量可取的最小值,第二个元素是变量可取的最大值
#模糊变量有两类:input 和 output。在每增加模糊变量,都会按顺序分配一个 index,后面要通过该 index 来使用该变量。
%Z形隶属函数
a=addmf(a,'input',1,'NB','zmf',[-3,-1]);
#在模糊变量中加入隶属函数,这里的NB为negative big,zmf为z型隶属函数。
#addmf(a,'varType',varIndex,'mfName','mfType',mfParams)
#a:工作空间中的FIS结构变量名
#vartype:要添加的隶属度函数的变量类型
#varindex为隶属度函数的变量编号
#mfname新添加的隶属度函数名
#mftype:新隶属度函数的类型
#mfparams指定隶属度函数的参数向量;
#增加模糊语言名称,即模糊集合
#每个模糊语言名称从属于一个模糊语言。Fuzzy 工具箱中没有找到离散模糊集合的隶属度表示方法,暂且用插值后的连续函数代替。
#参数 mfType 即隶属度函数(Membership Functions),它可以是 Gaussmf、trimf、trapmf等,也可以是自定义的函数。
#每一个语言名称也会有一个 index,按加入的先后顺序得到,从 1 开始。
%三角形隶属函数
a=addmf(a,'input',1,'NS','trimf',[-3,-1,1]);
a=addmf(a,'input',1,'Z','trimf',[-2,0,2]);
a=addmf(a,'input',1,'PS','trimf',[-1,1,3]);
%S形隶属函数
a=addmf(a,'input',1,'PB','smf',[1,3]);
a=addvar(a,'output','u',[-4,4]); %Parameter u输入参数e的取值范围
#将变量添加到表或时间表中
%控制量u变化划分,NB:负大 NS:负小 Z:零 PS:正小 PB:正大
a=addmf(a,'output',1,'NB','zmf',[-4,-1]);
a=addmf(a,'output',1,'NS','trimf',[-4,-2,1]);
a=addmf(a,'output',1,'Z','trimf',[-2,0,2]);
a=addmf(a,'output',1,'PS','trimf',[-1,2,4]);
a=addmf(a,'output',1,'PB','smf',[1,4]);
%模糊规则
%若e负大,则u负大
%若e负小,则u负小
%若e为零,则u为零
%若e正小,则u正小
%若e正大,则u正大
rulelist=[ 1 1 1 1; %Edit rule base编辑规则库
2 2 1 1;
3 3 1 1;
4 4 1 1;
5 5 1 1];

#这里表示1个输入,一个输出,后面两个为每条规则的权重和条件关系。
a=addrule(a,rulelist);
#增加控制规则,即模糊推理的规则
#其中 ruleList 是一个矩阵,每一行为一条规则,他们之间是 ALSO 的关系。
#假定该 FIS 有 N 个输入和 M 个输出,则每行有 N+M+2 个元素,前 N 个数分别表示 N 个输入变量的某一个语言名称的 index,没有的话用 0 表示,后面的 M 个数也类似,最后两个分别表示该条规则的权重和个条件的关系,1 表示 AND,2 表示 OR。
#例如,当“输入1” 为“名称1” 和 “输入2” 为“名称3” 时,输出为 “ 输出1” 的“状态2”,则写为:[1 3 2 1 1]
a1=setfis(a,'DefuzzMethod','mom'); %Defuzzy设置解模糊方法
%将DefuzzMethod属性设置为mom
#setfis(a,‘fispropname’,‘newfisprop’) 设置模糊系统的属性
# a:为模糊规则库
# fispropname:表示你要设置FIS域属性的一个字符串:
# name,type,andmethod,ormethod,impmethod,aggmethod,defuzzmethod
# newfisprop:你要设置的FIS的属性或方法名称的一个字符串
%保存文件到磁盘上
writefis(a1,'tank'); %Save to fuzzy file "tank.fis"保存模糊规则
a2=readfis('tank'); %从磁盘读出保存的模糊系统
figure(1);%图形1
# figure(s) % s为参数,s为数据时要大于0,否则报错
plotfis(a2);%画图 绘制隶属度函数
%绘制FIS系统结构
#隶属函数图像。
#绘制FIS系统结构
#此函数显示由fismat指定的一个FIS的高层方框图,输入和它们的隶属函数出现在结构特
#征图的左边,同时输出和它们的隶属函数出现在结构特征图的右边。
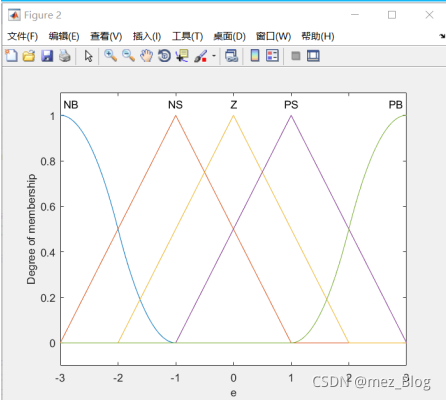
figure(2);%图形2
plotmf(a,'input',1);%画图
#画出隶属度函数图
#%%根据输入变量个数自行确定
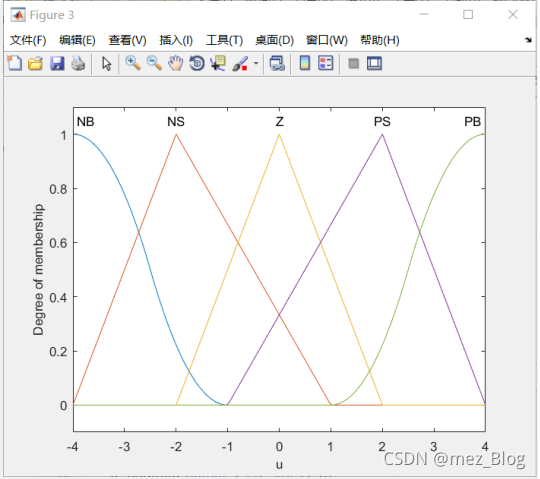
figure(3);%图形3
plotmf(a,'output',1);%画图
flag=1;%设标志位1
if flag==1%如果标志位为1
showrule(a) %Show fuzzy rule base显示模糊规则库【在控制台输出模糊规则】
#showrule(fis,indexList,format) 用于显示与给定系统相关的规则
ruleview('tank'); %Dynamic Simulation动态模拟 开放规则查看器
#打开规则查看器并加载模糊推理系统fis.
end%结束
disp('-------------------------------------------------------');
#disp函数会直接将内容输出在Matlab命令窗口中
disp(' fuzzy controller table:e=[-3,+3],u=[-4,+4] ');
disp('-------------------------------------------------------');
for i=1:1:7 #声明i从1变化到7
e(i)=i-4; #e(i)=-3到3
Ulist(i)=evalfis([e(i)],a2);
#evalfis(input,fismat, numPts)
#input :指定输入值的一个数或一个矩阵,如果输入是一个 M× N 矩阵,其中 N 是输入变量数,那么 evalfis 使用 input 的每一行作为一个输入向量,并且为变量 output 返回 M × L 矩阵,该矩阵每一行是一个向量并且 L 是输出变量数;
#fismat :要计算的一个 FIS 结构;
#numPts :一个可选变量,它表示在输入或输出范围内的采样点数,在这些点上计算隶属函数,如果 不使用此变量,就使 用 101 点的缺省值。
#evalfis(input,fismat)
#给定输入,得到输出,即进行模糊推理。
#其中 fismat 为前面建立的那个 FIS 对象。
end#结束
Ulist=round(Ulist) #round()四舍五入为最近的小数或整数
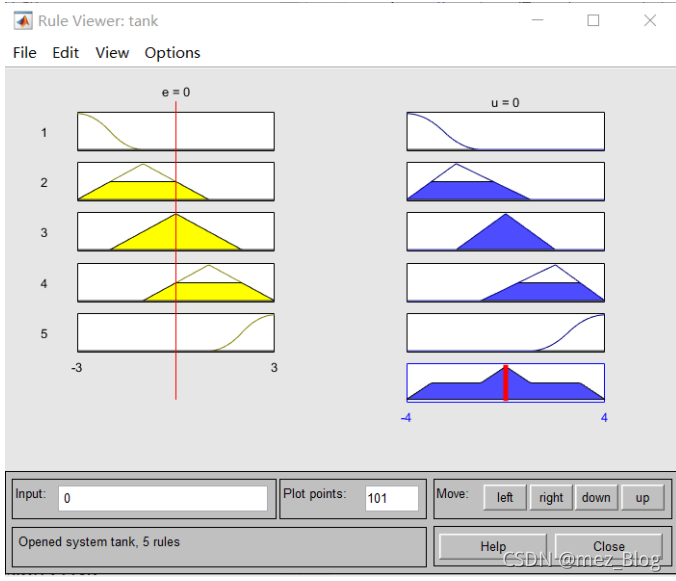
e=-3; % Error出错
u=evalfis([e],a2) %Using fuzzy inference利用模糊推理
选择液位差为e,分为5个模糊集:NB:负大 NS:负小 Z:零 PS:正小 PB:正大,将偏差e的变化分为7个等级:-3,-2,-1,0,1,2,3
控制量u:分为5个模糊集:NB:负大 NS:负小 Z:零 PS:正小 PB:正大,将偏差e的变化分为7个等级:-4,-3,-2,-1,0,1,2,3,4
水位变化e划分表:


控制台输出:
>> chap4_1
ans =
1. If (e is NB) then (u is NB) (1)
2. If (e is NS) then (u is NS) (1)
3. If (e is Z) then (u is Z) (1)
4. If (e is PS) then (u is PS) (1)
5. If (e is PB) then (u is PB) (1)
-------------------------------------------------------
fuzzy controller table:e=[-3,+3],u=[-4,+4]
-------------------------------------------------------
Ulist =
-4 -2 -2 0 2 2 4
u =
-4
>>
最后两行的Ulist输出是u值的输出,当我们的e从-3变化到3时,Ulist就会对应发生值的变化。最后的u的值是因为我们在最后把e赋值为-3,所以对应图像的最左边的u的值,也就是-4.
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删