Matlab简单入门指南

一、help和doc命令

help和doc命令能帮助我们在不知道陌生的函数时，查询到我们函数的说明文档

help函数能帮助我们直接在命令区简洁地显示我们想要查询的函数的命令

help logspace

doc logspace

doc命令能够帮助我们打开某一个函数的详细的信息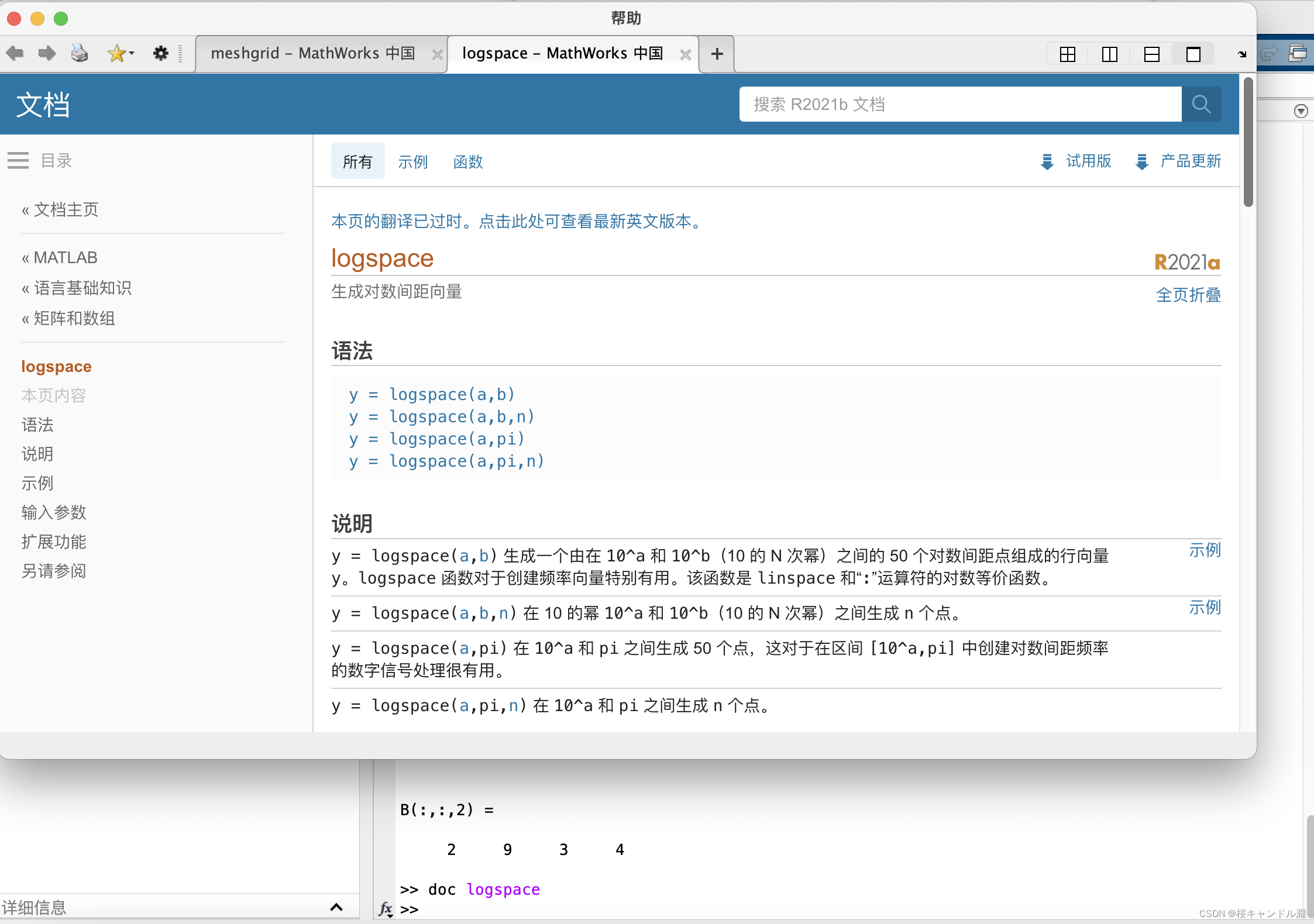

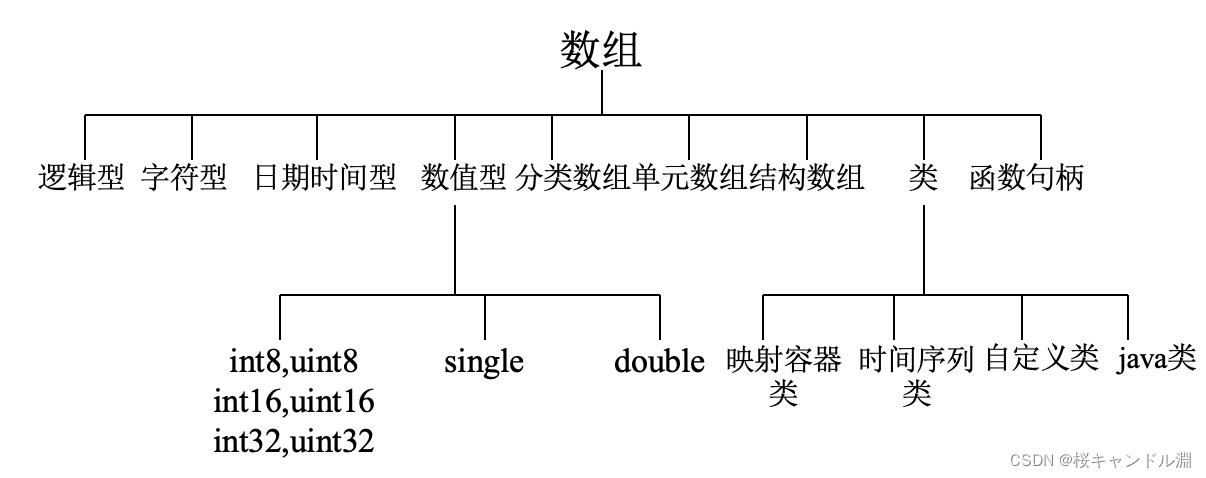
二、数组

在MATLAB中所有的数据都以数组的形式保存

1.常数

2.变量

MATLAB变量的第一个必须是字母

MATLAB区分大小写（a与A是不同的变量）

3.向量

1.直接构造法

a=[1 2 3 4 5 6 7]

2.增量方法构造向量

增量法的第一个数据为初始值，第二个数据为步长，第三个数据为结束值。

a=1:2:10b=10:-2:1

3.使用linspac构造向量

linspace第一个参数为 初始值，第二个值为结束值，第三个值为生成的向量中的元素个数是按照等间隔的方式构造的向量

c=linspace(10,1,20)

4.使用logspace构造向量

第一个参数为10^first，第二个参数为10^last，第三个参数为生成的元素个数

x=logspace(0,1,10)

三、矩阵

1.简单的创建方法

我们在创建矩阵的时候使用分号来分隔，但是我们必须保证每一行的元素个数是相同的。

a=[1,2,3;4,5,6;7,8,9]

2.使用meshgrid构造矩阵

此 MATLAB 函数 基于向量 x 和 y 中包含的坐标返回二维网格坐标。X 是一个矩阵，每一行是x 的一个副本；Y 也是一个矩阵，每一列是 y 的一个副本。坐标 X 和 Y 表示的网格有 length(y) 个行和 length(x) 个列。 [X,Y] = meshgrid(x,y) [X,Y] = meshgrid(x) [X,Y,Z] = meshgrid(x,y,z) [X,Y,Z] = meshgrid(x)

3.构造特殊矩阵

4.聚合矩阵

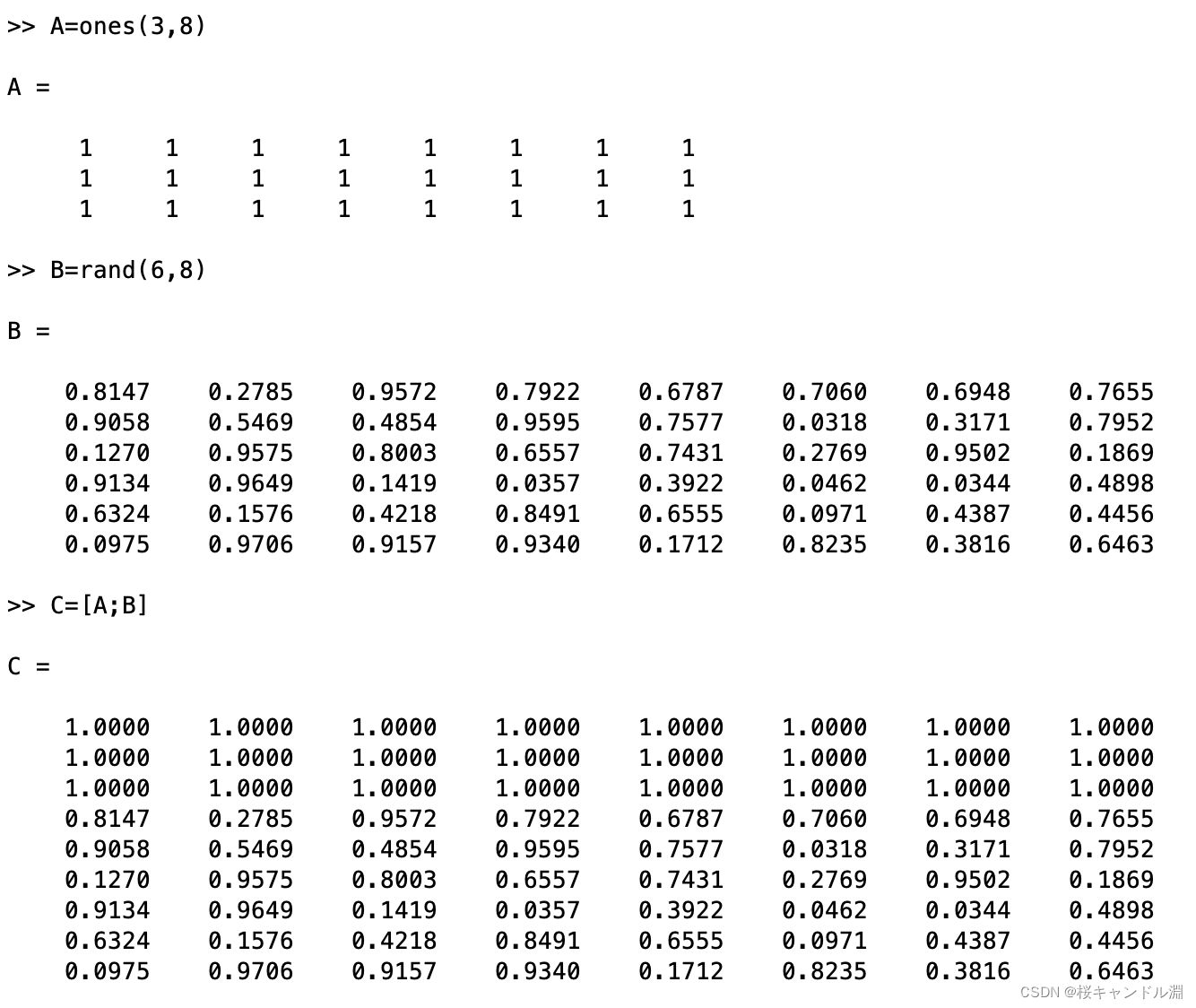
在下面的代码中，我们使用了C来将A于B上下拼接在一起。

在组合不同矩阵的时候，高精度的矩阵和低精度的矩阵进行组合的时候新的矩阵是低精度的。

5.描述数组和矩阵

•大小 – size函数 •最大维的长度- length函数 •维数 – ndims函数 •元素个数 – numel函数

6.排序、反转、转置、重塑

•排序 - sort/sortrows函数 •翻转 – flip/fliplr/flipud函数 •转置 – rot90/transpose函数 •重塑 – reshape, squeeze函数

​​​​​​​

7.获取矩阵的元素

•使用编号索引 •使用线性索引 •使用冒号 •使用end关键字

1.编号索引

2.线性索引

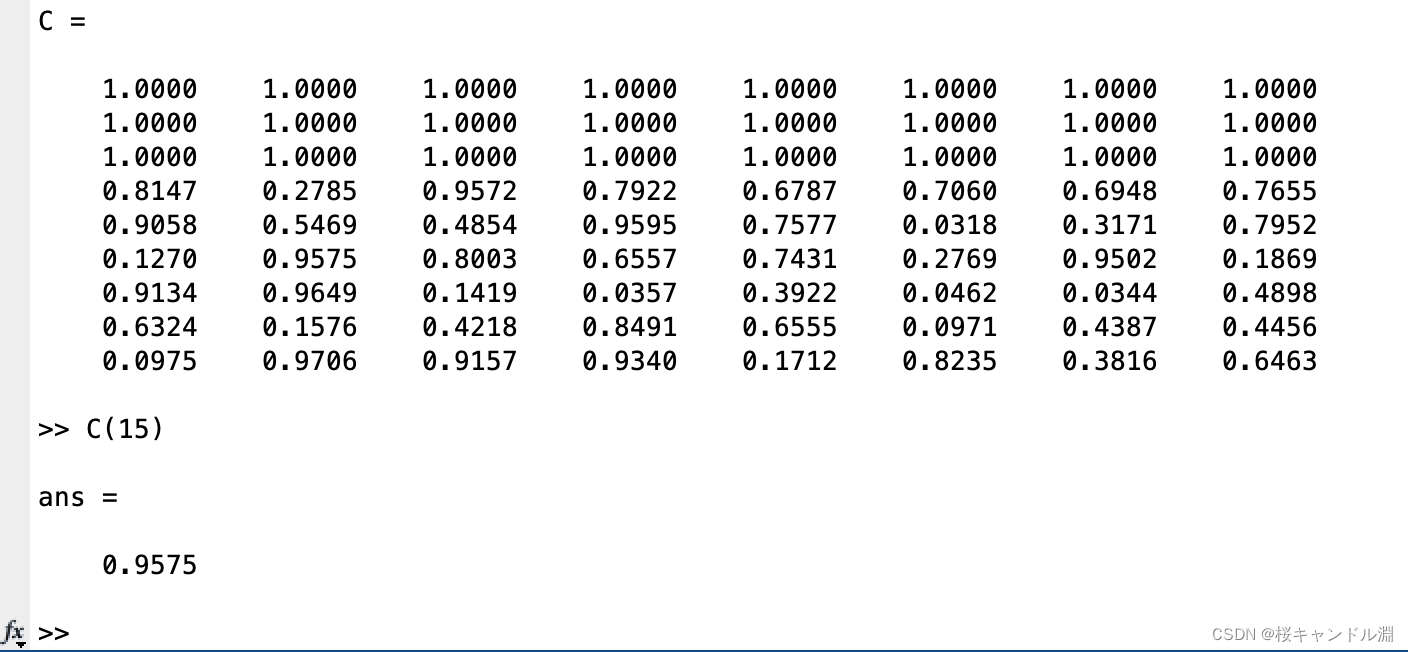
由于MATLAB在保存数组的时候是按照列进行保存的，所以我们在进行线性索引的时候需要按照列进行计算。

在下面的代码中我们看到我们所查找的是C(15)我们首先查找的是第一列，第一列一共有9个元素，所以我们在第二列的第六个元素就是我们的C(15)

3.使用冒号

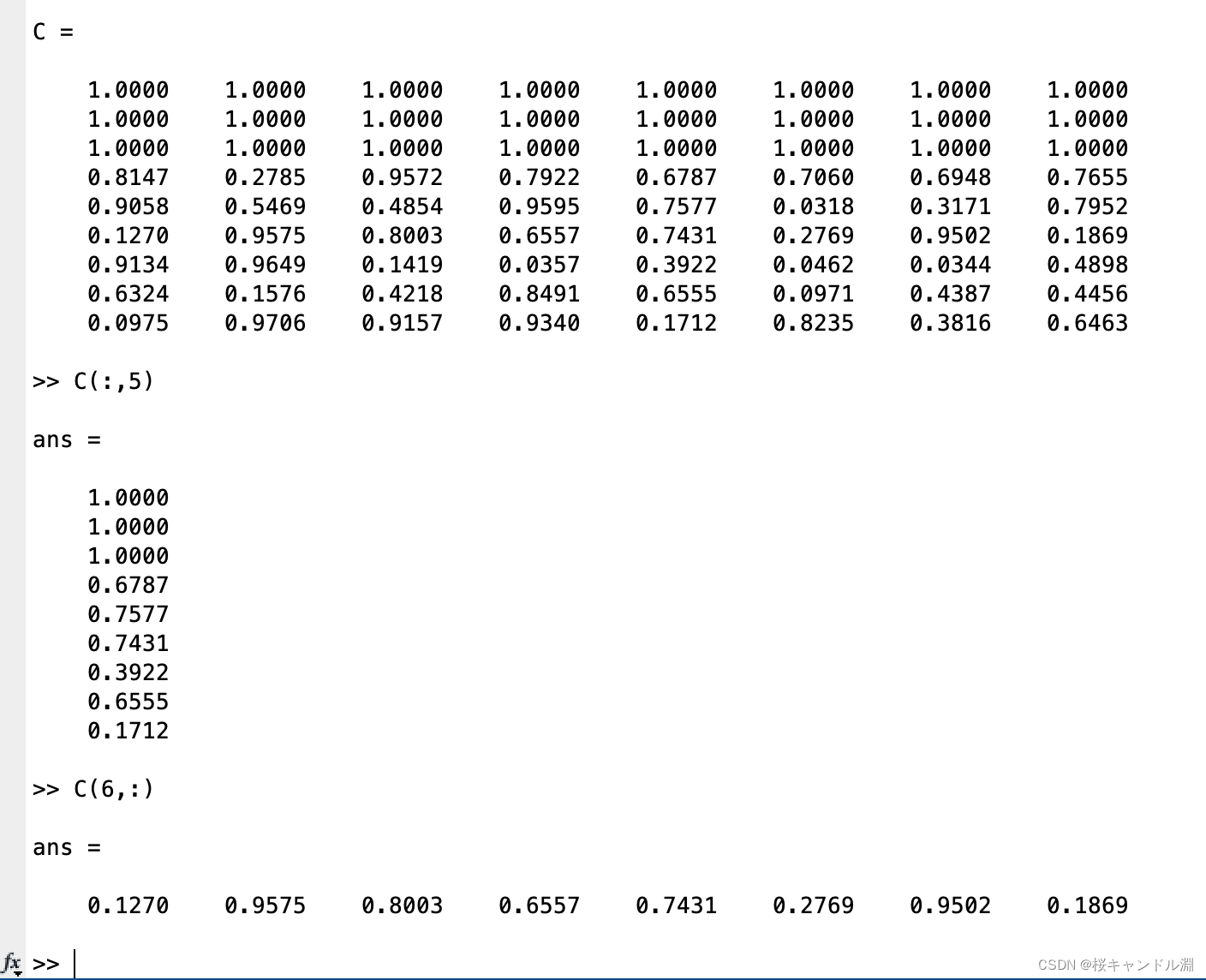
使用冒号可以获取某一行或者某一列的全部元素，或者整个数组本身。

4.使用end关键字来获取矩阵的元素

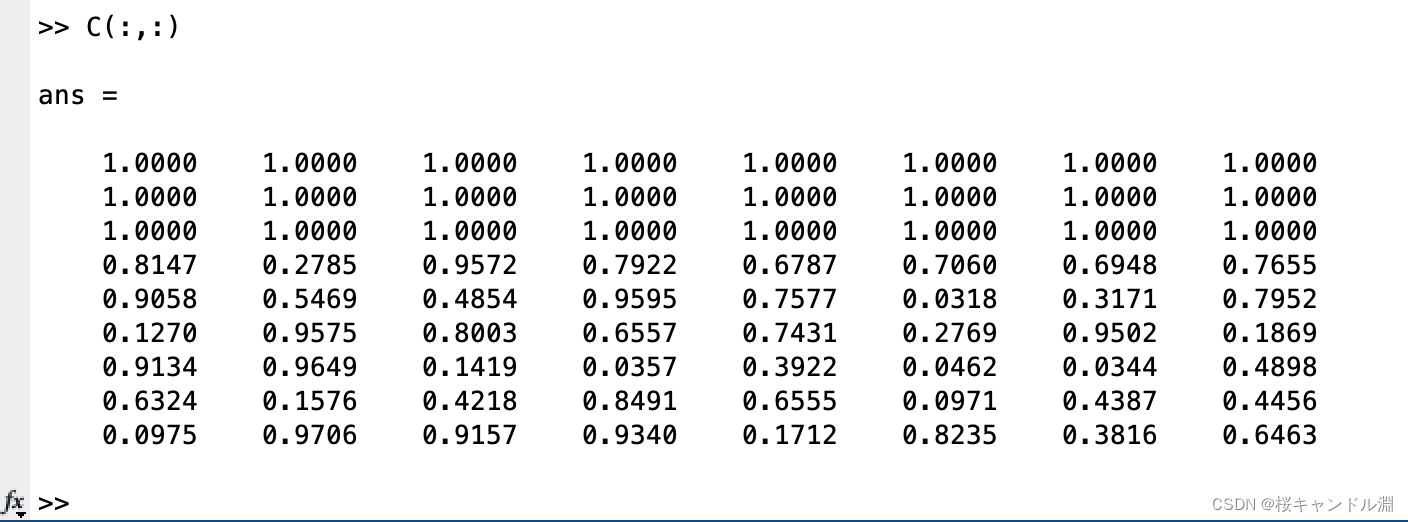
这里的end就表示我们的最后一个元素，然后我们是从1开始取值，到结尾，步长为3，获得我们所有的数据

C(1:3:end)

8.多维数组

1.创建一个正态分布的随机数组

在下面的代码中，我们所生成的就是一个5×3×2的三维数组

2.生成一个元素均为同一常数的数组

3.使用cat生成多维数组

四、数据类型

变量的数据类型 double型数值类型 非double型数值类型 字符串 日期和时间数组 分类数组 表 时间表 结构数组 单元数组 函数句柄

1.字符串

•字符串的创建 •字符串的比较 •字符串的聚合 •字符串的搜索和替换

1.创建字符串

在创建字符串的时候，使用单引号或者是双引号都是可以的。

当然我们也可以创建二维的字符串，但是每一行字符串的元素个数需要相同，并且我们可以使用二维数组的索引来操作我们的二维字符串。

2.类型转换

使用mat2str函数将数组转换为字符串

使用int2str函数将整型数据转换为字符串类型数据

2.函数句柄

函数句柄用于保存MATLAB中所有与函数运行有关的信息

这里我们定义了一个函数（.表示点乘，也就是对我们矩阵中的每一个元素进行处理。）

所以下面的代码所表示的函数为

function f=myfun(x)f=(3-2.*x).^2.*x;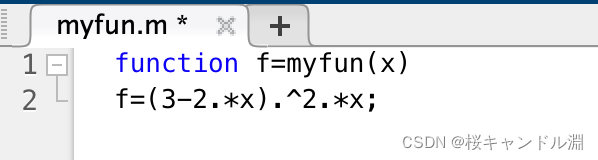

x=fminbnd(@myfun,0,1.5)

在上面的代码中，我们实现了将0和1.5传入我们上述的方法中，然后寻找最小值的过程，然后我们就能够得到我们的x值为1.4999

五、M文件设计

变量 表达式 流程控制 函数 M文件 程序调试与错误处理

1.变量

局部变量：局部变量的作用范围仅限于本函数 全局变量：全局变量用global关键字进行声明，其作用范围为整个M文件

2.表达式

•数值表示 •运算符 •处理字符串表达式

3.数值表示

MATLAB使用传统的数值表示方法。对于比较长的数，使用科学计数法，用字母e指定以10为底的幂次。虚数用i或j作为后缀。

4.运算符

•算术运算符 •关系运算符 •逻辑运算符 •运算符的优先级

1.算术运算符

2.关系运算符

3.逻辑运算符

xor函数的演示

4.运算符的优先级

•小括号() •转置(.')、幂(.^)、复数共轭转置(')、矩阵的幂(^) •一元的加(+)、一元的减(-)、逻辑否(~) •乘(.*)、右除(./)、左除(.\)、矩阵乘(*)、矩阵右除(/)、矩阵左除(\) •加(+)、减(-) •冒号操作符(:) •小于(<)、小于或等于(<=)、大于(>)、大于或等于(>=)、等于(==)、不等于(~=) •逐元素AND(&) •逐元素OR(|) •&& •||

5.流程控制

•条件控制 •循环控制 •程序终止控制

1.条件控制

这里我们定义了一个流程控制的函数。

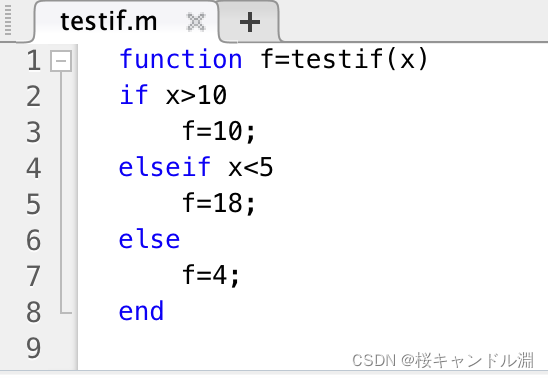
这是我们测试的结果

当然我也可以通过Switch-case语句来实现流程控制

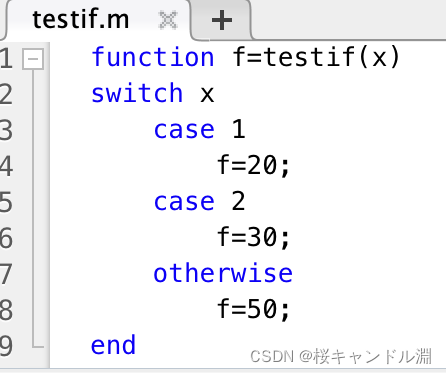
2.循环控制

for循环 while循环

for循环

while循环

function f=testif(x)sum=1;while(x>=1)    sum=sum*x;    x=x-1;f=sum;end

3.程序终止控制

六.函数

1.匿名函数

匿名函数在实现一些简单的函数的时候能够快速地实现

fhandle=@(arglist) expr

2.检查输入参数的个数

使用nargin可以确定函数输入的参数的个数,nargout函数可以确定输出参数的个数

function c = w(a, b)  if (nargin == 1)      c = 1;  elseif (nargin == 2)      c = 2;  end

3.函数句柄

句柄函数可以让我们的函数用一个简单的变量去使用

function c = w(x) c=sin(x);end

在下面的代码中，我们将w方法传递给了我们的x

然后当我们可以通过feval函数，第一个参数传入我们的方法，第二个参数传入我们的具体的自变量。

当然我们也可以传入一串数据来进行批量计算

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删