想来大家看到题目,从事质量行业的朋友,脑海里回直接跳出Minitab来计算Cpk/Ppk的页面:
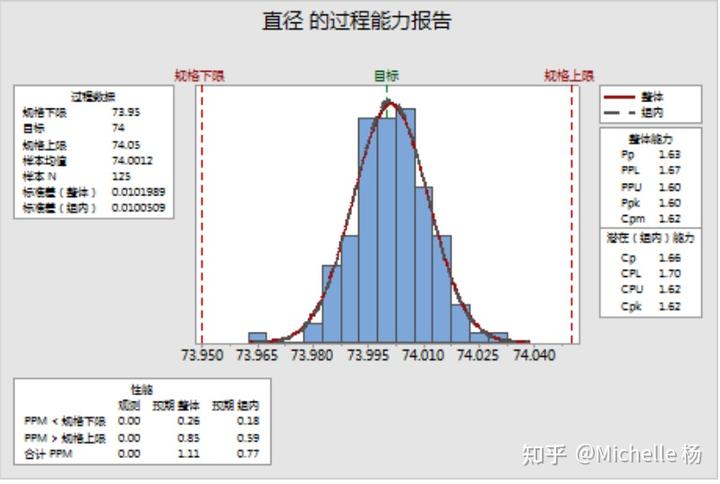
图1 Minitab中过程能力分析的示例图
在图1的左下方,大家可以得到PPM数值,同样,在右上方可以看到过程能力数值。
但今天我们主要讨论的是,通过Cpk/Ppk直接计算PPM。下表是比较常见Cpk和PPM的对应表,在网站或者质量手册上都可以查到。那如果是非常见的Cpk数值呢?比如是0.45,0.8,1.4。接下来小编会分享一种利用Minitab来计算的方法。
| Cpk | 西格玛水平 | 合格率 | PPM(百万故障失效率) |
| 0.33 | 1.0 | 68.27% | 317311 |
| 0.67 | 2.0 | 95.45% | 455000 |
| 1.00 | 3.0 | 99.73% | 2700 |
| 1.33 | 4.0 | 99.9937% | 63.3 |
| 1.67 | 5.0 | 99.999943% | 0.570 |
| 2.00 | 6.0 | 99.9999998% | 0.002 |
我们先来复习下Cpk的公示,(在这里大家先忽略Cpk/Ppk 中变差Sigma的计算方式)
Cpk=\frac{min(UCL-\bar{x}),(\bar{x}-LCL)}{3\sigma}Cpk=\frac{min(UCL-\bar{x}),(\bar{x}-LCL)}{3\sigma}
Cp=\frac{UCL-LCL}{6sigma}Cp=\frac{UCL-LCL}{6sigma}
在这里,无关具体应用,我们可以假设 \bar{x}=0,\sigma=1\bar{x}=0,\sigma=1 ,且UCL和LCL对称,即标准正态分布,经过公示换算,可以得到: Cp=CpkCp=Cpk
当 UCL-LCL=2\sigma,Cpk=0.33,西格玛水平1.0UCL-LCL=2\sigma,Cpk=0.33,西格玛水平1.0 ;
UCL-LCL=6\sigma,Cpk=1.0,西格玛水平3.0UCL-LCL=6\sigma,Cpk=1.0,西格玛水平3.0 。
接下来,正式进入合格率/失效率的计算:
1.1 步骤1,选择计算-概率分布-正态
1.2 步骤2,选择累积概率
1.3 步骤3,输入常量,这里输入3,得到结果0.998650,对应图4中左边的图形面积,右边面积可以理解是不良率0.00135,考虑双边不良率则是0.0027,即百万故障不良率PPM是2700.

图2 Minitab的输入操作
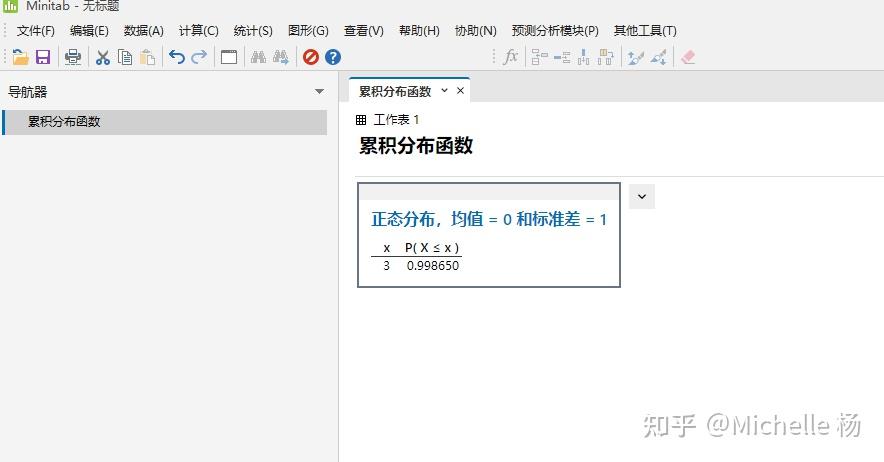
图3 Minitab显示计算结果
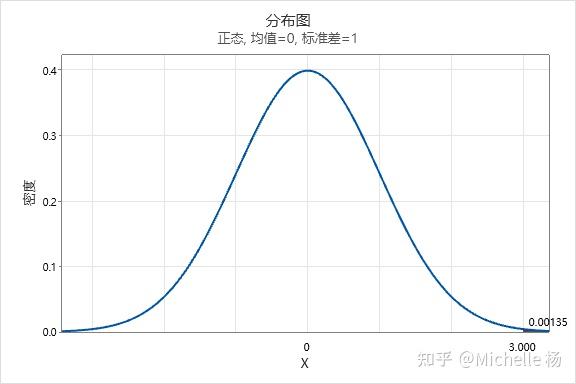
图4 minitab概率图显示单边0.00135对应3西格玛水平
为了更直接地得到失效率,我们可以在西格玛水平处输入负数(对称),得到单边失效率0.00135,最终结果需要乘以2.

图5 Minitab显示西格玛水平是-3时,对应失效率
接下来我们计算任一Cpk,比如, Cpk=0.4Cpk=0.4 ,
有 西格玛水平=3Cpk=3\times0.4=1.2西格玛水平=3Cpk=3\times0.4=1.2
在minitab中,输入常量-1.2,得到单边失效率0.115,那么其百万故障不良率是230000.

图6 输入常量-1.2的单边不良率计算
同样,我们可以计算出其它任意Cpk或者西格玛水平的不良率/PPM值。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删