Minitab学习：CPK、PPK案例分析

前言

一、认识CPK

在SPC(统计过程控制中)，主要分为：

• 控制图：是对过程的一种监控，预测，用于观察过程运行趋势，提前预防不良发生(控制图中的控制限是过程输出的，通过过程计算出来的)；
• 过程能力分析：是对过程进行检测，探测过程中将有多少不良发生(过程能力分析中的规格上下限是标准给出的，不随过程变动而变动)；
  
      CPK：过程能力指数(短期过程能力指数)
  
      PPK：过程性能指数(长期过程性能指数)

正态分析

包括二项过程能力，DPMO、PPM、Z值等均属于过程能力分析，在SPC手册中：过程能力由造成变差的普通原因来确定，通常代表过程本身的最佳性能；在处于统计控制状态下运行过程，一般来说，由于受统计控制的过程服从可预测的分布，从该分布中可以估计出符合规范的产品比例。

计算CPK前提：

1. 过程应该处于统计控制状态，并且变差是由普通原因造成，换而言之，在进行过程能力分析之前，应该确定该过程是否受控，控制图中是否有异常因素；
2. “服从可预测分布”，例如：正态分布(二项过程能力应该服从二项分布)；
3. 数据独立：在分析CPK之前，数据应该服从正态分布，过程应该稳定受控并且数据收集过程应该独立。

除了上述三个条件外，数据收集应该满足时间顺序，分析见（三、时间顺序对CPK的影响）

二、实例应用

1.数据收集

分为25个组，每组5个数据

2.minitab CPK入口

分析之前需要将数据进行转置处理，minitab中数据在多列时，每组数据占一行；或将所有数据堆叠到一列中；
进入入口1：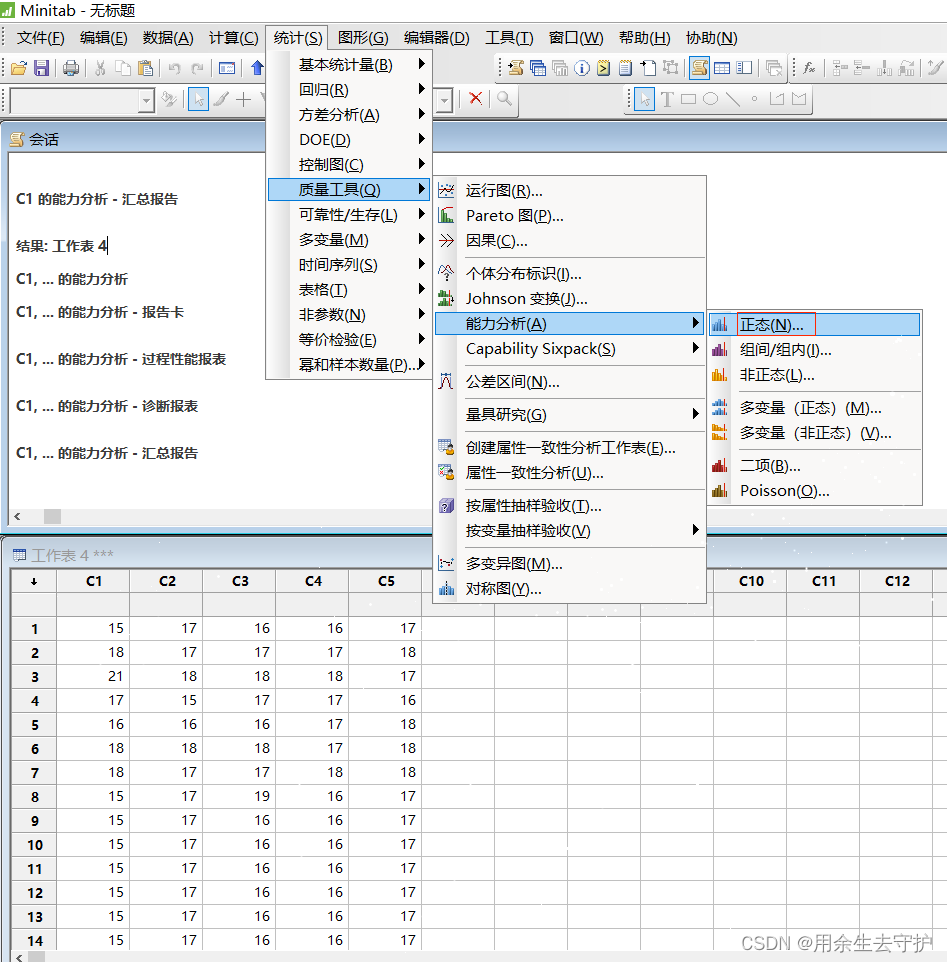

进入入口2：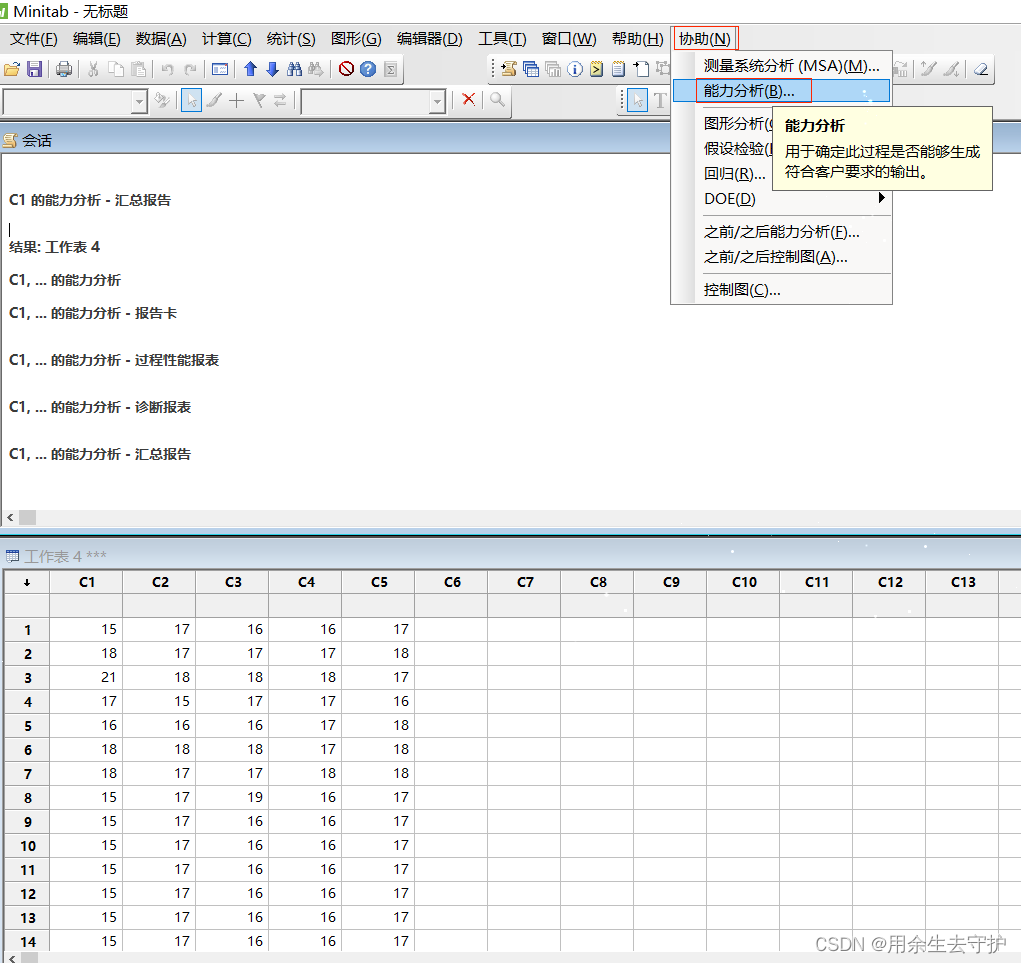

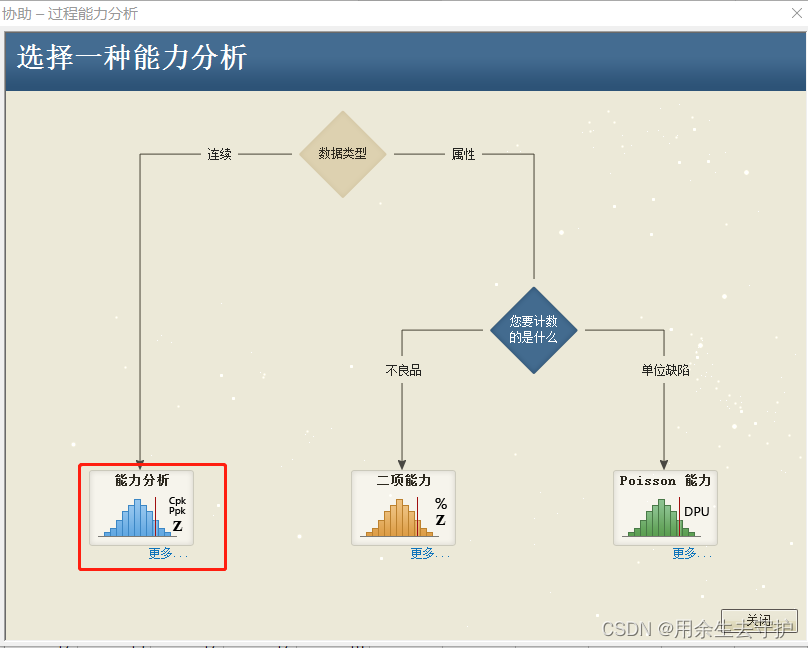
3.CPK参数设置

入口1：

   单列：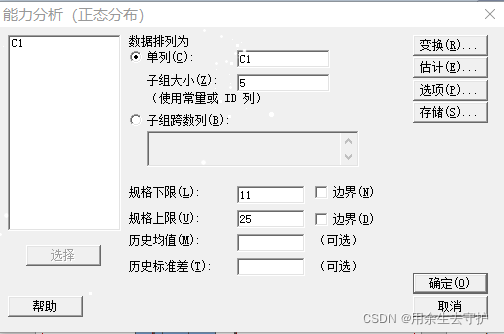

多列：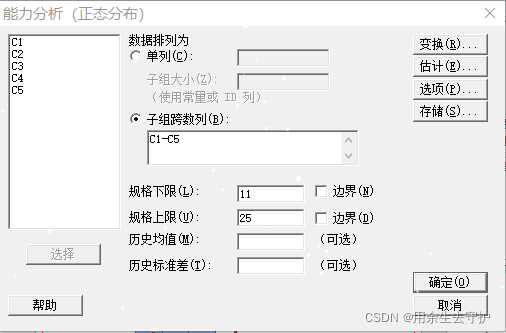

入口2：

   单列：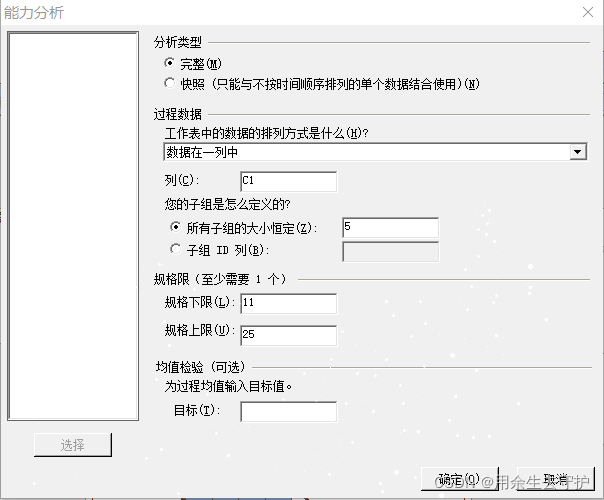


   多列：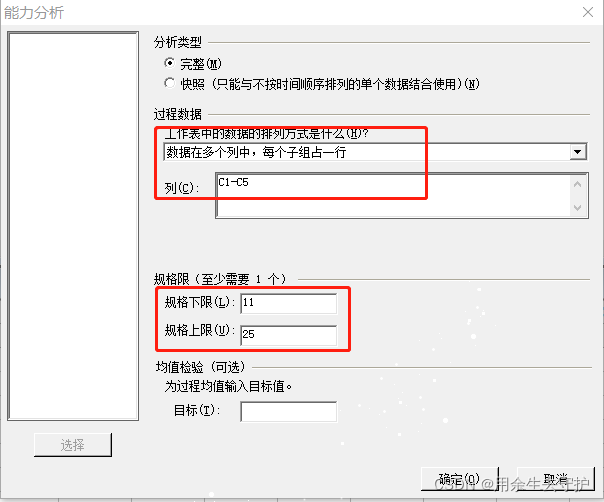

4.生成图形

入口1：

   单列：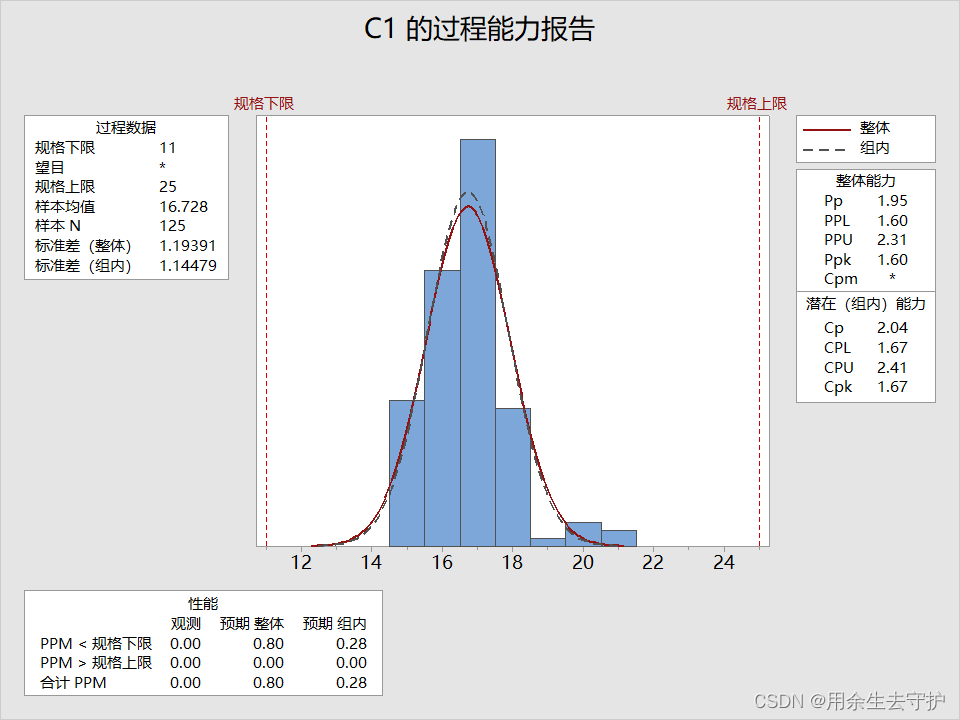


   多列：

入口2：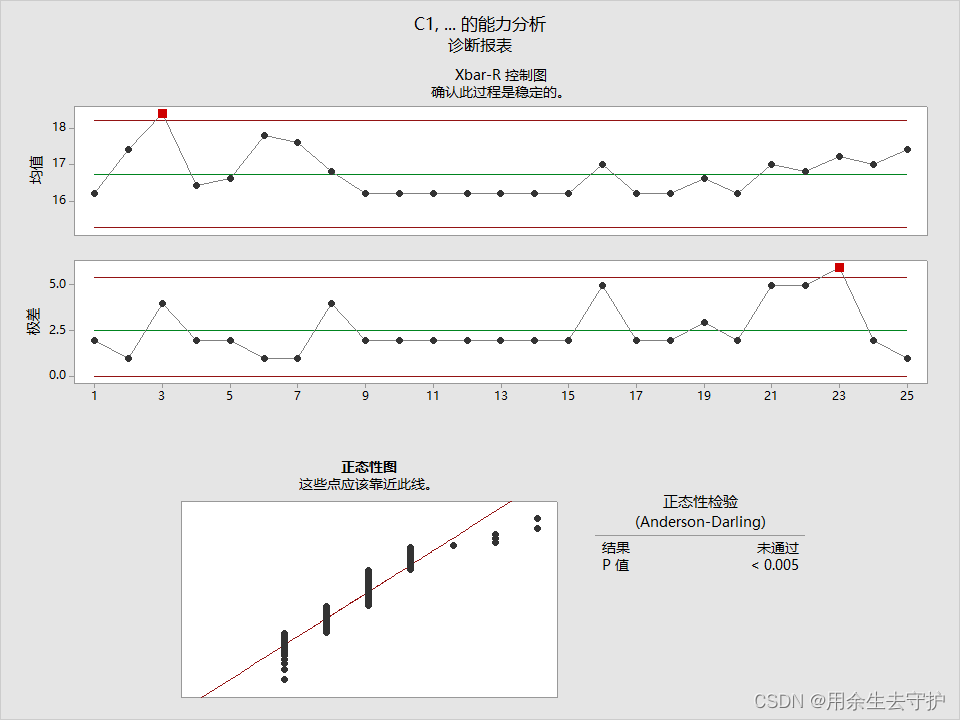

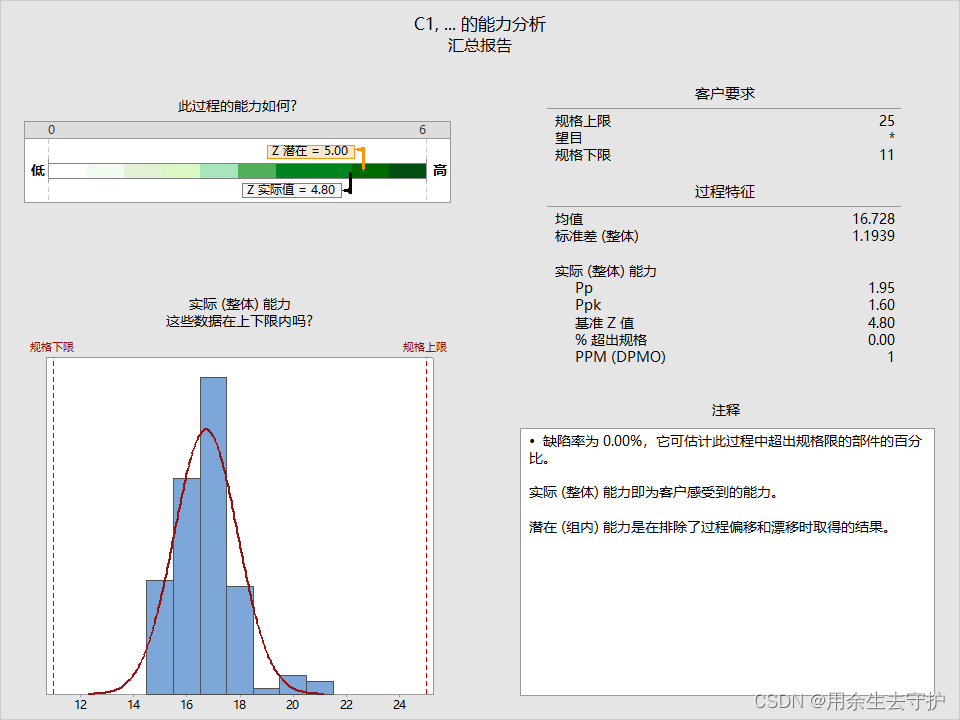
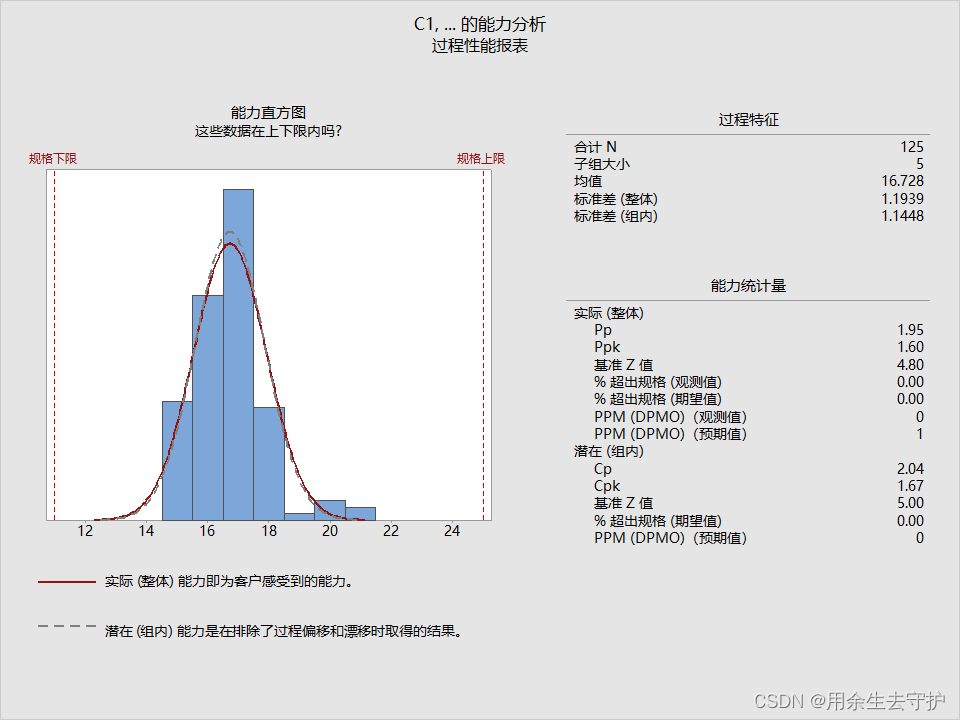
三、时间顺序对CPK的影响

当对数据进行排序后：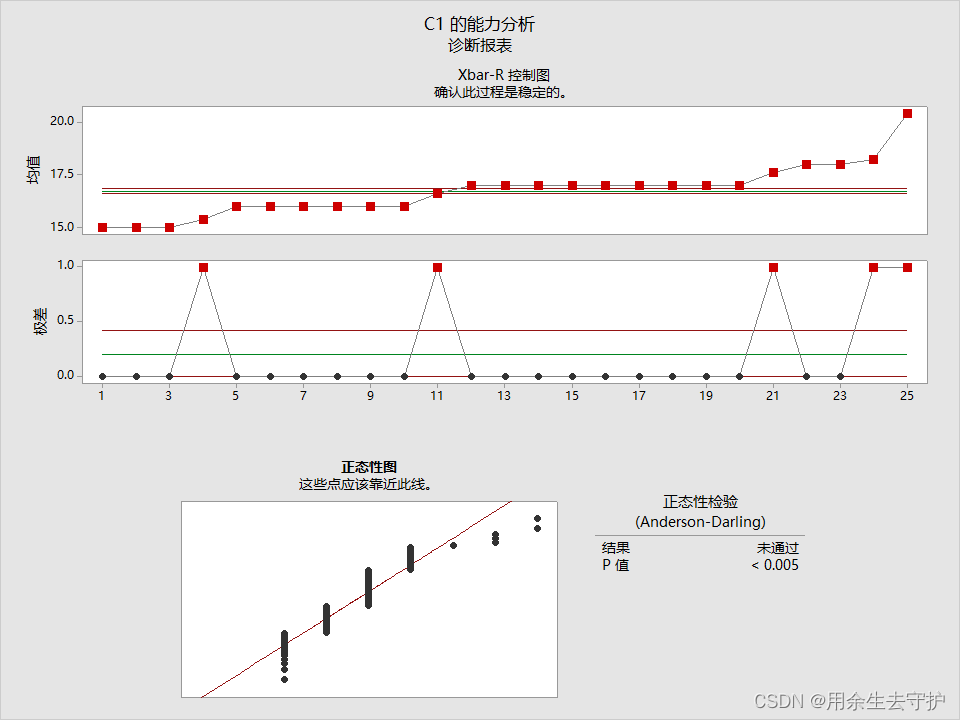





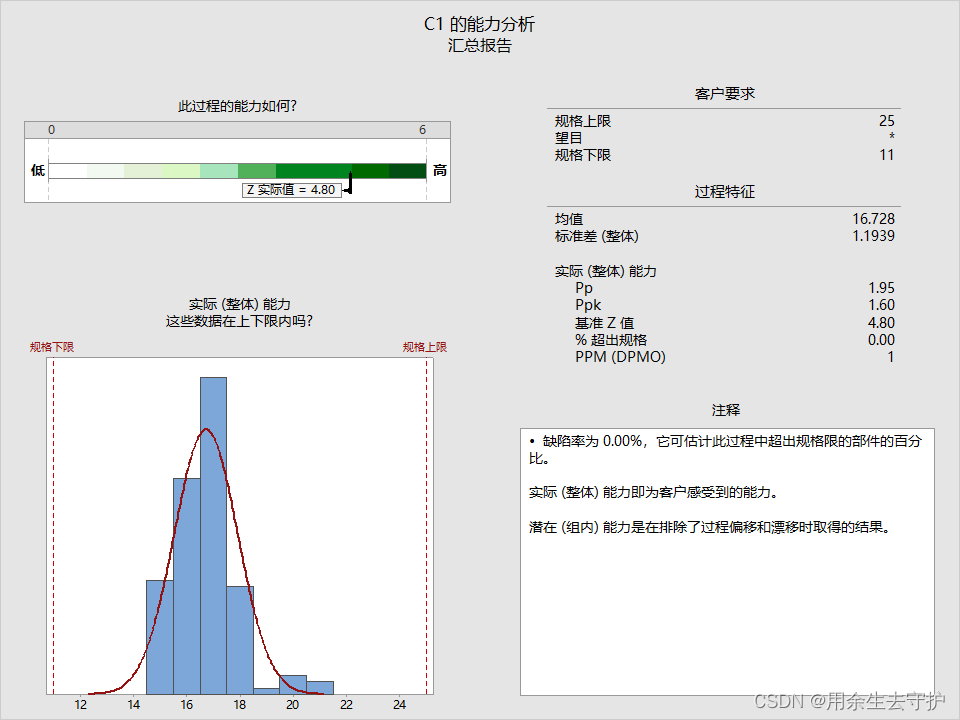
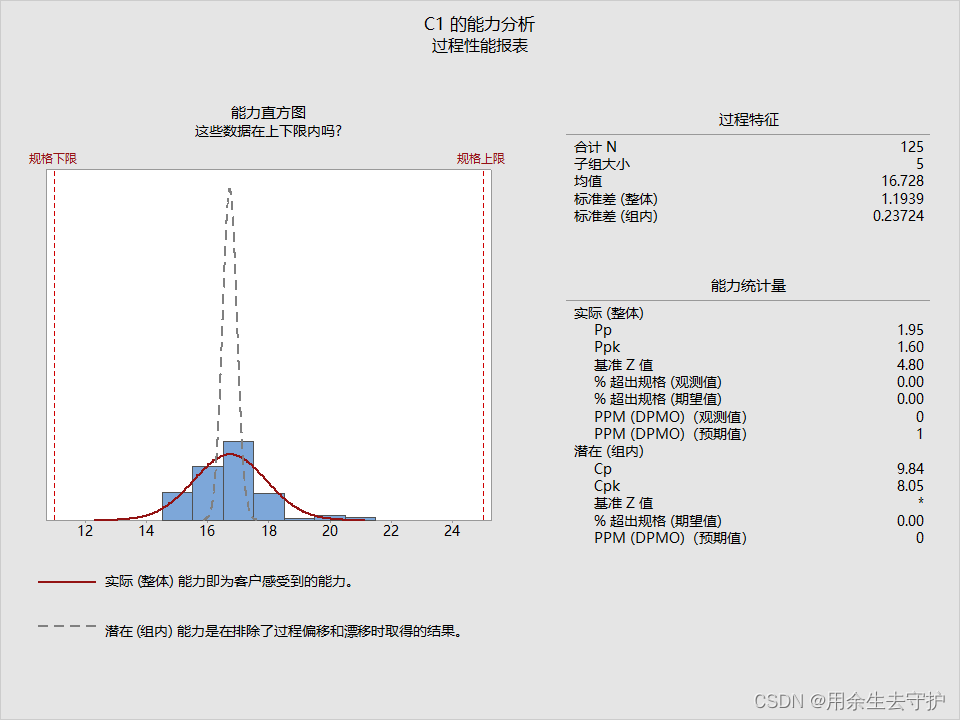
   可以看出排序后的CPK明显高于未排序，但是PPK值却是一样的，我们得出的结论是：排序后的过程能力要高于未排序的；

原因分析：

CPK=min｛（USL-μ）/3σ,（μ-LSL）/3σ｝

   PPK=min｛（USL-μ）/3S,（μ-LSL）/3S｝

   未排序：

排序后：

从公式中我们可以看出u，CPK与PPK的计算仅为标准差不一致，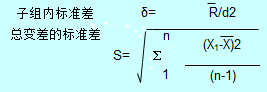

CPK中σ=子组内标准差（d2为常数，可查表得），而PPK中S=总变差的标准差，从公式可以看出σ受极差影响很大，而S并不会，我们可以看出，整体标准差（S）输出结果一样，而组内标准差（σ）排序后明显比未排序要小很多。

从此处也可以看出为什么CPK叫组内过程能力指数，而PPK叫整体能力指数。也可以看出CPK对过程取样的敏感性，计算CPK不仅要考虑三个前提，对数据的收集也有讲究，并不是任何情况下考虑CPK值都是有意义的。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删