产品
在大规模复杂系统的动力响应分析中，由于网格数目的急剧增加，自由度数目更是成倍数的增长，计算的时间成本也是成正比例上升的。通过超单元的设置，可以有效地将区块内的自由度数目缩减同时保证一定的计算精度。目前的简单例子的探索可以将计算时间缩短到原有时间的一半以上，对于长时间的计算是很有意义的。
下面这四张图是设置了整体架构的一部分作为超单元，保留了一部分的剩余结构计算得到的结果与全局计算得到的结果进行对比。选取了薄板上的四个不同位置的节点做出频响曲线。
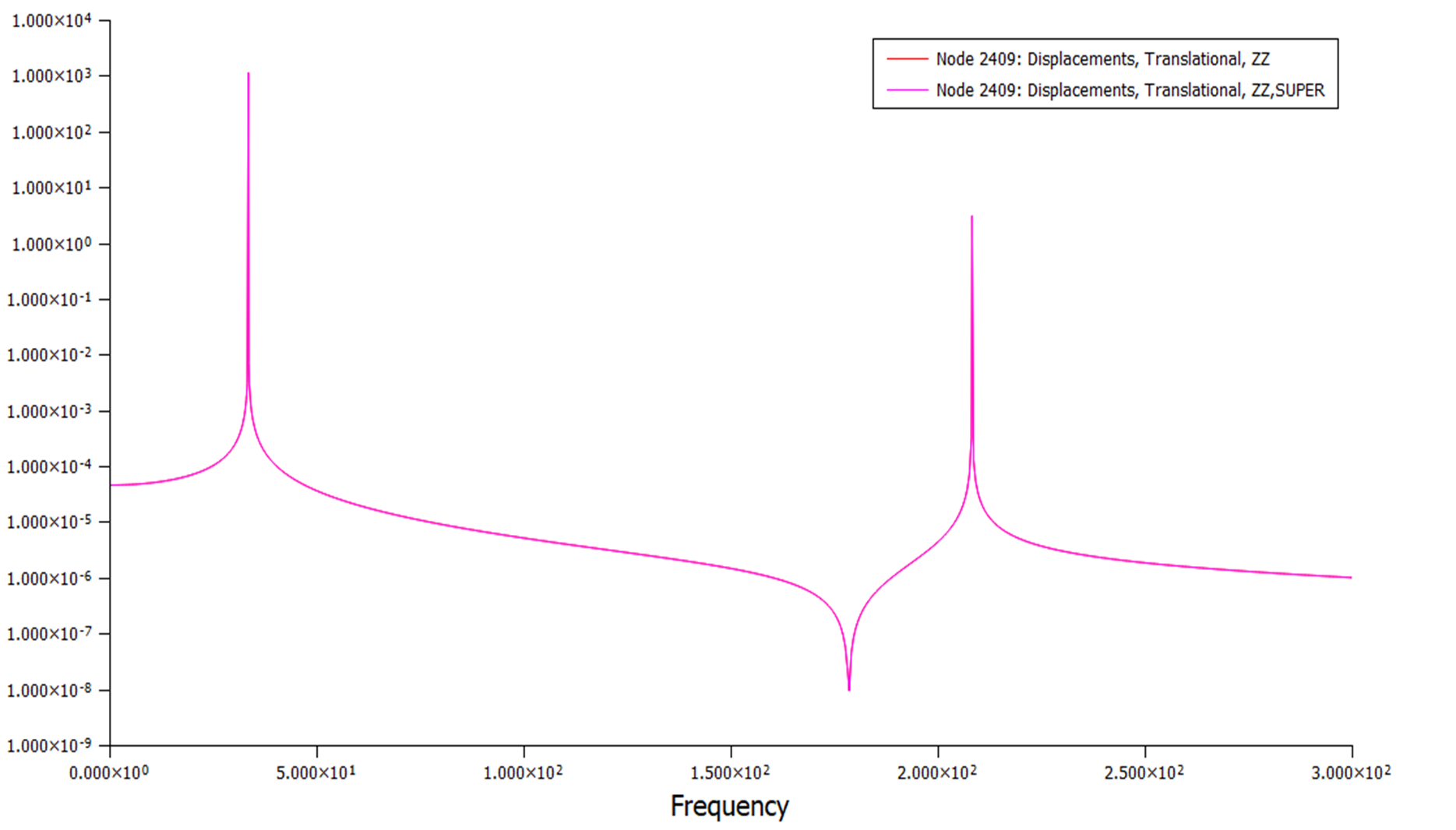
node2409两种不同计算方式的结果对比
node868两种计算方式结果对比
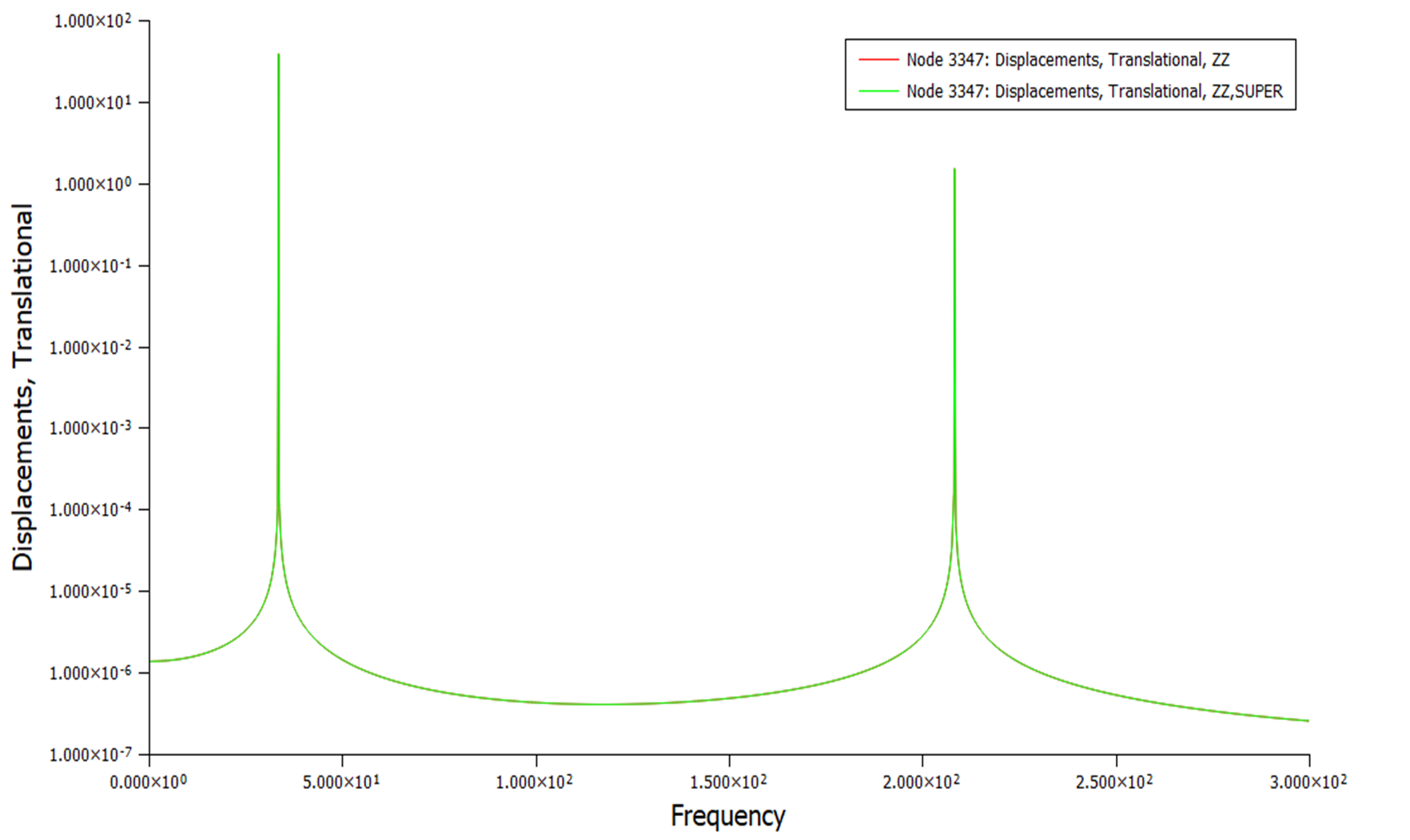
node3347两种计算方式结果对比
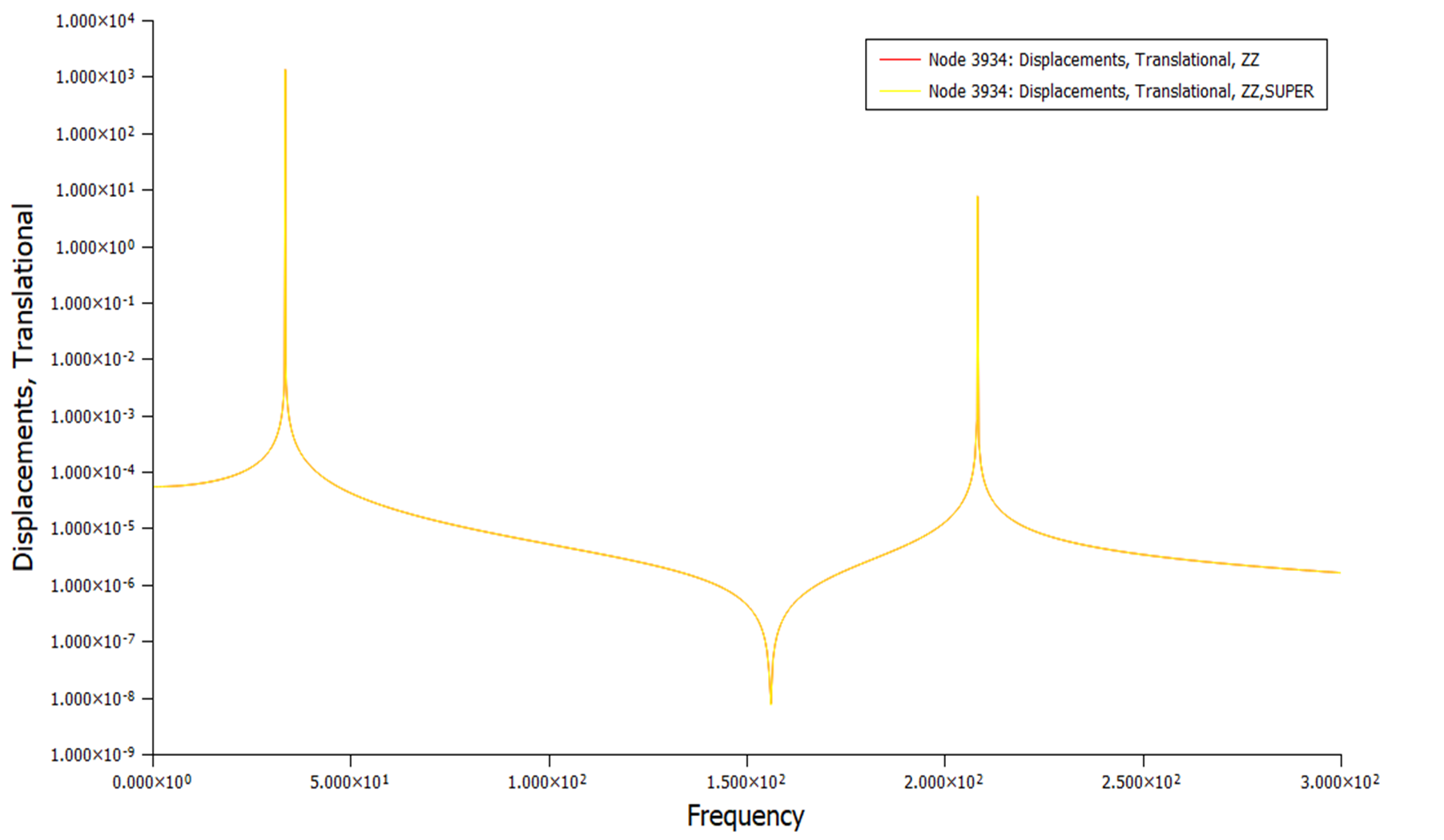
node3934两种计算方式结果对比
将两种计算方式得到的计算信息制表列出如下
部分超单元与全局计算得到的计算信息的统计
最完美的情况就是能够将所有的结构全部缩聚，得到一个比正常结构少几个数量级的自由度数目，下图是薄板分为两块超单元区域进行全部缩聚。
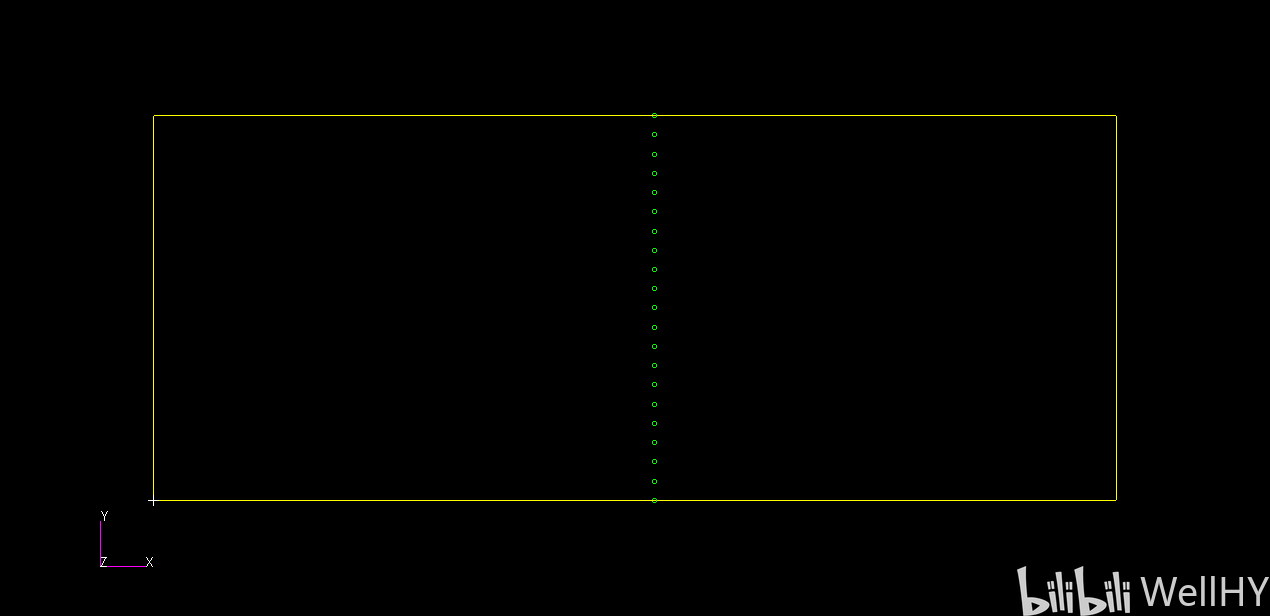
两块超单元区域划分
由于前面部分结构缩聚得到的结果图采用了两条实线，重叠情况严重，看不出有什么差异，故这次作图时采用一虚一实，更方便进行结果的观察。
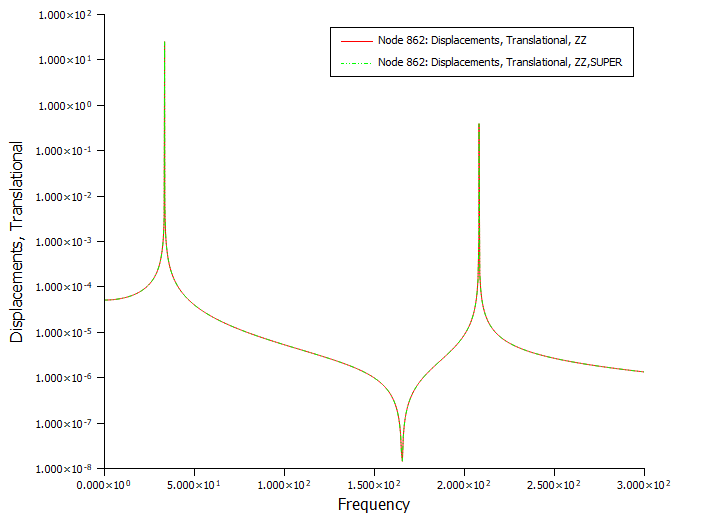
node862的结果对比
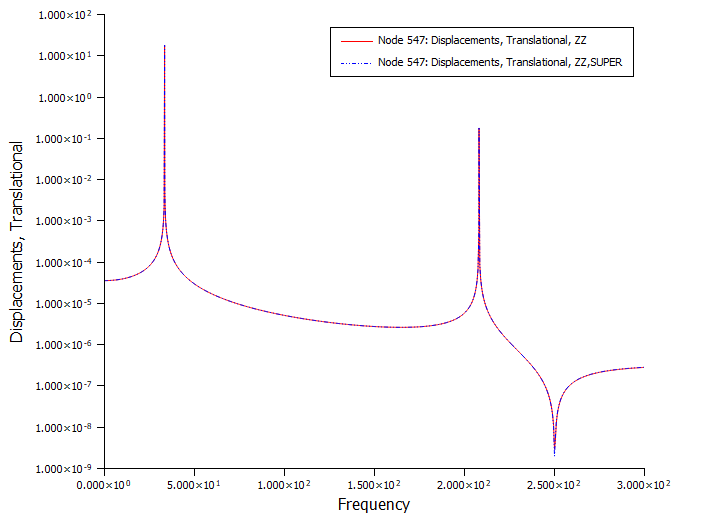
node547结果对比
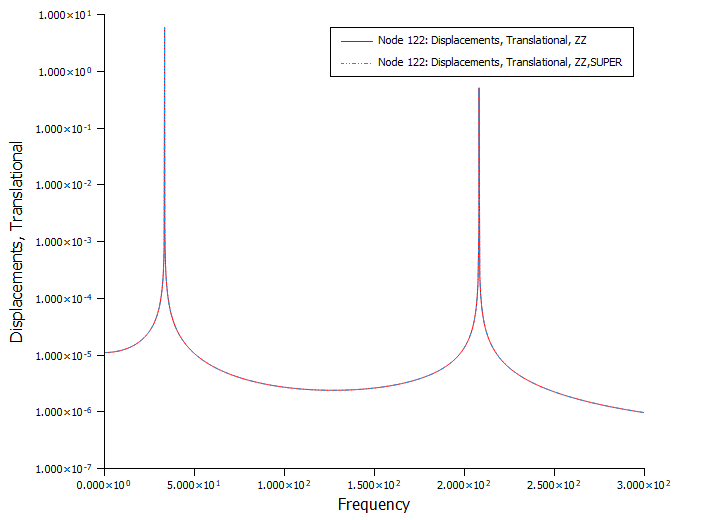
node122结果对比
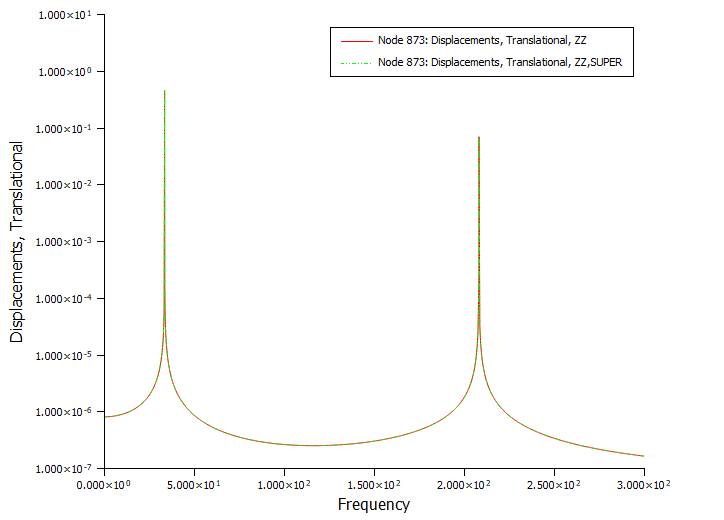
node873结果对比
将两种计算方式的计算信息进行统计列表如下：
全部结构缩聚与全局计算得到的计算信息
由此可以看出，结构缩聚的越彻底，得到的计算结果精度是有保证的，同时计算时间的大幅缩短可以带来不小的应用价值。
免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删
155-2731-8020
