1、 传递函数模型

首先将分子分母多项式用向量表示，然后利用MATLAB的控制系统工具箱中的tf函数建立传递函数模型，具体如下：

函数常用用法见下表：

表1.1 tf函数用法

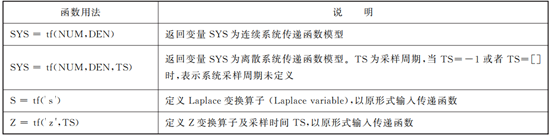
还有一些其他的相关函数如下：

表 1.2 MATLAB中构建传递函数相关函数

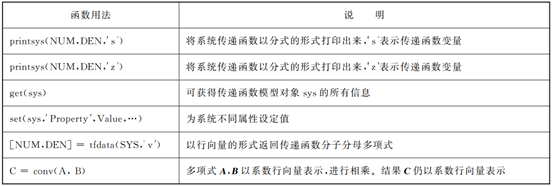
接下来举几个例子：

例1-1  利用MATLAB建立如下传递函数模型

（1）方法1

代码：

num=[2 1];     %分子多项式

den=[1 2 4 1];  %分母多项式

G=tf(num,den)

结果：

G =

        2 s + 1

 ---------------------

 s^3 + 2 s^2 + 4 s + 1

Continuous-time transfer function.

方法（2）

代码：

s=tf('s'); %先定义Laplace算子

G=(2*s+1)/(s^3+2*s^2+4*s+1)

结果：

G =

        2 s + 1

 ---------------------

 s^3 + 2 s^2 + 4 s + 1

Continuous-time transfer function.

2、 零极点模型

调用zpk(z,p,K)函数完成零极点函数模型的创建。

注意：当pamap函数有返回值时不在绘制零极点分布图

例1-1  试用MATLAB建立以下传递函数。

方法（1）

代码：

z1=[-5;-5];              %为零点赋值

p1=[-1;-2;-2-2*j;-2+2*j];  %为极点赋值

k=4;                    %为增益赋值

G1=zpk(z1,p1,k) %得到系统模型

结果：

G1 =

         4 (s+5)^2

 --------------------------

 (s+1) (s+2) (s^2 + 4s + 8)

Continuous-time zero/pole/gain model.

方法（2）

代码：

s=zpk('s'); %定义算子

G2=4*(s+5)^2/(s+1)/(s+2)/(s^2+4*s+8)

结果：

G2 =

         4 (s+5)^2

 --------------------------

 (s+1) (s+2) (s^2 + 4s + 8)

Continuous-time zero/pole/gain model.

方法2需要注意的是，对于共轭复数表示的零极点，需要展开成二阶多项式的形式。

3、 状态空间模型

（1）由A,B,C,D矩阵直接创建状态控制模型

sys=ss(A,B,C,D)

（2）对于离散的状态空间模型，需要设置采样时间Ts

sys=ss(A,B,C,D,Ts)

同样,也可以通过ssdata()函数来获得状态方程对象参数

[A,B,C,D]=ssdata(sys)     获得连续系统参数

[A,B,C,D,Ts]=ssdata(sys)   获得离散系统参数

例1-1  利用ss命令创建以下状态空间模型

代码：

A=[6 5 4;1 0 0;0 1 0]; %给状态矩阵A赋值

     B=[1 0 0];          %给输入矩阵B赋值

     C=[0 6 7];          %给输出矩阵C赋值

     D=[0];             %给前馈矩阵D赋值

     G=ss(A,B,C,D) %输入并显示系统状态空间模型

结果：

G =

 A =

      x1  x2  x3

  x1   6   5   4

  x2   1   0   0

  x3   0   1   0

 B =

      u1

  x1   1

  x2   0

  x3   0

 C =

      x1  x2  x3

  y1   0   6   7

 D =

      u1

  y1   0

Continuous-time state-space model.

4、 模型之间的转化

在实际的控制系统设计中，给出的模型跟我们需要的模型可能不是一种描述方式，所以MATLAB为我们提供了不同模型之间转换的函数。主要分为两大类，一类是将其他类型的模型转化成所需模型；另一种是将已有的模型转化成其他形式的模型。

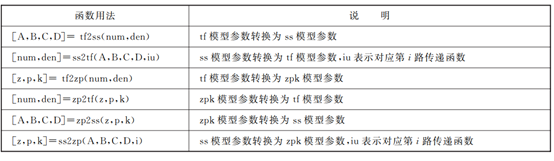
表 1.5 将其他类型的模型转化成所需模型

表1.6 将现有模型转化成其他类型的模型

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删