MATLAB数据可视化是极重要的功能,文章介绍了MATLAB绘图与数据可视化的相关方法,阅读本文读者可以快速掌握MATLAB绘图技巧,在"科研绘图模板"为读者提供了较为完善的三种绘图模板供读者尝试。
绘图的步骤:曲线数据准备(对于二维曲线准备横纵坐标数据,对于三维曲面准备矩阵参变量和对应的Z坐标值);指定图形窗口和子图位置(使用Figure命令指定图形窗口,默认时打开Figure1窗口,使用subplot命令指定当前子图);绘制图形;设置坐标轴和图形注释;对三维图形使用的着色和视点等设置;图形的精细修饰;按指定格式保存或导出图片。
基本绘图函数
plot(y) %绘制以y为纵坐标的二维曲线,y为矩阵时按列对y中数据绘图
plot(x,y)
plot(x1,y1,x2,y2,...) %同一窗口绘制多条二维曲线
多个图形的绘制
%% 同一个窗口多个子图
subplot(m,n,i) %将窗口分成(m*n)幅子图,第i幅为当前幅,编号原则:左上起先从左往右后从上往下
%% 双坐标图
plotyy(x1,y1,x2,y2) %以左、右不同的纵轴绘制两条曲线
%% 同一窗口多次叠绘
%一般调用plot函数都是绘制新图形而不保留旧有图形,使用hold命令可以保留原图形,使多个plot函数在一个坐标系中不断叠加
hold on %使当前坐标系和图形保留(仅保留数据和坐标轴属性)
hold off %使当前坐标系和图形不保留
hold %在上述两个命令间切换
hold all %使当前坐标系和图形保留,并且保留当前线的颜色和样式
%% 指定图形窗口
%使用plot等绘图命令时都是默认打开"Figure 1"窗口,使用figure则可以打开多个窗口
figure(n) %产生新图形窗口
设置图形样式
%% 曲线的线性、颜色和数据点型
plot(x,y,s) %s为字符串,用以设置曲线的线性、颜色和数据点型等。
plot(x,y,'mo-.') %绘制紫红色圆圈标记点划线
%% 设置坐标轴 坐标轴相关命令都是以axis开头
axis auto %使用默认设置
axis([xmin,xmax,ymin,ymax]) %设定坐标范围
axis equal %纵、横坐标采用等长刻度
%% 分割线和坐标框
%坐标框是指坐标系的刻度框 使用box on/box off/box控制
%分割线是指在坐标系中根据坐标轴刻度使用虚线进行分割
grid on %显示分割线 grid off %不显示分割线(默认设置) grid %在二者间切换
%% 图形注释
%图形注释包括设置标题(title)、坐标轴便签(label)、图例(legend)、添加标准元素(annotation)
%MATLAB支持部分tex公式,例如\alpha为自动识别为α
title('title'),legend('s1','s2',...,pos),xlabel('x'),ylabel('y');
test(xt,yt,'s') %在图形的(xt,yt)坐标处书写文字注释
annotation('type',[x1,x2],[y1,y2]) %根据type在指定坐标处添加注释元素,type: rectangle 为矩形,textbox 为文本框,line 为线,arrow 为箭头,textarrow 为带文字箭头,ellipse 为椭圆
线型 实线’-‘,双划线’–‘,虚线’:‘,点划线’-.’标记 实点. 圆圈o 叉号x 星号* 正方形s 菱形d 五角形p 六边形h 上下左右三角形^ v > <颜色 红r 绿g 蓝b 黄y 黑k 白w 青色c 紫红m
使用鼠标添加注释文字–当调节test(xt,yt,'s')位置不方便时可以使用
gtext('s') %用鼠标把字符串放在图形上
gtext({'s1','s2','s3'}) %一次将多个的字符串分行放置在图形上
gtext({'s1';'s2';'s3'}) %一次放置一个字符串分多次放置在图形上
%例如为正弦图形窗口添加文字标注
>> gtext({'\pi';'2\pi';'3\pi'})
使用鼠标获取图形数据
[x,y]=ginput(n) %用鼠标从图形上获取n个点的坐标(x,y)
特殊图形的绘制
bar(x,y,width,参数) %绘制横纵坐标、宽度分别为x,y,width的柱状图
area(x,y) %绘制横坐标为x,纵坐标为y的面积图;y可以是矩阵(多重面积图);若x省略则横坐标为1:size(y,1)
pie(x,explode,'label') %绘制各元素占总和的百分比
errorbar(X,Y,E) %绘制误差棒
quiver(x,y,u,v) %绘制以(x,y)为起点,横纵坐标为(u,v)的向量场
polar(theta,rho,参数) %绘制极坐标图
contour(z) %绘制矩阵z的等高线图
%% 绘制带误差棒的线条
x = linspace(0,10,15);
y = sin(x/2);
err = 0.3*ones(size(y));
errorbar(x,y,err,'-s','MarkerSize',10,...
'MarkerEdgeColor','red','MarkerFaceColor','red')
%% 科研绘图模板--二维
X=0:0.1:5;
Y=[sin(X); cos(X)];
%'MarkerIndices',1:1:length(y1)
plot(X,Y(1,:),'b.-',X,Y(2,:),'mo-.');
%绘图样式设置
title('Example 1');
xlabel('X'),ylabel('Y');
legend('s1','s2')
annotation('textarrow',[0.57,0.62],[0.5,0.5],'String','Y = sin(X)');
set(gca,'xtick',0:1:5); %设置刻度线密度
set(gca,'xminortick','on');%小刻度打开
set(gca,'ticklength',[0.025 0.0125]);%设置刻度线长度(大刻度与小刻度长度)
set(gca,'ytick',-1:0.5:1); %设置刻度线密度
set(gca,'yminortick','on');%小刻度打开
set(gca,'ticklength',[0.025 0.0125]);%设置刻度线长度(大刻度与小刻度长度)
box off
ax2 = axes('Position',get(gca,'Position'),...
'XAxisLocation','top',...
'YAxisLocation','right',...
'Color','none',...
'XColor','k','YColor','k');
set(ax2,'YTick', []);
set(ax2,'XTick', []);
box on
%% Example 2
figure %新建图表
x = 0:0.1:1;
y = [2./(x+1); x; x.^2; x.^4];
plot(x,y(1,:),'r.-');
hold on;
plot(x,y(2,:),'m*--');
plot(x,y(3,:),'bo:');
plot(x,y(4,:),'k^-.');
title('Example 2')
grid on;
set(gca,'FontSize',10); %横纵轴标注字体大小;
set(gca,'xtick',0:0.1:1); %设置刻度线密度
set(gca,'ytick',0:0.3:2);
xlabel('x','FontSize',15);
ylabel('y','FontSize',15);
text(0.5,0.5,'o [0.5,0.5]');
legend('2/(x+1)','x','x^2','x^4');
%% subplot
figure
t=0:0.01:2*pi;
for k = 1:9
y=sin(k*t);subplot(3,3,k);plot(t,y);title(['sin(',num2str(k),'*t)'])
end
suptitle('Example 3');
%% 保存文件
savename = ['sphere1']; % 设置输出文件名
Figure_num = 1; %获取第i张图'Figure i',也直接用gcf获取当前窗口句柄 Figure_num=gcf
print(Figure_num,[savename,'.png'],'-r600','-dtiff'); % 设置保存格式及分辨率,
假设此时我们有excel形式的实验数据需要对其进行处理,数据节选如下
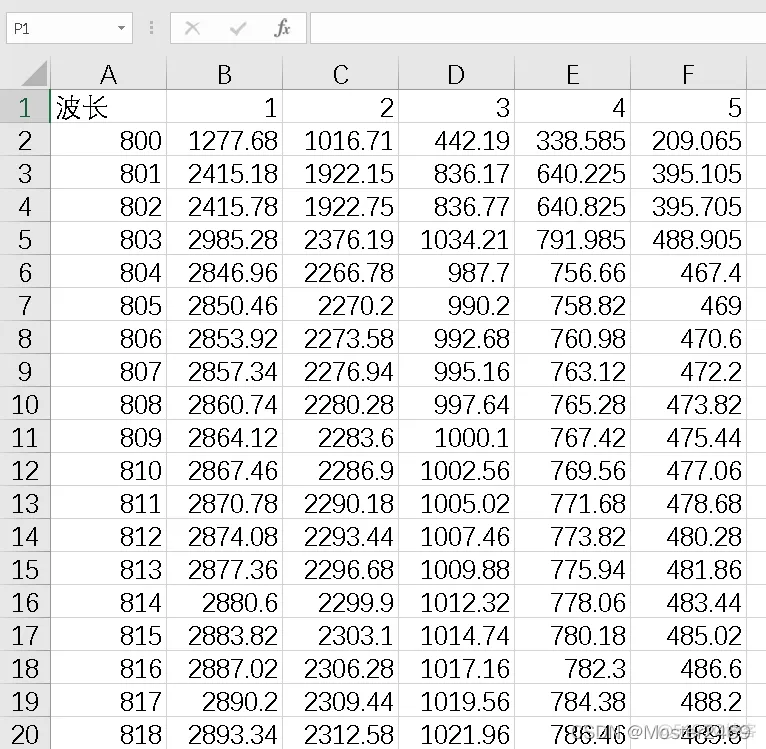
那么我们再配合MATLAB打开Excel的知识就可以直接利用Excel中的数据作图,代码如下
clc;clear all;close all;
figure %新建图表
[num]=xlsread('D:\FilePath\example.xlsx') ;
x = num(2:end,1);
y = num(2:end,[2:end]);
len_y = length(y(:,1));
plot(x,y(:,1),'r.-','MarkerIndices',1:50:len_y);
hold on;
plot(x,y(:,2),'m*--','MarkerIndices',1:50:len_y);
plot(x,y(:,3),'bo:','MarkerIndices',1:50:len_y);
plot(x,y(:,4),'k^-.','MarkerIndices',1:50:len_y);
plot(x,y(:,5),'r-p','MarkerIndices',1:50:len_y);
grid on;
xlabel('lambda (nm)','FontSize',15);
ylabel('E_{\lambda T} (W/m^3)','FontSize',15);
set(gca,'FontSize',10); %横纵轴标注字体大小;
set(gca,'xtick',800:300:3600); %设置刻度线密度
set(gca,'ytick',-500:500:4000);
text(0.5,0.5,'o [0.5,0.5]');
title('黑体辐射');
legend('2999k','2889k','2548k','2455k','2303k')
savename = ['figure']; % 设置输出文件名
Figure_num = 1; %获取第i张图'Figure i',也直接用gcf获取当前窗口句柄 Figure_num=gcf
print(Figure_num,[savename,'.png'],'-r600','-dtiff'); % 设置保存格式及分辨率
处理结果如下
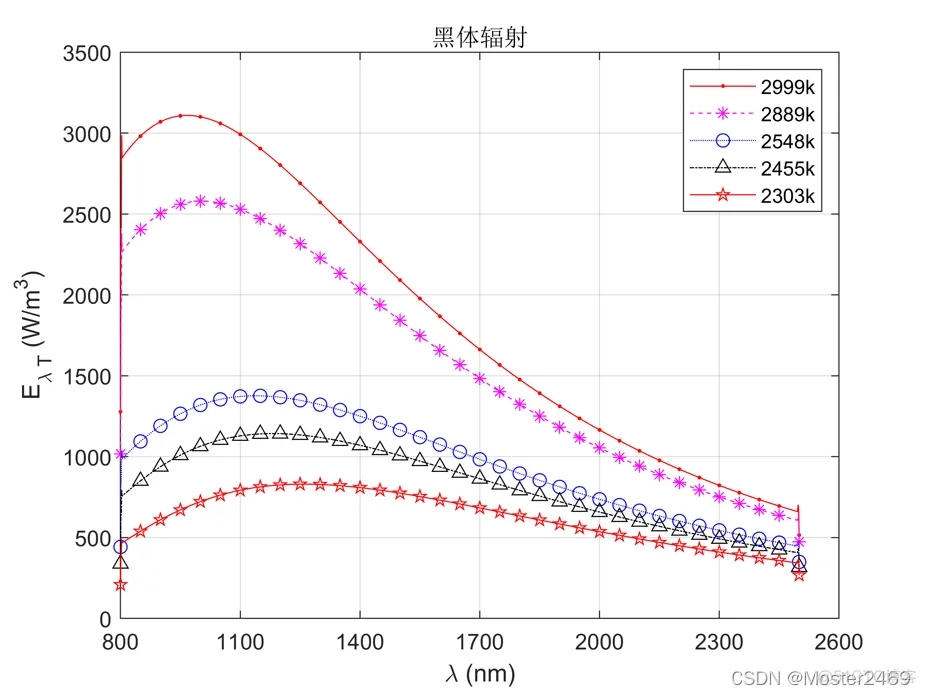
熟练使用MATLAB对Excel中的数据进行提取并绘图可以更好的进行数据可视化。
PS:笔者没有调节细节可能有些粗糙,大家可以根据自己的喜好进行调整。
Tips:MATLAB中支持latex格式的行内公式,例如要输入
MATLAB绘制的三维图形包括三维曲线、三维网格和三维表面图。三维图形与二维图形相比需要的数据是三维的,并且还增加了颜色表、光照、视角等设置。
三维曲线图
plot3(x,y,z) %绘制三维曲线
>> x=[0:0.2:10;30:0.2:40]; %两列数据
>> y=sin(x)
>> z=cos(x)
>> plot3(x,y,z)
三维曲面图
%% 三维曲面函数
mesh--三维网线图; meshc--三维网线图(带等高线版); meshz--三维网线图(带围裙线版);
surf--三维表面图; surfc--三维表面图(带等高线版);
waterfalll--三维瀑布图; ribbon--三维彩带图,只显示一维数据;
Contour3--三维等高线图; surf1--三维表面加光照效果
绘图步骤
%1.产生矩形网络
x=1:5;y=1:3;
[X,Y]=meshgrid(x,y) %产生XY矩形网络
%2.三维网线图
x=0:10; [X,Y]=meshgrid(x) %y省略则表示x=y
Z=X.^2+Y.^2;
mesh(X,Y,Z) %(X,Y)是通过meshgrid得到的网格顶点,C是指定各点颜色的用色矩阵mesh(X,Y,Z,C),省略时用色矩阵默认为Z
%3.三维网面图
surf(X,Y,Z,C)
设置视角
三维图形在不同的位置观察会有不同的结果,因此需要设置视角。视角是由方位角和俯仰角决定的,与x平面所成的夹角称为方位角(Azimuth), 与z平面所形成的夹角称为俯仰角(Elevation)。
view([az,el]) %通过方位角和俯仰角设置视角
view([x,y,z]) %通过(x,y,z)直角坐标设置视角
例:改变视角观察
x=-8:0.6:8;
[X,Y]=meshgrid(x);
Z=sin(sqrt(X.^2+Y.^2))./sqrt(x.^2+Y.^2);
subplot(2,2,1)
surf(X,Y,Z)
subplot(2,2,2)
surf(X,Y,Z)
view(2) %二维平面
subplot(2,2,3)
surf(X,Y,Z)
view([180,0]) %侧面图
subplot(2,2,4)
surf(X,Y,Z)
view([1,1,5]) %根据向量[1,1,5]的方向设置视角
设置色彩
MATLAB使用色图作为着色的基础,色图是一个的矩阵,m的值通常是64,代表真正用到的颜色个数。
默认的色图为hsv,gray代表灰度对照表,spring代表春天色对照表。
x=-8:0.6:8;
[X,Y]=meshgrid(x);
Z=sin(sqrt(X.^2+Y.^2))./(sqrt(X.^2+Y.^2));
colormap(spring) %设置色图
surf(X,Y,Z)
colorbar %显示颜色表
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删