MATLAB中的关系运算符有以下六个:
关系运算符可以用来比较两个数组中元素的关系,如果比较的结果为真,则MATLAB会返回逻辑值1;如果结果为假,则会返回逻辑值0。这里的逻辑值1和0实际上就是其他编程语言(例如C语言、Java等)中的布尔型(bool)变量,布尔型变量的值只有真(true)和假(false)。逻辑值1和逻辑值0可以简称为逻辑1和逻辑0,对应的英文为logical 1和logical 0。
下面我们举一个例子,大家可以观察MATLAB的返回结果:

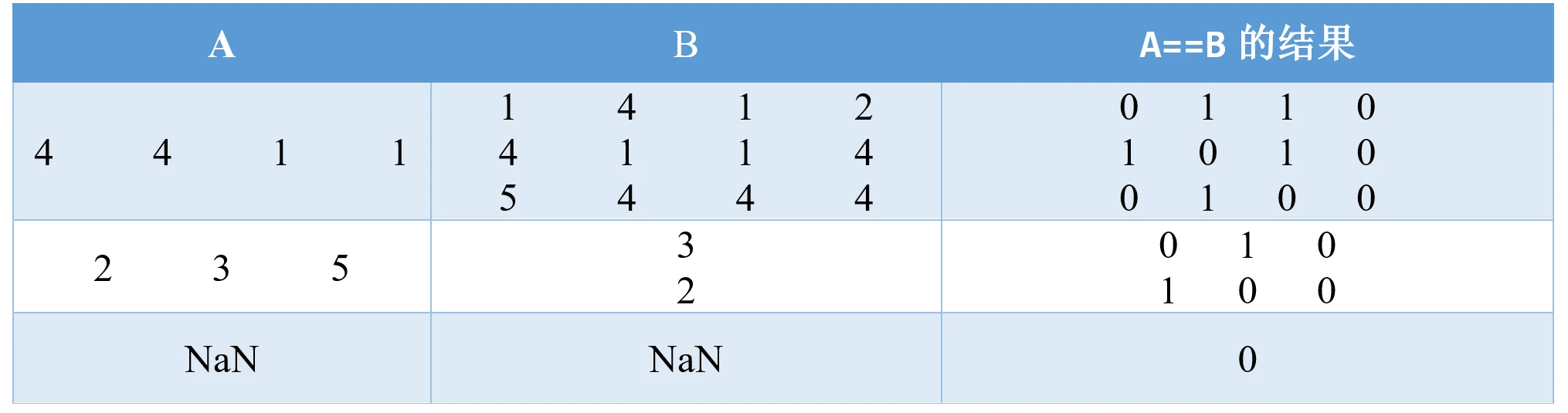
注意:(1)上面表格第三列的0和1实际上是逻辑值0和逻辑值1;(2)NaN(不定值或缺失值)相互之间不相等。
易错点:连续使用关系运算符:有许多初学者喜欢连续使用多个关系运算符,大家可以试试下面四条命令,观察MATLAB返回的结果是什么:
(1)0 == 0 == 0
(2)1 == 1 == 1
(3)-1 < 0 < 1
(4)1 > 0 > -1
在MATLAB中,连续使用多个关系运算符可能会产生意想不到的结果,上面四条命令的返回结果如下:

这些不符合预期的结果源于MATLAB对多个连续关系运算符的解析方式。以第一条命令为例:0 == 0 == 0 实际上被解析为 (0 == 0) == 0。由于 0 == 0 为真(logical 1),因此最终的表达式变为 1 == 0,结果为假(logical 0);第三条命令也是类似的,-1 < 0 < 1实际上被解析为 (-1 < 0) < 1。由于 -1 < 0为真(logical 1),因此最终的表达式变为 1<1,结果为假(logical 0)。第二条和第四条命令也是类似的解释。
因此,为了避免不必要的错误,我们应该使用下一小节中介绍的逻辑运算函数(逻辑与&、逻辑或|、逻辑非~等)连接多个关系表达式,例如判断a<b<c对应的命令应为(a<b)&(b<c),这里的&表示逻辑与,只有当a<b和b<c同时成立时才返回逻辑值1,下一小节会详细介绍。
另外,从上面的例子可以看出,逻辑值1和逻辑值0不仅仅用于表示真true和假false,它们在进行计算时也可以被视为数值1和数值0。
请看下面的例子:
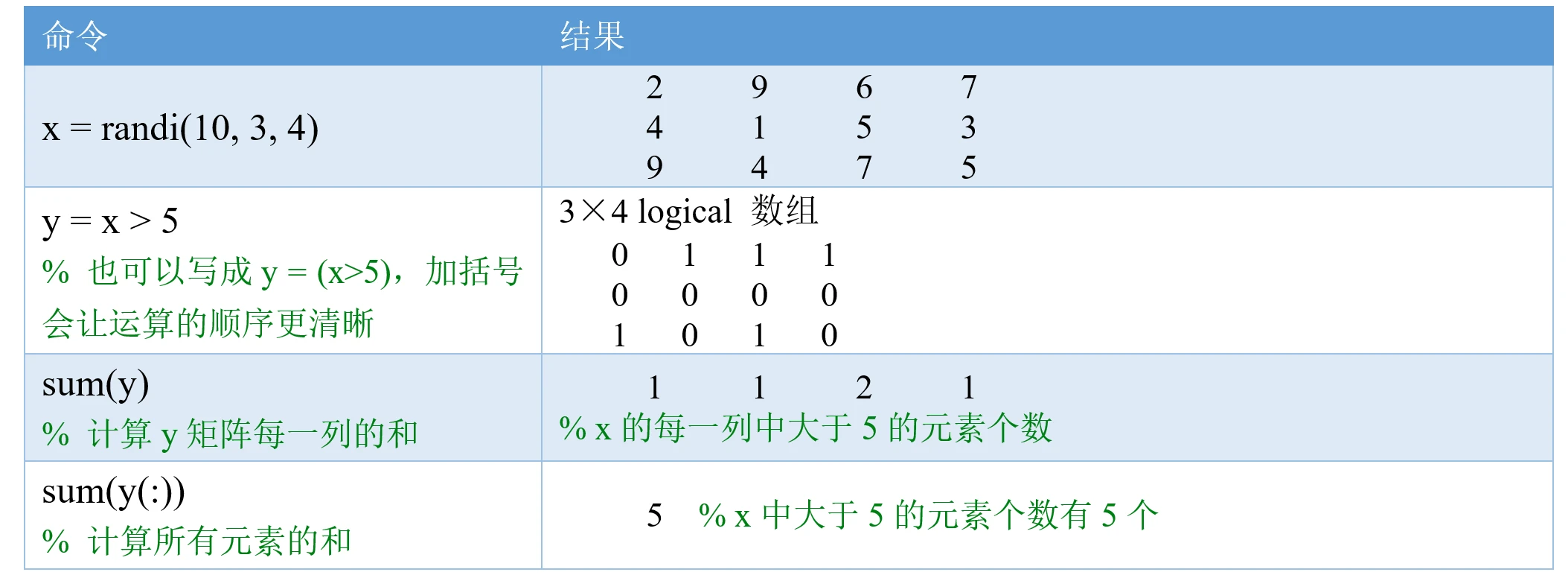
再来看一个例子:模拟投硬币10万次,计算出现正面的次数和频率。

下面我们再来看一个易错点:判断浮点数是否相等
先给大家简单介绍下什么是浮点数,浮点数是计算机科学中用于近似表示实数的一种数值表示法。简单来说,浮点数由两部分组成:一个表示数字的部分(称为尾数)和一个表示数字所在位置的指数。例如,数字1234.56可以写成,其中1.23456是尾数,3是指数。
有编程基础的同学应该知道,计算机中的数据是使用二进制0和1来保存的,例如十进制表示的3在二进制中表示为11。虽然十进制能精确表示如0.1这样的数,但在二进制中,0.1却需要表示为一个无限循环的小数0.00011001100110011…。由于计算机的内存是有限的,这导致了它无法精确表示0.1这样的数值。计算机在处理这类数字时会进行截断或舍入,所以使用浮点数计算时可能会产生误差。
MATLAB中的浮点数分为两种,分别是双精度(double)浮点数和单精度(single)浮点数,两种浮点数能表示的数值的范围有所不同。默认情况下我们创建的向量或者矩阵中的元素都是使用双精度浮点数表示的,对这部分内容感兴趣的同学可点击下方链接,MATLAB的官网有详细介绍两种的区别:https://ww2.mathworks.cn/help/matlab/matlab_prog/floating-point-numbers.html。
大家可以尝试计算 0.5-0.4-0.1,这是我的MATLAB返回的结果:

理论上C应该等于0,但由于浮点数计算的误差,MATLAB得到的C约为-2.7756×10-17,这是一个非常接近0的数。当我们试图判断C是否等于0时,MATLAB返回逻辑0,即MATLAB认为C不等于0,这显然不是我们期望的结果。
那么我们应该怎样判断两个浮点数相等呢?
解决方法:使用一个很小的正数来比较浮点数,而不是直接使用双等号(==)判断。我们将这个很小的正数称为容差(tolerance,简称为tol),例如要比较A和B两个数是否相等,只需要满足: ,这里的容差tol通常取一个非常小的正数,例如tol可取成1e-12(10的-12次方)。tol越小,判断两个浮点数相等的要求越严格。

当然,并非MATLAB中所有的浮点数计算都会出现误差。例如,如果我们仅交换0.1和0.4的位置:

总之,当我们需要判断两个浮点数是否相等时,务必要考虑到计算的误差。感兴趣的同学可以进一步搜索和学习有关浮点数的知识。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删