Abaqus中常用零件类型的详细介绍

来源：复合材料力学

作者：君莫

Abaqus中创建零件时一般有Deformable、Discrete rigid、Analytical rigid、Eulerian四种类型。下面分别介绍一下：

可变形体是有限元分析中采用的最多的一类零件，指物体在载荷（机械载荷、热载荷、电载荷等）作用下可产生变形，适用于任意二维或三维几何。

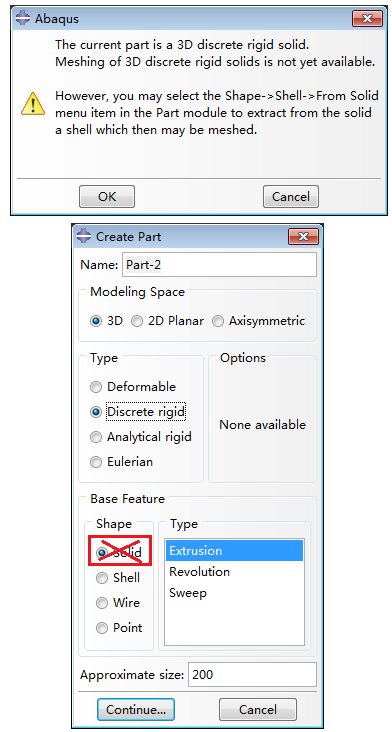
（2）Discrete rigid离散刚体

离散刚体，顾名思义这是一种刚体，一般用于模拟不可变形体接触分析。其几何与可变形体类似，可以是任意形状。

采用离散刚体形式建立的零件，可以是任意形状的二维、三维及轴对称结构。但是只有包含壳或者线框的离散刚体零件才能够划分网格，实体零件无法划分。如果采用实体几何，属性选择离散刚体，划分网格时会提示将几何转化为壳体。

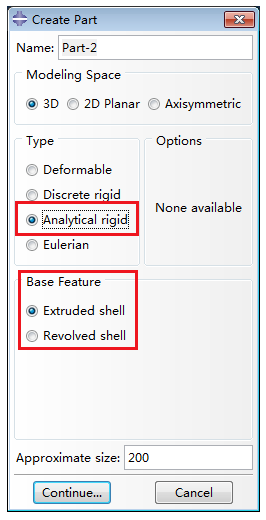
（3）Analytical rigid分析刚体

分析刚体与离散刚体类似，在接触分析中采用的是刚性面，分析刚体并非适用于任意几何形状，其几何必须是由一系列草图曲线、弧线和抛物线通过拉伸、旋转而成的平面或曲面。

分析刚体零件相比离散刚体零件而言，计算量较小，但是不能是任意形状，其轮廓必须光顺。

刚体是指在运动中和受力作用后，形状和大小不变，而且内部各点的相对位置不变的物体。绝对刚体实际上是不存在的，只是一种理想模型，因为任何物体在受力作用后，都或多或少地变形，如果变形的程度相对于物体本身几何尺寸来说极为微小，在研究物体运动时变形就可以忽略不计。

（4）Eulerian欧拉体

欧拉体一般用于模拟液体，气体或者大变形体。材料可以在欧拉域中流动，但网格自身在分析过程中不会变形，取而代之的是，零件内的材料物质在外载荷作用下发生变形，

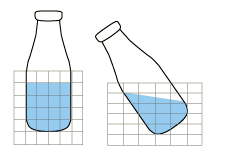
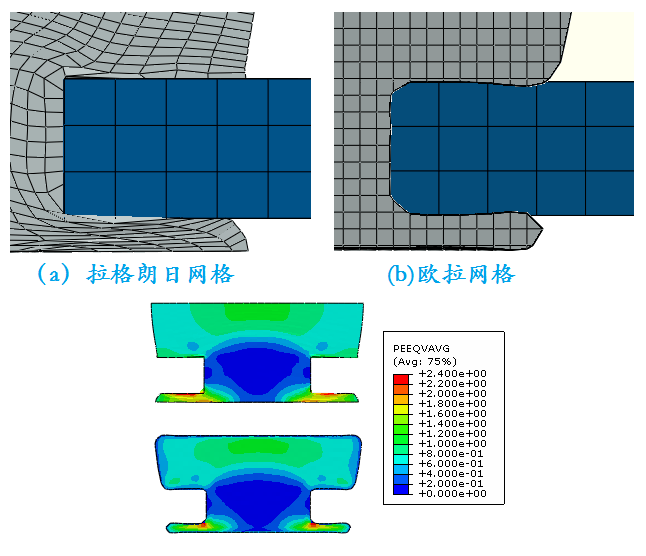
比如铆钉成型过程、冲压过程等零件可以用欧拉体，对应的是网格在空间中的位置不变，物质在网格中流动。大变形分析中，采用欧拉网格可以避免传统拉格朗日网格分析时的单元畸变问题，在金属塑性成型分析中应用广泛。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删