小球在弹簧顶端木块上弹性跳动问题代码分析

小球在弹簧顶端的木块上的弹性跳动问题之代码分析

根据上次课程的原理分析及给出的代码（http://www.jishulink.com/content/post/318856），这次课程的任务是对给出的代码进行分析。本次课程分为三部分，一是上一节课程中的结果展示，二是代码实现分析；三是代码分析。

我们先按照给出的代码运行程序，得出了以下图片。

1.结果展示

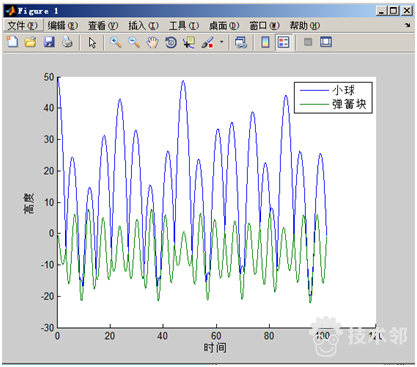
图 1.小球与弹簧块位移图

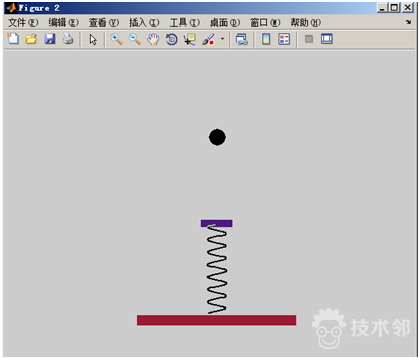
图 2.小球与弹簧块运动动画（动图）

得到了小球与弹簧块的位移图（图1）与小球与弹簧块运动（图2），在图1中看到小球与弹簧块接触25次，这个数值是在代码中设定的；图2是一张动画图，展示的是小球与弹簧块的运动过程。

2.代码实现分析

从上一节课程中我们了解到，小球与弹簧块的运动过程分为两大部分，一是未碰撞情况下，我们运用基本的受力分析以及位移，速度，加速度的关系可得方程；二是碰撞的情况下，我们采用动量守恒定律以及能量守恒定律得到方程。代码运行应该符合下列流程图。

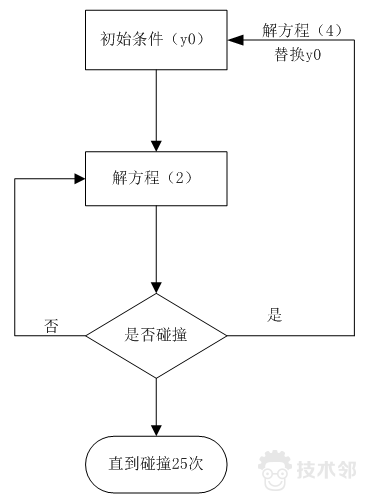
图3 代码实现流程

首先根据给定的初值，进入方程组（2），直到小球与弹簧块碰撞时进入方程组（4），如此便得到了小球与弹簧块第一次碰撞间的所有过程，因为本例不存在任何阻尼的作用，所以，小球将弹起，弹簧块将下降，从新进入到方程组（2），再开始一个新的循环。理论上来讲，这将是一个无限的循环，但我们可以通过设置小球与弹簧块的碰撞次数来限定，在代码中，设定的25次。

3.代码分析

3.1 解微分方程基本知识

微分方程分为常微分方程（ODE）与偏微分方程（PDE），简单来说系数为常数的为ODE，而系数为变量的为PDE。目前Matlab提供了多种解微分方程的结算器，如ode113、ode15i、ode23s、ode3t等，以后有机会将系统的阐述各种算法的差异以及其各种擅长的领域，现在只需要记住，一般默认ode45算法即可，Matlab公司的建议是，如果不清楚系统的具体情况，建议先选择ode45。常微分解法器的输入输出格式有：

[t,Y] = solver(odefun,tspan,y0)；

[t,Y] = solver(odefun,tspan,y0,options)；

[t,Y,TE,YE,IE] = solver(odefun,tspan,y0,options)；

上述指令的“solver”所指的就是ode45、ode45, ode23, ode113, ode15s, ode23s, ode23t, or ode23tb等，其他参数的含义介绍如下：

a) odefun 用以计算微分程右边的函数，所有解法器处理的系统方程形式均是y’=dydt=f(t,y)的形式，通常可由odefile模板改写而成；

b) tspan 为积分区间的向量[t0,tf],解法器设定初值在tspan(1)，然后由tspan(1)积分至tspan(end)。如果需要得到特定时间所对应的解，可以用tspan[t0,t1,…,tf]的形式。使用tspan向量的大小并不影响运算的时间，影响的是存储的空间；

c) y0 为初始向量指；

d) options 为改变积分特性的参数，可以用odeset设定，如本先将积分器中的时间判定功能打开；

e) [t Y] 为输出值，t是时间点的行向量，Y是解答列阵，每一行Y均与时间t所对应，每组(t,Y)所产生称为事件函数，每次均要检查是都等于0，并决定在零指时是否终止运算；

3.2 “events”函数分析

基本形式为：[value, isterminal,direction]=events(t,y)

其中value(i) 为函数的值，isterminal(i)=1时运算在等于0时停止，isterminal(i) =1时运算在等于0时继续；direction(i)=1在事件函数增加时等于零，direction(i)=-1在事件函数减小时等于零。这一功能与上一小节“e）”点组合理解。

3.3 代码分析

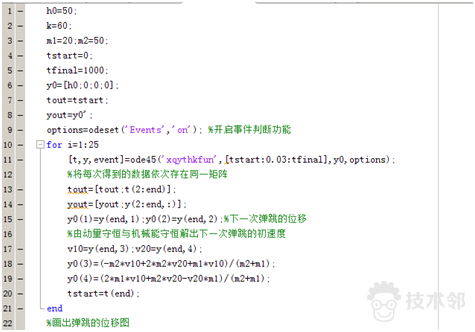
图4.代码分析1

这一部分主要实现的是解微分方程，可以说是整个算法的全部。首先设定小球下落高度为50，弹簧系数为60；小球质量为20；弹簧块质量为50；积分开始时间为0，结束时间为1000，注意这不是系统时间，1000也不是意味着1000秒，而是用于微分解算器中tspan参数设定；初值为[h0,0,0,0]，其中h0是小球初始高度，第二个“0”指的是弹簧块的初始位置（坐标原点，为0），第三个0指的是小球的初始速度，为0意味着是静止下降，第四个0指的是弹簧块的初始速度。