/*仅当作学习笔记,若有纰漏欢迎友好交流指正,此外若能提供一点帮助将会十分荣幸*/
在前面两篇博文中我们分别介绍了病毒模型的基本计算思路方法以及基本再生数R0,这里我们将会简单的列举几种经典的病毒动力学模型的动力学逻辑、微分方程及迭代仿真。
摘 要:本文将介绍SIR、SEIR、、SIVRS病毒模型并补充SEIH谣言传播模型,并通过MATLAB仿真出动力学微分方程。
SIR
SIR病毒模型作为传染病研究中最经典的动力学模型,作为很多病毒模型研究的基础。其中S表示易感染者,I表示感染者、R表示移除者,起动力学逻辑如图所示:

其微分方程为:
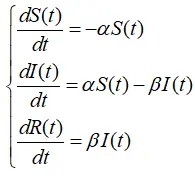
其中α代表感染率、β代表移除率。
Matlab代码:--------------------------
clear;clc;
%各种状态人群参数设置
N = 1;%人口总数
I = 0.2;%感染者
S= N-I;%易感者
R=0;%免疫者
%模型系数设置
b=0.5;%感染系数
c=0.25;%康复系数(感染者转会免疫者系数)
T= 0:20;%迭代总时长
for idx = 1:length(T)-1
S(idx+1) = S(idx)-b*S(idx);%易感者S迭代
I(idx+1) = I(idx)+b*S(idx)-c*I(idx);%感染者I迭代
R(idx+1) = c*I(idx);%免疫者R迭代
end
figure
plot(T,S,T,I,T,R);
grid on;
xlabel('天');ylabel('人数')
legend('易感者S','感染者I','免疫者R')
title('SIR')

----------------------------------------------------
仿真图:
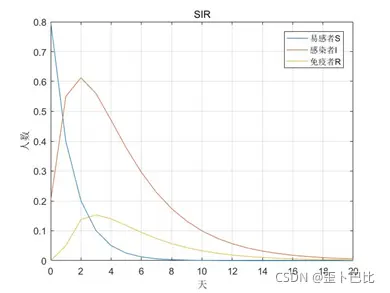
SEIR
SEIR模型是以SIR模型为基础加入潜伏节点E(t),表示在t时刻潜伏者在络中的比例。易感者S中部分以概率λ直接被感染成为感染者I,另一部分以α的感染率变成潜伏者E,潜伏者E以β的概率转化为感染者I,感染者I则以λ的免疫率被治愈获得抗体且不会被再次感染也不会改变状态成为免疫态R,其动力学逻辑如下所示:
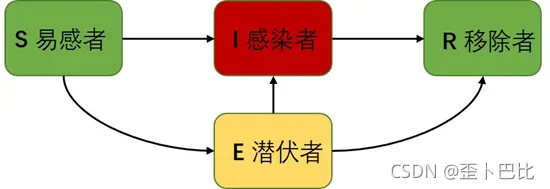
其传播动力学微分方程为:
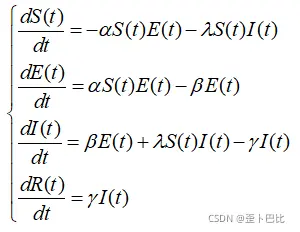
Matlab代码:------------------------------
clear;clc;
%各种状态人群参数设置
N = 1;%人口总数
I = 0.2;%感染者
S= N-I;%易感者
R=0;%免疫者
E=0;%潜伏者
%模型系数设置
a=0.2;%转为潜伏者系数
b=0.6;%感染系数
c=0.8;%康复系数(感染者转会免疫者系数)
d=0.2;%潜伏者染病系数(潜伏者转为感染者系数)
T= 0:20;%迭代总时长
for idx = 1:length(T)-1
S(idx+1) = S(idx)-a*S(idx)*E(idx)-b*S(idx)*I(idx);%易感者S迭代
E(idx+1) = E(idx)+a*S(idx)*E(idx)-d*E(idx);%潜伏者E迭代
I(idx+1) = I(idx)+d*E(idx)+b*S(idx)*I(idx)-c*I(idx);%感染者I迭代
R(idx+1) = a*I(idx)+c*I(idx);%免疫者R迭代
end
figure
plot(T,S,T,E,T,I,T,R);
grid on;
xlabel('天');ylabel('人数')
legend('易感者S','潜伏者','感染者I','免疫者R')
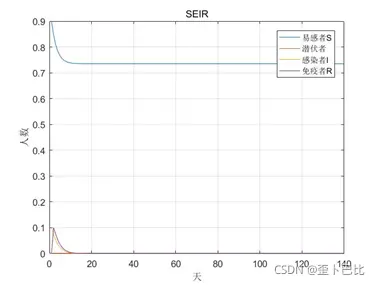
title('SEIR')
----------------------------------------------
仿真结果:
SIVRS
在SEIR模型的基础上,同时还考虑到变异的存在,并且假设系统存在于一个封闭的复杂网络中,有学者就提出了SIVRS模型。假设N为种类常数,δ表示为初始出生率,网络平均度为<k> ,易感者S接触感染者I后感染概率为α,当感染者接触变异者之后变异率为γ,同时感染者以内部概率η变异为V,部分感染者以β概率恢复为免疫者R, 另外一部分感染者则一直保持感染态,免疫者(移除者)R以一定概率恢复为S,四个种群均有相同的死亡率μ。
该模型特点:
①考虑到出生率(即模型总量的变化)
②考虑到病毒的变异
③考虑到免疫者变回为易感者
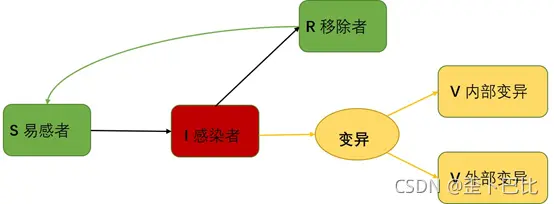
其动力学逻辑如下所示:
其传播动力学微分方程为:
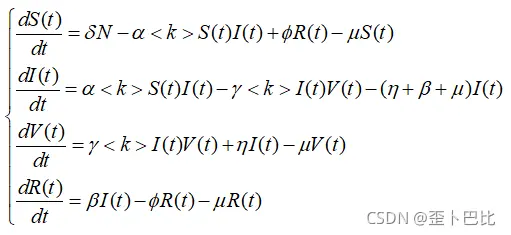
matlab程序:----------------------------
clear;clc;
%各种状态人群参数设置
N = 1;%人口总数
I = 0.2;%感染者
S= N-I;%易感者
R=0;%免疫者
V=0;%潜在变异者
%模型系数设置
a=0.6;%易感者转为感染者系数(感染系数)
b=0.8;%感染者转为免疫者系数(康复系数)
c=0.1;%感染者内部变异
d=0.1;%感染者外部变异
e=0.05;%死亡系数
h=0.2;%免疫者转化为易感者概率
g=0.05;%初始出生率
k=2;%网络平均度(每个个体平均接触其它个体数)
T= 0:100;%迭代总时长
for idx = 1:length(T)-1
S(idx+1) = S(idx)+g*N-a*k*S(idx)*I(idx)+h*R(idx)-e*S(idx);%易感者S迭代
I(idx+1) = I(idx)+a*k*S(idx)*I(idx)-d*k*I(idx)*V(idx)-(c+b+e)*I(idx);%感染者I迭代
V(idx+1) = V(idx)+d*k*I(idx)*V(idx)+c*I(idx)-e*V(idx);%变异者V迭代
R(idx+1) = R(idx)+b*I(idx)-h*R(idx)-e*R(idx);%免疫者R迭代
end
figure
plot(T,S,T,I,T,V,T,R);
grid on;
xlabel('天');ylabel('人数')
legend('易感者S','感染者I','变异者V','免疫者R')
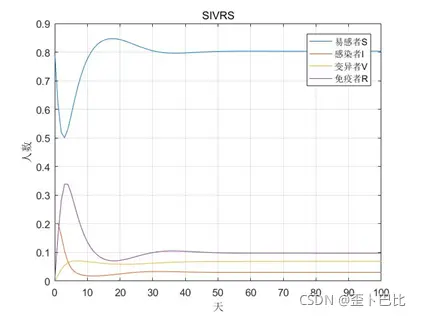
title('SIVRS')
--------------------------------------------
仿真结果:
补充
SEIH
SEIH虽然是为信息传播领域的所提出的,但和病毒传播模型也有很多相似之处,故我们也一并提及。
SEIH模型的特点:
①考虑到信息的二次传播
②与生物病毒传播模型不同,无死亡率(也无出生率),即模型总体量不会发生变化
基于SEIR传播模型,然后根据网络中话题式信息的衍生特性,构建改良式的含有信息机制、信息出现频次及时效性话题式信息传播的SEIHH-SEIR模型。
易感者S接受信息后可以进行选择,一部以α的概率变成移除者,一部分以γ概率变成潜伏者。潜伏者有μ的概率变成感染者, 而在潜伏期的阶段,也有β的概率潜伏者直接转化成免疫状态;再被感染的I状态只能以概率γ转化成免疫者;与SEIR的区别在于,考虑到信息二次传播的可能性,所以处于免疫状态的免疫者会接收到新的消息再次转变成潜在者,则H以概率Θ变成E,进而继续新一轮的传播,其动力学逻辑如下所示:
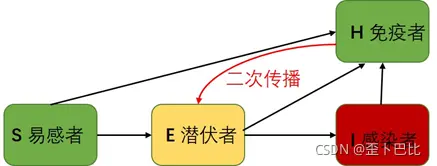
其传播动力学微分方程为:
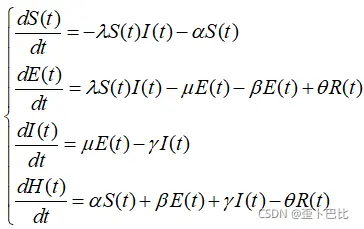
Matlab程序:---------------------
clear;clc;
%各种状态人群参数设置
N = 1;%人口总数
I = 0.2;%感染者
S= N-I;%易感者
H=0;%免疫者
E=0;%潜伏者
%模型系数设置
a=0.2;%易感者转为移除者系数
b=0.6;%易感者转为潜伏者系数
c=0.8;%潜伏者转为免疫者系数
d=0.2;%潜伏者染病系数(潜伏者转为感染者系数)
e=0.7;%感染者转为免疫者系数
f=0.2;%二次传播系数(免疫者变回潜伏者)
T= 0:50;%迭代总时长
for idx = 1:length(T)-1
S(idx+1) = S(idx)-b*S(idx)*I(idx)-a*S(idx);%易感者S迭代
E(idx+1) = E(idx)+b*S(idx)*I(idx)-d*E(idx)-c*E(idx)+f*H(idx);%潜伏者E迭代
I(idx+1) = I(idx)+d*E(idx)-e*I(idx);%感染者I迭代
H(idx+1) = H(idx)+a*S(idx)+c*E(idx)+e*I(idx)-f*H(idx);%免疫者H迭代
end
figure
plot(T,S,T,E,T,I,T,H);
grid on;
xlabel('天');ylabel('人数')
legend('易感者S','潜伏者E','感染者I','免疫者H')
title('SEIH')
------------------------------------------
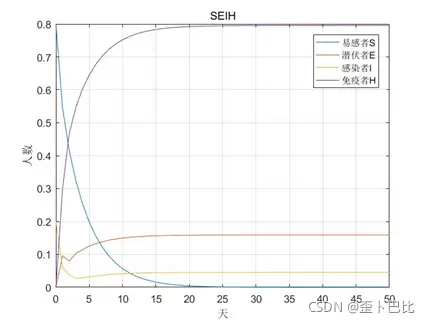
仿真结果:
参考书目
《复杂网络算法与应用》--孙玺菁
(持续更新ing)