带时滞传染病模型分析：基于MATLAB的动力学模型学习笔记‌

/*仅当作学习笔记，若有纰漏欢迎友好交流指正，此外若能提供一点帮助将会十分荣幸*/

在前面的文章中我们提到了几种病毒模型、基本再生数R0等，这里我们将研究带时滞的动力学模型。

摘 要：很多病毒模型因为传染病潜伏期的原因，各种状况之间的转化并不是立刻完成的，而是有存在一个时间差（时滞）。本文将通过一个带时滞的SIR模型，展现带时滞病毒模型的分析方法。

0 搭建模型

在经典SIR模型中，S代表易感状态（也可以理解为未被感染的健康群体），I代表已经被感染的群体，而R代表处于免疫状态的群体（由感染个体I治愈而来的，且假设其治愈后不会再会被感染）。易感个体S有一定几率转化为感染个体I，而感染个体I也有一定几率β变为免疫个体R。SIR模型表达式为：

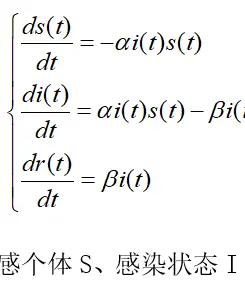
在SIR模型基础上，为了能够充分展现稳定性计算过程中可能会遇到的问题及对应解决方式，我们将构建一个相对复杂的SLA模型（也就是在SIR模型基础上增加条件因素构造而来的）。

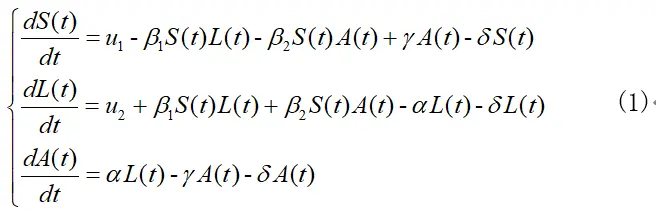
S、L、A分别对应SIR模型中的S、I、R状态，而u1、u2分别代表易感染期和潜伏期病毒的增长率，β1、β2分别代表潜伏期和活跃期的被感染概率，δ为易感染期、潜伏期、活跃期为节点在网络中减少消失的概率，α、γ为状态转移率。 

在上述模型的基础上，为了增加时滞因素，我们在活跃状态A(t)向易感染状态S(t)转移时加入一个时滞tao，转移量为γA(t-tao)，其对应模型为：

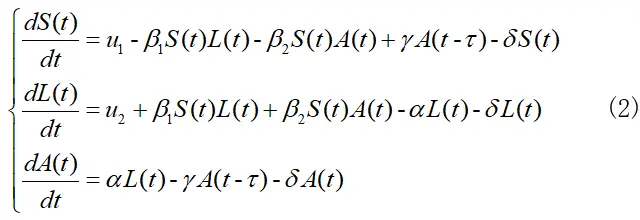
tao实际意义就是遭受到网络病毒侵害的个体恢复到正常状态所需要的时间，也就是接受修复变为易受感染的正常个体时所需要的时间。

1 正平衡点E*的求取

在分析研究一个系统的稳定性时，找到该系统的正平衡点是相当重要的，因为在正平衡点处，系统达到一个临界稳定状态，系统的发展前景也来到了一个十字路口，发散、收敛稳定、周期变换、混沌等等情况都有可能在次之后发生。

1.1初始条件获取

对于一个系统而言，只有在初始条件给定的情况下，才可能继续运算求取其他值。

初始条件1：

对于本文模型，由于为正向系统，易感染期、潜伏期和活跃期的值都不可能为负值，则：

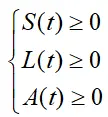
初始条件2：

对于系统（2）来说，当要求取其平衡点，这也就代表系统处于稳定情形，则各种状态下的群体数量暂时保持恒定：

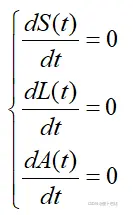
1.2建立初始方程

将初始条件1、2带入到系统（2）中，可得对应条件下的初始方程组：

求解方程组（3），并用L*表示其它两项，可得表达式（4）：

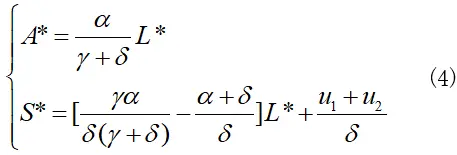
将表达式（4）中的关系再次反代入方程组（3）中，我们可以得到一个关于L*的二元一次方程： 

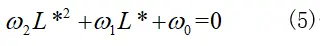
 其中：

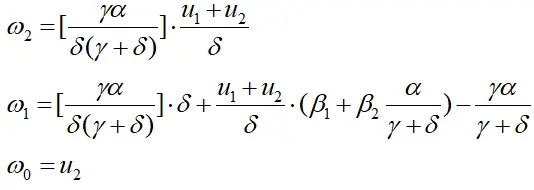
根据初始条件1，对于方程（5）而言，其非负有理解就是为合理解，也可表示为当：

所得L*代入（4）式中，也可得到与之对应的S*、A*得，也就可以得到相应的正平衡点E*(S*、L*、A*) 。

MATLAB计算方法补充：

在实值计算时，可以利用MATLAB中的solve函数求解方程组（3），对应程序为（程序中病毒模型系数可修改，这里值用于举例用）：

2 正平衡条件下的特征矩阵及方程

根据劳斯–赫尔维茨稳定性判据(Routh–Hurwitz stability criterion)，要确定一个系统稳定与否，需要通过其特征方程的系数来判断，因此在讨论稳定性之前需要求得系统的特征方程。

2.1病毒模型的雅可比矩阵

在正平衡点E*(S*、L*、A*) 处，求取模型（2）的雅可比矩阵，即分别对（2）中三个等式关于S、L、A求偏导，可得雅可比矩阵：

其中：

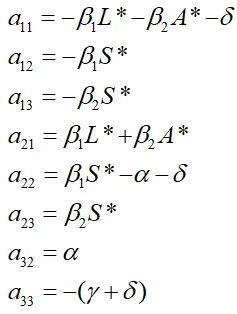
2.2病毒模型的特征矩阵

在2.1中雅可比矩阵（6）基础上，我们可以得到对应特征矩阵：

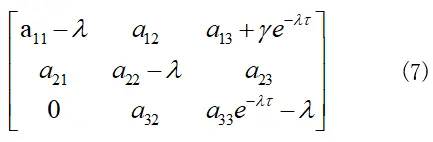
2.3病毒模型的特征方程

对特征矩阵（7）进行计算整理，其相对应特征方程为：

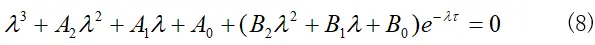
其中：

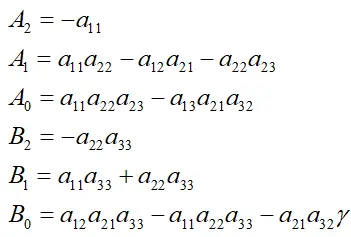
3 传染病模型稳定性分析

3.1劳斯–赫尔维茨稳定性判据

劳斯–赫尔维茨稳定性判据可以通过特征方程的系数来判断系统的稳定性，这里我们简单的举几个例子。

①对于二阶多项式

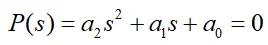
如果所有系数都满足:

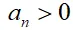
则所有根都在左半平面（特征方程为P(s)的系统稳定）。 

 ②对于三阶多项式

若所有系数都满足：

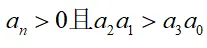
则所有根都在左半平面（特征方程为P(s)的系统稳定）。 

③对于四阶多项式

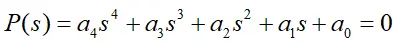
若所有系数都满足：

则所有根都在左半平面（特征方程为P(s)的系统稳定）。

3.2当tao=0时的系统稳定性

当tao=0时，此时2.3中的特征方程（8）可以表示为：

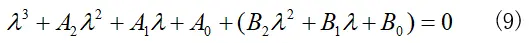
根据劳斯-赫尔维茨判据，当方程同时满足以下条件时：

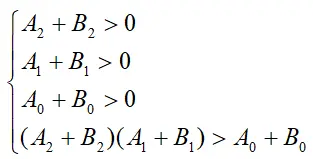
病毒模型局部稳定，也可以将上式化简为：

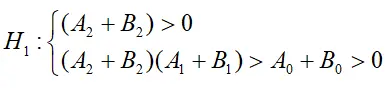
当假设H1成立时，病毒模型（2）处于局部稳定状态。 

3.3当tao>0时的系统稳定性

 令λ=iw为特征方程（8）的根，根据有i和无i项（即有理项和无理项），可以将特征方程（8）简化为：

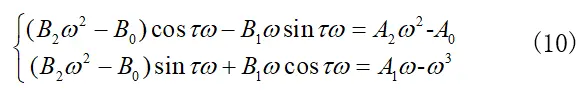
将（10）里面的两式两边同时平方并求和，并利用三角函数关系

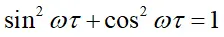
可将（10）式整理为：

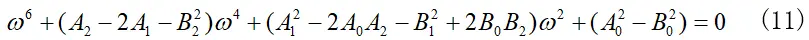
(实值计算时，带入相应数据就可以求得相应根w0)

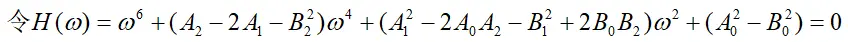
MATLAB计算方法补充：

在求解（11）式时，可以借助solve函数求解

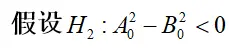
当H2成立时，可以推出H(0)<0，加上

可以得到H(w)=0存在有限个正根

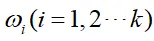
再将根代入到（11）中可得到：

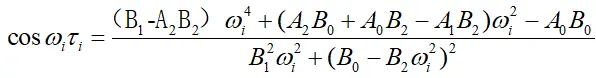
变换得：

3.4 总结

参考文献                           

1. Yang, LX Yang, XF. Propagation Behavior of Virus Codes in the Situation That Infected Computers Are Connected to the Internet with Positive Probability.[J].Discrete Dynamics in Nature and Society,2012,(1):1-13
2. 殷缘圆.一类时滞SLAS网络病毒传播模型稳定性研究.宜春学院学报,2019,41(9):77-79.
3. 武利青,王晓云.一类具有双时滞四维捕食模型的定性分析.中北大学学报:自然科学版,2019(2):97-102.
4. 李大虎,陈淑苹,童欢,朱文文.具有捕食者相互残杀项双时滞系统的Hopf分支.湖北师范学院学报：自然科学版,2011,31(3):76-80.
5. 李颖. HR神经元模型的正平衡点稳定性分析.甘肃科技纵横，2017.01.022 （持续更新ing）