首先明确一点,支持向量机(Support Vector Machine:SVM)就是个二元分类器!所以不要被它看起来花里胡哨的名字吓到。
上次我们说到朴素贝叶斯分类法,它是利用贝叶斯公式去计算在你有这些条件的情况下,你属于某一类的概率是多大。比如已知我的粉丝群体是16-25岁居多,此时你是我的粉丝,你在16-25岁之间的概率就比较大。算法可能(如果不考虑其他变量)把你分类为“青年”。
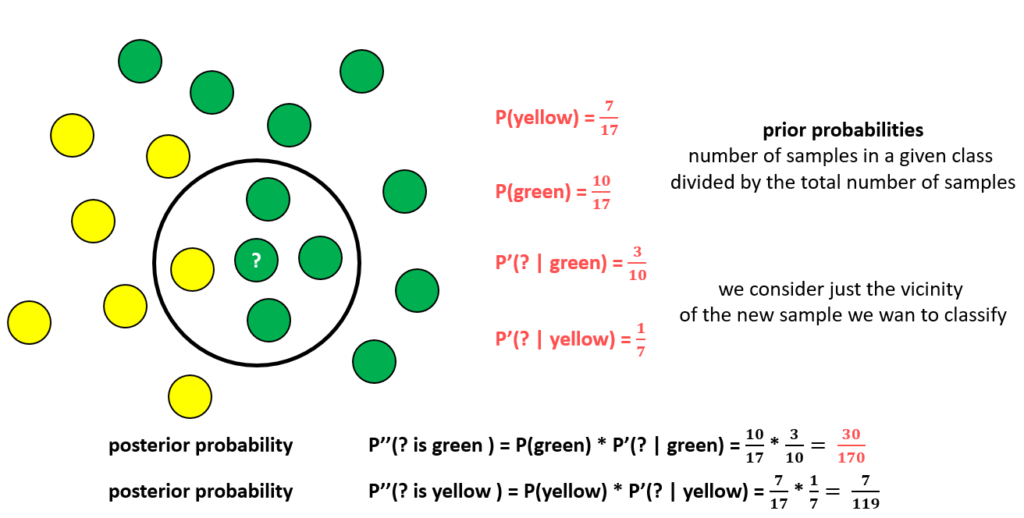
这次说的支持向量机方法,相比贝叶斯方法,目的是一样的,给数据分类;但原理是完全不一样的。支持向量机方法的原理是非常直观的:一组分布在空间中的点,你要寻找一个平面,使得每个点到这个平面的距离的和,最大。也就是下面这张图:
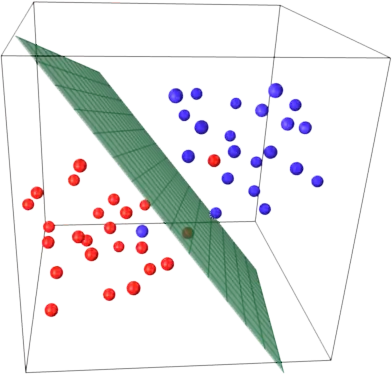
这个平面确定后,分类模型就确定了:平面的一侧为一类,另一侧为另一类。之后的新点都可以通过把它们的空间位置代入平面方程来判断它们属于哪类:如果是在平面上,则等于0,如果在某一侧,那么大于0,如果在另一侧,则小于0。
现在这个图表示的是二维空间下的平面,学过基本的几何知识可知,平面的表达式为:
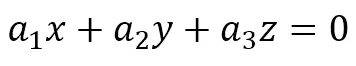
其中(a1,a2,a3)为垂直于这个平面的法向量。
那么什么是超平面呢?我们注意到,对于一个三维空间,平面是一个二维几何物体,其把三维空间分成了两个三维空间。那么超平面就是,对于一个n维空间,一个(n-1)维的几何体,将空间分成两个n维空间。
例如,对于一个二维平面,超平面就是一维直线,将平面分成两个部分;对于一个一维直线,超平面就是一个点,将直线分成两部分。
那么向上推广,对于n维度空间:
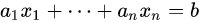
我们同样有超平面:
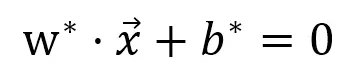
于是我们的分类器就是下图公式,也就是把数据点的坐标代入平面的公式,看它是大于0,还是小于0。y=sign(x)就是一个函数,当x大于0,y就等于1;当x小于0,y就等于-1.
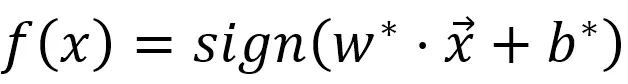
线性可分支持向量机
那么这个方法为什么叫“支持向量机”呢?原因就在于我们根据数据求解超平面系数的过程。
最开始我们说过:支持向量机的原理是给定一组分布在空间中的点,你要寻找一个平面,使得每个点到这个平面的距离的和最大。
那么问题来了,对于高维度空间,我们如何定义“距离”?我们可以仍然直观地采用几何距离,即数据到平面的垂直向量的长度。
即:
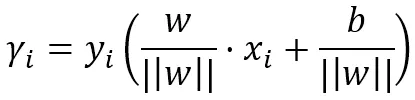
其中下标i表示第i个数据点。||w||表示w的2范数,也就是所谓平方相加开根号,也就是所谓“距离”。在N个坐标点中,一定有一个距离超平面最小的距离,我们定义它为:
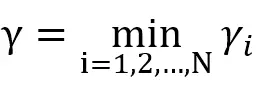
我们希望找到一个平面,使得这个最小值最大。
支持向量呢,就指的是距离超平面最近的点对应的向量,它们决定了超平面的形状。只要支持向量确定了,其他点的位置变动并不会影响超平面的形状。
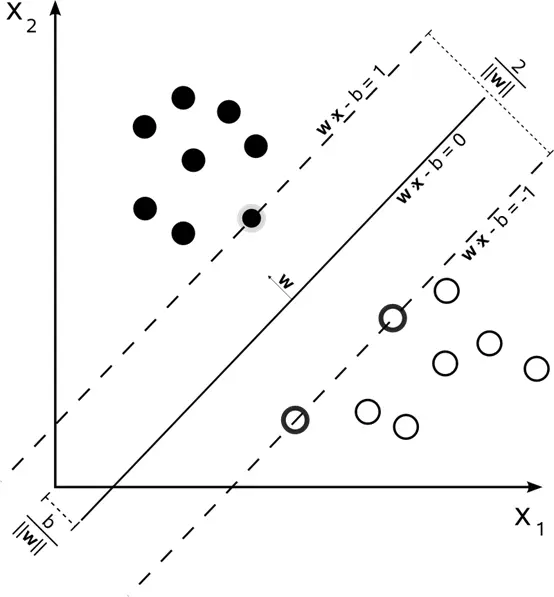
支持向量
好了,所以一个数学问题就被提炼出来了:
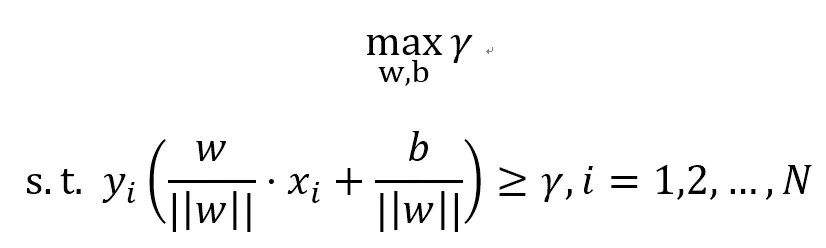
这是一个约束最优化问题,也就是在约束条件下,寻找最大或者最小值。这类问题可以使用拉格朗日乘子法解决。
好了,中间过程并不是很重要(写上也不能一下子看懂,我也不觉得有人会认真反复研读一篇B站的文章),我直接出结果
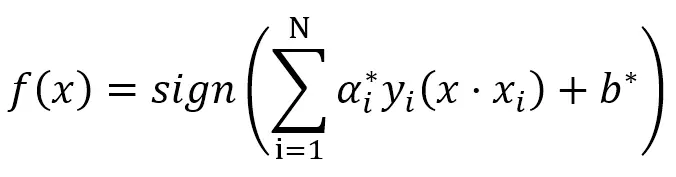
其中a_i是引入的拉格朗日乘子,b是超平面的常数参数。x_i是训练集中的自变量,y_i是训练集中的分类标签。
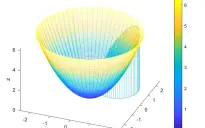
稍微延伸一下,对于一个平面切不开的数据集怎么办呢,我们可以对向量做拉伸和缩短,使得一个曲面可以被拉成一个“平面”,如图所示:
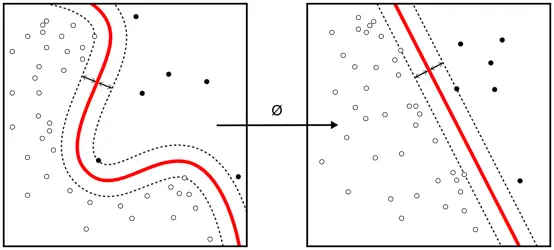
其中每个向量都会有一个拉伸系数。
最后说一下matlab实现方法:
流程还是一样的:读取训练集→跑出模型→选择测试集→看误识别率
读取数据:
data=xlsread("data.xls",'A2:AJ500');
X=data(:,1:6);%自变量
Y=data(:,7);%分类标签
SVMModel = fitcsvm(X,Y,'Standardize',true,'KernelFunction','RBF',...
'KernelScale','auto');
resubLoss(SVMModel,'LossFun','ClassifErr')%误识别率data_test=xlsread("data.xls",'A501:AJ1024');%验证集
X=data_test(:,1:6);%自变量
Y=data_test(:,7);%分类标签
loss(SVMModel,newX,newY)%验证模型对验证集的误识别率
跑完以后我们看一下模型参数
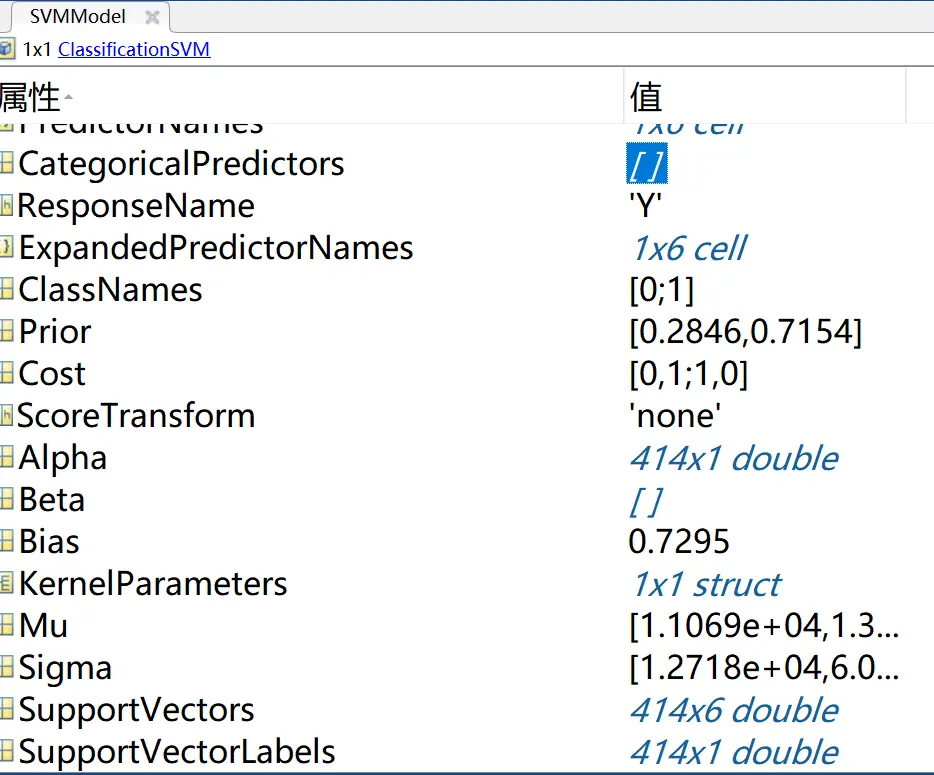
Prior就是根据数据分类计算出的先验概率,Alpha就是前面提过的,用于模型构建的拉格朗日乘子。Mu就是数据的均值,Sigma就是数据的标准差
全部系数解释:
https://ww2.mathworks.cn/help/stats/classificationsvm.html
另外你还可以画一下分类情况图:
isLabels1 = resubPredict(SVMModel);
ConfusionMat1 = confusionchart(Y,isLabels1);
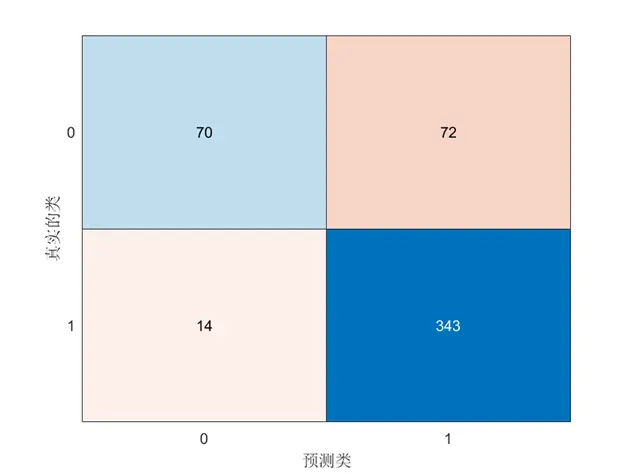
分类情况图
对角部分就是分类正确的,非对角部分就是误分类的。
参考资料:
MATLAB说明文档
https://ww2.mathworks.cn/help/stats/fitcsvm.html
https://ww2.mathworks.cn/help/stats/fitcnb.html
https://ww2.mathworks.cn/help/stats/classificationsvm.html
维基百科