灰色关联度分析(grey relation analysis)
作用:
两个变量之间的关联关系;截面数据的相关性,或者两个变量在时间序列上的变化一致性。
适用条件:
相关分析最小样本量需求为30,当样本量过小时,可以使用灰色关联度分析。
步骤:
示例数据:
clc;clear;
Data=[376 62 89 74 65 86;373 66 73 57 85 92;382 72 83 78 89 60;368 86 58 58 91 75;329 91 63 56 62 57;373 58 60 92 94 69;398 90 88 86 72 62;339 95 72 56 61 55;377 83 55 85 67 87;389 58 90 84 89 68]
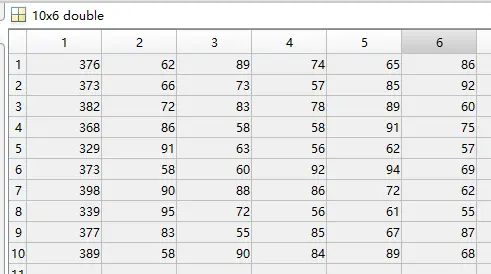
第一列为因变量,后面为5个自变量。
Step1 :数据预处理:采用均值化方法去除量纲的影响。
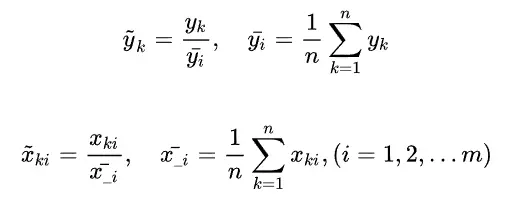
每个变量的样本,依次除以该变量的平均值即可。
%第一步,对变量进行预处理,消除量纲的影响
r=size(Data,1);
c=size(Data,2);
avg=repmat(mean(Data),r,1);
data=Data./avg;

mean去量纲结果
step2: 确定母序列和子序列:
对具有映射关系的变量而言:母序列就是你的因变量,子序列就是自变量。子序列影响母序列。
对于两个变量关联性分析,就是相对的。

因变量只有一个,m个样本

自变量有n个,m个样本
step3: 计算子序列和母序列的关联系数:
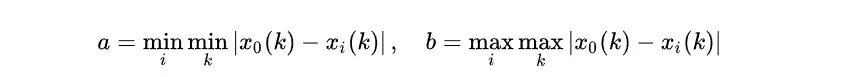
%定义参考序列和比较序列
% 前面的自变量和因变量都放成了一个矩阵,第一列是因变量,后面都是自变量,这里把它们分开。
Y=data(:,1);%参考序列
X= data(:,2:c);%比较序列
% X= data(:,2); % 如果只有一个自变量,或者是两个变量算关联性,则都是1列。
% 此处开始对应上面的公式:
Y2=repmat(Y,1,c-1);%把参考序列向右复制到c-1列,因变量
对Y进行重复扩充,方便后续对应做减法。
原始的Y

扩充后的Y
* 注:也可以不扩充用循环做,但是没必要,能矩阵运算的何必倒退回向量。
absXi_Y=abs(X-Y2); % 每个自变量就有一个对应的Y来矩阵减法就行
a=min(min(absXi_Y));% 公式中的最小值
b=max(max(absXi_Y));% 公式中的最大值
% 两个min和两个max与公式对应。一个就得到abs的一个行向量,两次min或max就得到整个abs矩阵的最大值或最小值。
* Mark:这里先mark1,后面另一个问题讨论中会返回。
step 4:计算关联度

前面a,b算出来了,p也有了,直接算即可得到结果了。
p=0.5;%分辨系数取0.5
gamma=(a+p*b)./(absXi_Y+p*b)%计算比较序列中每个指标与参考序列的关联度
ans = mean(gamma) % 得到结果
//------------------------------------灰色关联度计算结束--------------------------------------------------//
灰色关联度计算变量重要性和2个变量相关性的结果一致吗?
答案:不一致。
一个是包含多个自变量的全局关系,一个是2个变量相对而言的局部关系。
如下图:

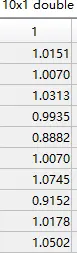
上述示例中5个自变量对因变量的相对关联程度
那么,如果我现在只有Y和一个X,也就是说不存在自变量和因变量关系,就是想探究2个变量之间的关联关系,X的赋值修改为:
% X= data(:,2); % 只取第一个自变量,计算结果为:

不是0.5091
原因回到前面Mark处:
求第对于多个自变量而言,二个min和max的时候,返回值为5个自变量中最小或最大的那一个;只有一个自变量,则只能返回本身的最大值或最小值。对于存在映射关系的重要性排序而言,必须考虑全局关系,对应于两个min或max;对于两个变量互相关联,无关x和y(加上绝对值减数和被减数调换位置结果都一样),因此只取一个min或max即可(没必要改成一个,因为加一层还是一样的结果,并且同时2种情况都可以用)。
所以,不过是一个是全局关系,一个是两个变量本身的关系。不是不一致就是算错了,而是原理上本就是2回事,结果是对的。