这是一篇写于去年的结课文章,主要讨论了图像分析和MATLAB方面的课题。借鉴了很多相关的参考文献、资料、学校图书馆的书籍(具体在文末呈现)。鉴于视频中只有对文章的大概描述,所以就把文章整理了一下放在这里,就当分享了。做的不太完美,请多多指教!


1.概述
1.1研究背景
图像增强技术是图像处理领域中一项很重要的技术。对图像恰当的增强,可以在去除图像噪声的同时能同时较好地保护图像特征,使图像更加清晰明显,从而提供给我们准确的信息。图像增强的方法是通过一定手段对原图像附加一些信息或变换数据,有选择地突出图像中感兴趣的特征或者抑制(掩盖)图像中某些不需要的特征,使图像与视觉响应特性相匹配。在图像增强过程中,不分析图像降质的原因,处理后的图像不一定逼近原始图像。
1.2研究意义
人类传递信息的主要媒介是语言和图像。据统计在人类接受的各种信息中视觉信息占80%,所以图像信息是十分重要的信息传递媒体和方式。图像传递系统包括图像采集、图像压缩、图像编码、图像存储、图像通信、图像显示这六个部分。在实际应用中每个部分都有可能导致图像品质变差,使图像传递的信息无法被正常读取和识别。例如,在采集图像过程中由于光照环境或物体表面反光等原因造成图像整体光照不均,或是图像采集系统在采集过程中由于机械设备的缘故无法避免的加入采集噪声,或是图像显示设备的局限性造成图像显示层次感降低或颜色减少等等。因此研究快速且有效地图像增强算法成为推动图像分析和图像理解领域发展的关键内容之一。提高图像的视感质量,像对图像的亮度,彩色变换,增强,抑制某些成分,对图像进行几何变换等,来改变图像的质量。提取出图像中所包含的某些特征或者特殊信息,来为计算机分析图像提供便利。提取特征或信息的过程是模式识别或计算机视觉的预处理。提取的特征可以包括很多方面,如频域特征,灰度或颜色特征,边界特征,区域特征,纹理特征,形状特征,拓扑特征和关系结构等。
1.3研究现状
1.3.1图像增强分类
频率域法:基于频域的算法是在图像的某种变换域内对图像的变换系数值进行某种修正,是一种间接增强的算法,它把图像看成一种二维信号,对其进行基于二维傅里叶变换的信号增强。采用低通滤波(即只让低频信号通过)法,可去掉图中的噪声;采用高通滤波法,则可增强边缘等高频信号,使模糊的图片变得清晰。
空间域法:基于空域的算法处理时直接对图像灰度级做运算。空间域法中具有代表性的算法有局部求平均值法和中值滤波(取局部邻域中的中间像素值)法等,它们可用于去除或减弱噪声。基于空域的算法分为点运算算法和邻域去噪算法。点运算算法即灰度级校正、灰度变换和直方图修正等,目的或使图像成像均匀,或扩大图像动态范围,扩展对比度。邻域增强算法分为图像平滑和锐化两种。平滑一般用于消除图像噪声,但是也容易引起边缘的模糊。常用算法有均值滤波、中值滤波。锐化的目的在于突出物体的边缘轮廓,便于目标识别。常用算法有梯度法、算子、高通滤波、掩模匹配法、统计差值法等。
1.3.2应用领域
图像增强处理的应用已经渗透到医学诊断、航空航天、军事侦察、指纹识别无损探伤、卫星图片的处理等领域.如对x射线图片、CT影像、内窥镜图像进行增强,使生更容易从中确定病变区域,从图像细节区域中发现问题,对不同时间拍摄的同一地区的遥感图片进行增强处理,侦查是否有敌人军事调动或军事装备及建筑出现,在煤矿工业电视系统中采用增强处理来提高工业电视图像的清晰度,克服因光线不足,灰尘等原因带来的图像模糊、偏差等现象,减少电视系统维护的工作量.图像增强技术的快速发展同它的广泛应用是分不开的,发展的动力来自稳定涌现的新的应用,可以预料,在未来社会中图像增强技术将会发挥更为重要的作用。
2.灰度变换图像增强算法
灰度变换灰度变换可使图像动态范围增大,对比度得到扩展,使图像清晰、特征明显,是图像增强的重要手段之一,它主要利用点运算来修正像素灰度,由输入像素点的灰度值确定相应输出点的灰度值,是一种基于图像变换的操作.灰度变换不改变图像内的空间关系,除了灰度级的改变是根据某种特定的灰度变换函数进行之外,可以看作是“从像素到像素”的复制操作.基于点运算的灰度变换可表示为:
G(X.Y)-TUF(.y)l(3.10)
其中T被称为灰度变换系数,它描述了输入灰度值和输出灰度值之间的转换关系。一旦灰度变换函数确定,该灰度变换就被完全确定下来。
灰度变换包含的方法很多,如逆反处理、阔值变换、灰度拉伸、灰度切分、灰度线修正、动态范围调整等,且然它们对图像的处理效果不同,但处理过程中都运用了点运算,通常可分为线性变换、分段线性变换、非线性变换。
2.1线性灰度变换
比例线性变换是对每个线性段逐个像素处理,它可以把原图像的灰度值动态范围按照线性关系式扩展到指定范围或整个动态范围。
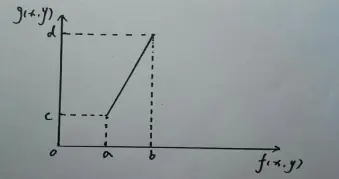
假设给定的是两个灰度区间,如下图:
(1)
原图像f(x,y)的灰度范围为[a,b],我们希望变换后的图像g(x,y)的灰度扩展为[c,d],线性变换简单的线性灰度变换法可表示为:
g(x,y)=(d-c/b-a)[f(x,y)-a]+c
经过线性灰度变化法,可以把输入图像的某个亮度值区间[a,b]扩展为输出图像的亮度值区间[c,d],b和a分别是输入图像亮度分量的最大值和最小值,d和c分别是输出图像亮度分量的最大值和最小值。采用比例线性灰度变换对图像每一个像素灰度进行线性拉伸,会有效地改善图像视觉效果。
若图像灰度在0~M范围内,图像中大部分像素的灰度级分布在区间[a,b]内,M为原图的最大灰度级,只有很小一部分的灰度级超过了此区间,则为了改善增强效果,如下图:

(2)
数学模型为:
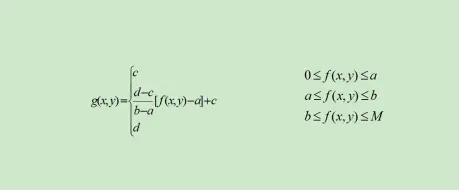
(3)
由于人眼对灰度级别的分辨能力有限,只有当相邻像素的灰度值相差到一定程度时才能被辨别出来。通过上述变换,图像中相邻像素灰度的差值增加,例如在曝光不足或过度的情况下,图像的灰度可能会局限在一个很小的范围内,这时得到的图像可能是一个模糊不清,似乎没有灰度层次的图像。采用线性变换对图像中每一个像素灰度作线性拉伸,将有效改善图像视觉效果。注意,这种变换扩展了[a,b]区间的灰度级,但是将小于或等于a和大于或等于b范围内的灰度级分别压缩为c和d,这样使图像灰度级在上述[0 ,a]和[b,M]两个范围都各自变成c,d灰度级分布,从而可以得到我们想要的信息。
线性灰度变换增强程序:
clc;
clear all;
I = imread(' D:\1.jpg'); % 读入原图像
I = im2double(I); % 转换数据类型为double
[M,N] = size(I); % 计算图像面积
figure(1); subplot(121); % 打开新窗口,设置图像位置
imshow(I); % 显示原图像
title('原图像'); % 定义标签
Fa = 6; Fb = -160;
O = Fa .* l+ Fb/255; % 线性变换公式
figure(1);subplot(122);
imshow(O);
title('灰度变换后的图像');
效果如下:

(4)
2.2分段线性变换
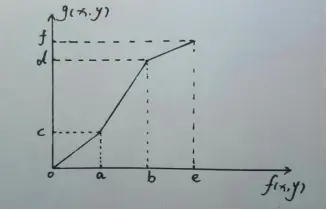
为了突出图像中感兴趣的目标或灰度区间,相对抑制那些不感兴趣的灰度区间,把线性灰度变换原理引申应用,可采用分段线性变换,将图像灰度区间分成两段甚至多段分别作线性变换。分段线性变换的优点是可以根据用户的需要,拉伸特征物体的灰度细节,相对抑制不感兴趣的灰度级。采用分段线性法,可将需要的图像细节灰度级拉伸,增强对比度,将不需要的细节灰度级压缩。在进行变换时,把0~255整个灰度值区间分为若干线段,每一个直线段都对应一个局部的线性变换关系。如下图:
(5)
数学模型:
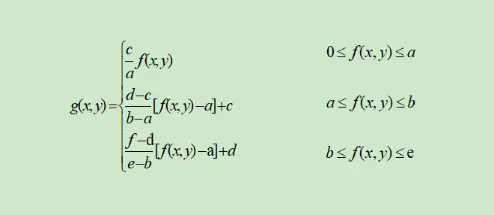
(6)
在MATALB中通过调用imread函数和imshow函数来实现分段线性灰度变换增强,举个例子:
分段线性变换增强算法代码:
I=imread('D:\1.jpg'); % 读入原灰度图像
[m,n,k]=size(I);
subplot(1,3,1);%把生成的图像排成一行三列
imshow(I);
title('原图像'); %显示原灰度图像
Ig=rgb2gray(I); %生成I的灰度图像
subplot(1,3,2);
imshow(Ig);
title('灰度图像');
I=double(I);%转换成double型,避免精度丢失
Max=max(max(Ig)); %求出最大灰度
J=zeros(m,n,3); %生成一个三位矩阵,后面用于存储变换后的图像
a=100;
b=200;
c=10;
d=245;
k1=c/a;
k2=(d-c)/(b-a);
k3=(255-d)/(Max-b);
for i=1:m
for j=1:n
for k=1:3
if I(i,j,k)<=100
J(i,j,k)=k1*I(i,j,k);
else if 100<I(i,j,k)<=200
J(i,j,k)=k2*(I(i,j,k)-100)+50;
else
J(i,j,k)=k3*(I(i,j,k)-200)+220;
end
end
end
end
end
J=uint8(J);%把double型的J转换成unit8型
subplot(1,3,3),
imshow(J);
title('分段线性灰度变换后的图像');
效果如下:

(7)
2.3非线性变换
非线性拉伸不是对图像的整个灰度范围进行扩展,而是有选择的对某一灰度范围进行扩展,其他范围的灰度值则有可能被压缩。非线性拉伸利用变换函数的数学性质实现对不同灰度值区间的扩展与压缩。利用一些非线性函数,例如平方,对数,指数函数等作为映射函数时,可以实现图像灰度的非线性变换。如下图:
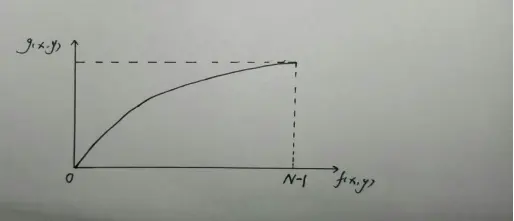
(8)
对数变换,是指输出图像的像素点的灰度值与对应的输出图像的像素灰度值之间为对数关系,其一般公式为:
g(x,y)=a+ln[f(x,y)+1]/blnc
式中a,b,c 都是可以选择的参数,式中f(x,y)+1是为了避免对0求对数,确保ln[f(x,y)+1]≥0。当f(x,y)=0时,ln[f(x,y0+1),则y=a,则a为y轴上的截距,确定了变换曲线的初始位置的变换关系b,c,两个参数确定变换曲线的变换速率。对数变换扩展了低灰度区,压缩了高灰度区,能使低灰度区的图像较清晰地显示出来。
非线性灰度变换增强代码:
clc;
clear all;
I=imread('D:\1.jpg'); %读入图像
J=double(I);%将图形矩阵转化为double型
J=40*(log(J+1));%把图像对数转换
H=uint8(J);%double型转化为uint8型
subplot(1,2,1);
imshow(I);
title('原图像');%显示对数变换前的图像
subplot(1,2,2);
imshow(H);
title('对数变换后的图像');%显示对数变换后的图像
效果如下:

(9)
3.总结
空域增强在数字图像处理中起到对图像灰度的拉伸、压缩变换的作用,目前这种方法在处理图像灰度值方面得到广泛的运用。灰度变换是空域变换的一种重要方式,可使图像对比度扩展,图像清晰,特征明显。
不足:线性灰度变换计算简单,仅适用于灰度级变化比较平滑的图像,并且有可能受到个别极限灰度级的不良影响。分段线性增强更适用于有选择性的对图像进行局部线性对比度增强,需要更多的用户输入。

相关资料如下:
[1] 刘刚. MATLAB数字图像处理[M].北京:机械工业出版社. 2010:34-45.
[2] 王家文.MATLAB 6.5 图形图像处理[M].上海:国防工业出版社. 2009:6-14.
[3] 王晓丹.MATLAB系统分析[M].西安:西安电子科技大学出版. 2000:168-220.
[4] yang fan,Pu zhaobang. Application of Fuzzy Logic in Weighted Information Fusion of Hand Shapes and Palm Print [J],JOURNAL OF ELECTRONICS(CHINA) ,2004,21(6):511-514
[5] 郝文化.MATLAB图像处理[M].河北:中国水利水电出版社. 2004:66-78.
[6] 苏金明. MATLAB图形图像[M].四川:成都电子工业出版社. 2005:87-90.
[7] 杨志刚等.现代通信原理[M].清华大学出版社. 2008: 66-89.
[8] 杨帆等.数字图像处理及应用.化学工业出版社.2013.
[9] 李圣勤. MATLAB7.0实用教程[M].机器工业出版社. 2006: 90-118.
[10] 朱习军. MATLAB在信号与系统与图像处理中的应用[M].电子工业出版社. 2002: 34-50.
[11]数字图像增强中灰度变换方法研究[J]. 余章明,张元,廉飞宇,陈得民,王红民. 电子质量. 2009(06)
[12]图像增强方法的研究以及应用[D]. 刘锦辉.湖南师范大学 2009