TensorFlow 2.0入门指南

图片是一个三阶张量，其维度为高，宽以及通道数（红，绿，蓝）。

登录后复制

import tensorflow as tfimage=tf.image.decode_jpeg(tf.read_file("./1.jpg"),
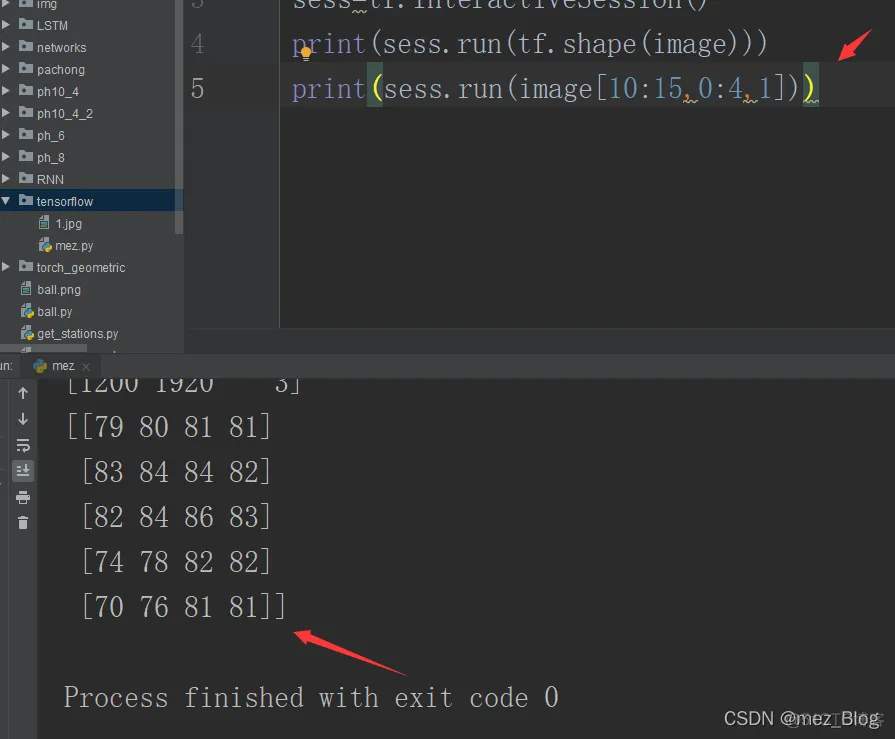
channels=3)sess=tf.InteractiveSession()print(sess.run(tf.shape(image)))1.2.3.4.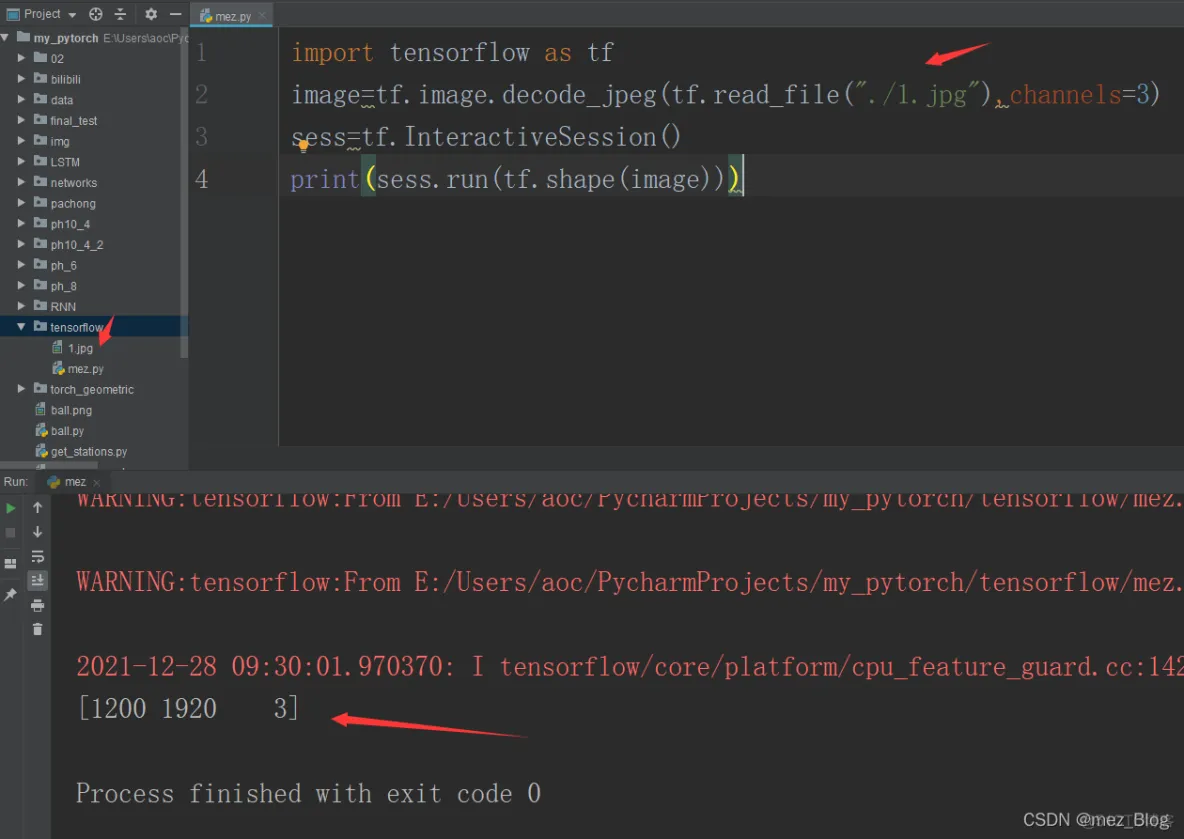

可以生成各种类型的张量，比如固定张量、随机张量以及序列张量。

5.1固定张量

下面是固定张量：

登录后复制

import tensorflow as tfsess=tf.Session()A=tf.zeros([2,3])print(sess.run(A))B=tf
.ones([4,3])print(sess.run(B))1.2.3.4.5.6.7.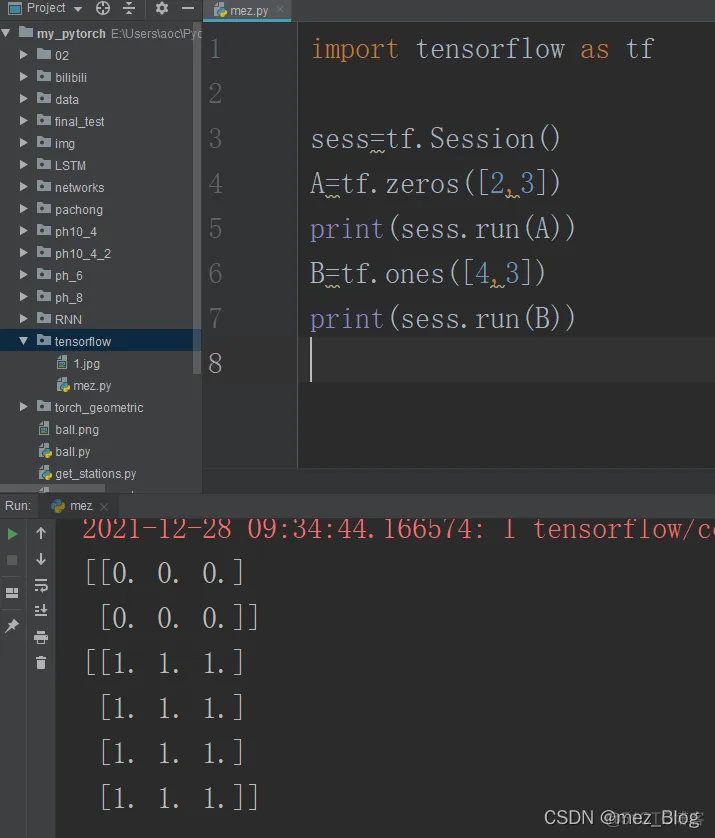

tf.fill创建一个形状为[2*3]的数值唯一的张量。

tf.diag创建一个具有特定对角元素的对角矩阵。

tf.constant创建一个常数张量。

5.2序列张量

tf.range创建一个开始于给定值并具有给定增量的数字序列。

tf.linspace创建一个等间距值的数字序列。

登录后复制

G=tf.range(start=6,limit=45,delta=3)print(sess.run(G))H=tf.linspace(10.0,92.0,5)print(sess.run(H))1.2.3.4.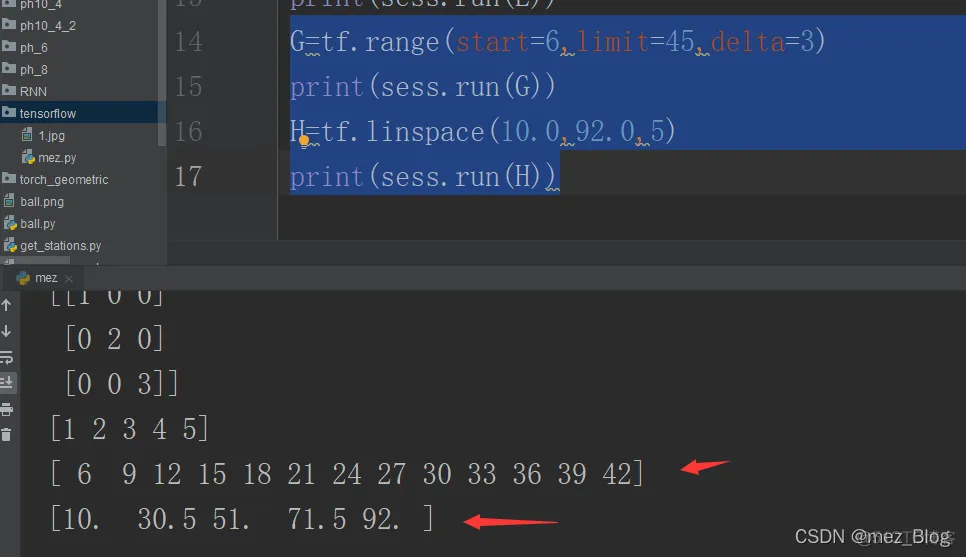

5.3随机张量

登录后复制

import tensorflow as tfsess=tf.Session()a=tf.random_uniform([2,3],
minval=0,maxval=4)print(sess.run(a))b=tf.random_normal([2,3],mean=5,
stddev=4)print(sess.run(b))c=tf.random_shuffle(tf.diag([3,-2,4]))print(sess.run(c))d=tf
.random_crop(tf.diag([3,-2,4]),[3,2])print(d)1.2.3.4.5.6.7.8.9.10.11.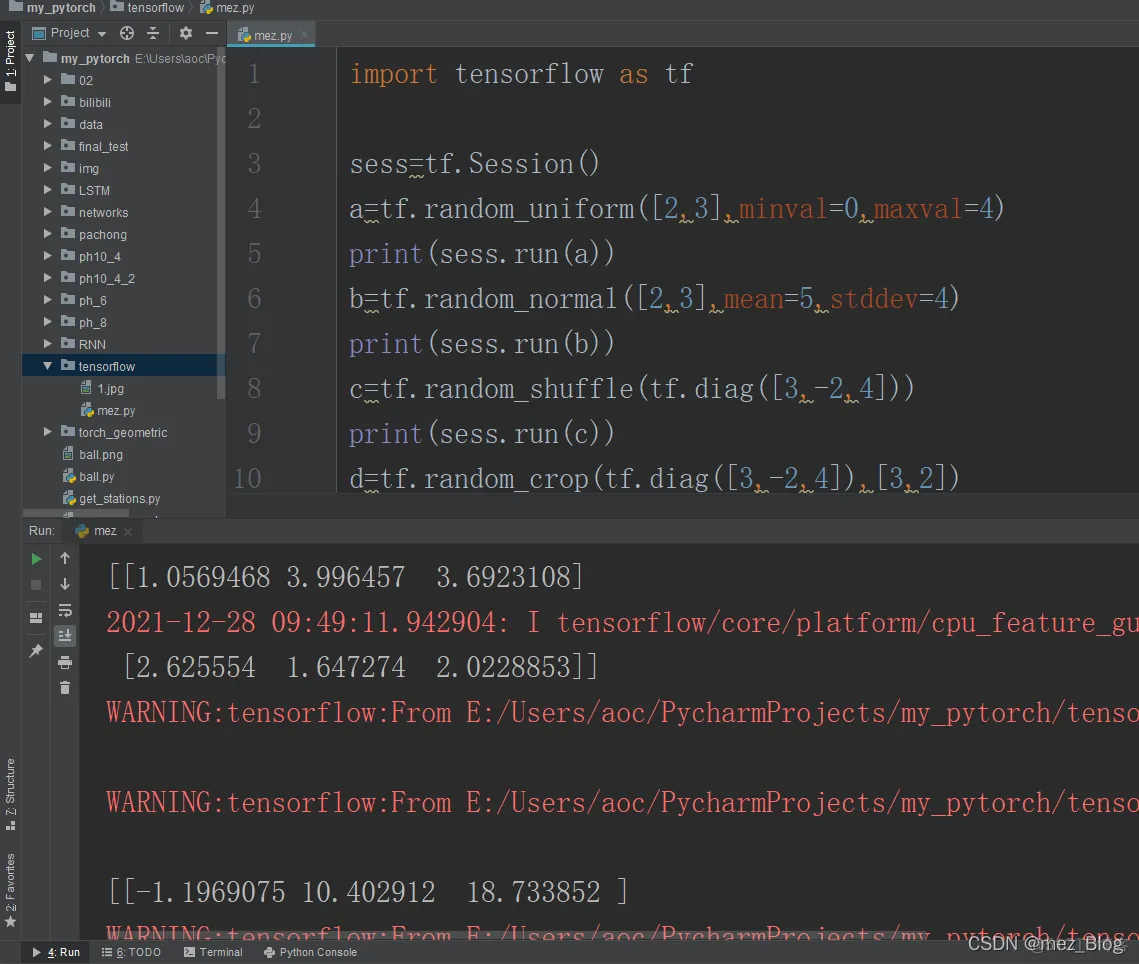

tf.random_uniform在给定范围内服从均匀分布生成随机值。

tf.random_normal服从给定均值和标准差的正态分布生成随机值。

tf.random_shuffle为随机打乱。

tf.random_crop为随机裁剪。

6.矩阵操作

一旦对创建张量感到自如了，就可以使用矩阵（二维张量）来工作了。

登录后复制

import tensorflow as tfimport numpy as npsess=tf.Session()a=tf
.random_uniform([3,2])# print(sess.run(a))b=tf.fill([2,4],3.5)
# print(sess.run(b))c=tf.random_normal([3,4])print(sess.run(a))
# d=tf.random_crop(tf.diag([3,-2,4]),[3,2])print(sess.run(b))print(sess.run(tf
.matmul(a,b)+c))print(sess.run(tf.matmul(a,b)))1.2.3.4.5.6.7.8.9.10.11.12.13.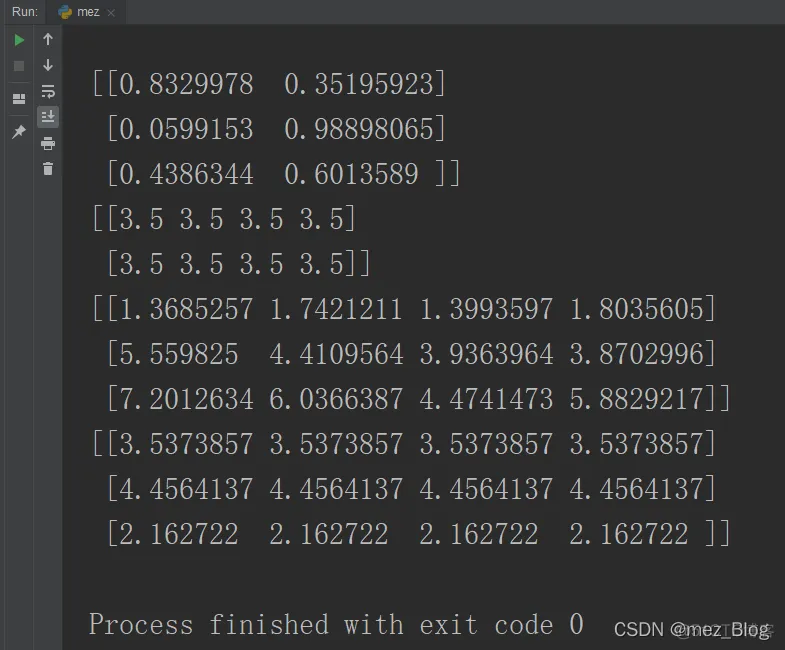

7.损失函数

损失函数（代价函数）是用来最小化已得到模型每个参数的最优值的。比如说，为了用预测器（x）来预测目标（y）的值，需要获取权重值（斜率）和偏置量（y截距）。得到斜率和y截距最优值的方法就是最小化代价函数/损失函数/平方和。对于任何一个模型来说，都有很多参数，而且预测或进行分类的模型结构也是通过参数的数值来表示的。

你需要计算模型，并且为了达到这个目的，需要定义代价函数（损失函数）。最小化损失函数就是为了寻找每个参数的最优值。对于回归/数值预测问题来说。L1或L2是很有用的损失函数。对于分类问题来说，交叉熵是很有用的损失函数。softmax或者sigmoid交叉熵都是非常流行的损失函数。

下面是演示代码：

登录后复制

import tensorflow as tfimport numpy as npsess=tf.Session()pred=np
.asarray([0.2,0.3,0.5,0.6,0.8,12.0,13.0,7.4,3.9,2.3])x_val=tf
.convert_to_tensor(pred)actual=np.asarray([0.1,0.4,0.6,9.0,11.0,12.0,3.4,7.1,3.8,2.0])
#MSE Lossl2=tf.square(pred-actual)l2_out=sess.run(tf.round(l2))print(l2_out)
#l2 loss:l1=abs(pred-actual)l1=tf.abs(pred-actual)l1_out=sess.run(l1)print(l1_out)
#交叉熵损失soft=tf.nn.sigmoid_cross_entropy_with_logits(logits=l1_out,labels=l2_out)print(sess.run(soft))1.
2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.

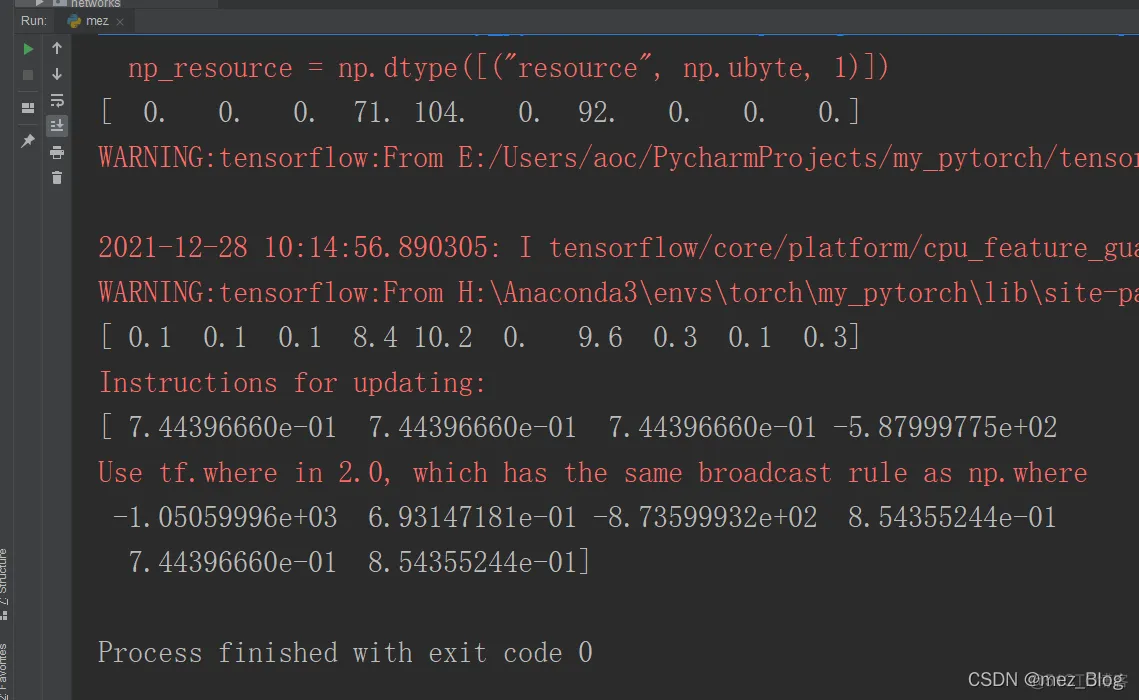
8.优化器

现在我们已经知道需要使用损失函数来获得模型参数的最优值了。那么，到底怎样求得最优值呢？

开始我们假定了模型（线性回归等）中权重和偏置量的初始值。现在你需要找到抵达参数最优值的方法。优化器就是找到参数最优值的方法。在每一次迭代中，参数值朝优化器致命的方向去更新。加入你有16个权重值（w1.....w16）和4个偏置量（b1,b2,b3,b4）.开始你可以假定每个权重值和偏置量为0（或者是1，或者是其它任意的数值）。优化器时刻记录这最小化的目标，决定w1（以及其它参数）在下一次迭代中应该是增加还是减少。在很多次迭代之后，w1（以及其它参数）将会稳定到最优值。

换言之，TensorFlow或者每一个其它的深度学习框架都会提供优化器来逐步更新每一个参数的值，已达到最小损失函数的目的。优化器的目标就是给定权重和偏置量在下一次迭代时变化的方向。假定有64个权重值和16个偏置量，你尝试在每次迭代中改变其值（在反向传播中），在尝试最小化损失函数的很多次迭代之后，应该可以得到正确的权重值和偏置量的值。

为模型选择一个最好的优化器，收敛快并且能学到合适的权重和偏置量的值，是一个需要技巧的事情。

自适应技术（Adadelta等）对于复杂的神经网络模型来说是很好的优化器，收敛更快。大多数情况下，Adam可能是最好的优化器。Adam还优于其他自适应技术，但是其计算成本很高。对于系数数据集来说，一些方法如SGD、NAG以及momentum不是最好的选择，能自适应调整学习率的方法才是。一个附加的好处就是不需要调整学习率，使用默认的学习率就可以达到最优解。

下面是演示代码：

登录后复制

import tensorflow as tfx=tf.Variable(3,name='x',
dtype=tf.float32)log_x=tf.log(x)log_x_squared=tf
.square(log_x)optimizer=tf.train.GradientDescentOptimizer(0.7)train=optimizer
.minimize(log_x_squared)init=tf.global_variables_initializer()with tf
.Session() as sess:    sess.run(init)    print("starting at","x:",sess
.run(x),"log(x)^2:",sess.run(log_x_squared))    for step in range(10):        sess.run(train)        
print("step",step,"x:",sess.run(x),"log(x)^2",sess.run(log_x_squared))1.2.3.4.5.6.7.8.9.10.11.12.13.

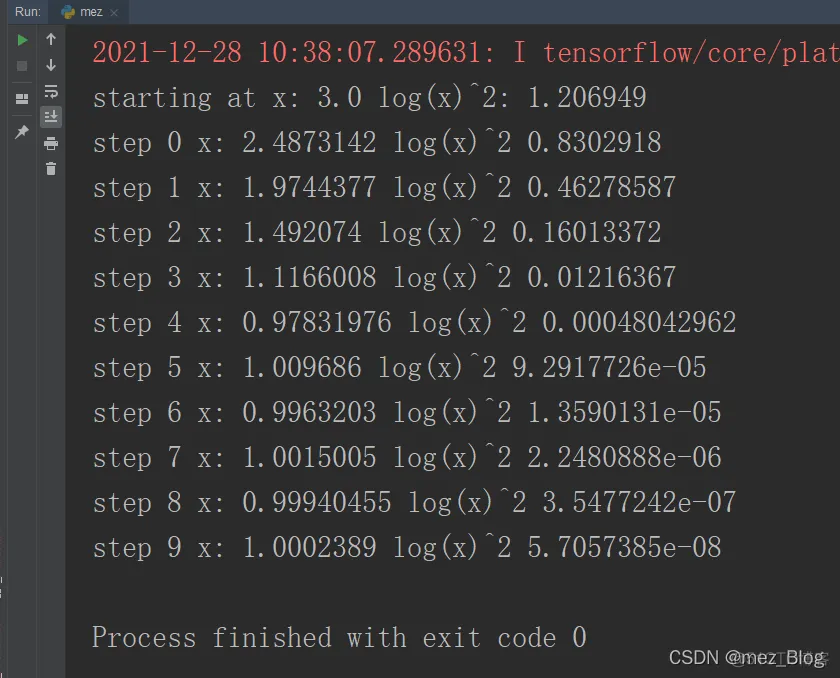
免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删