高阶累积量在信噪比盲估计中的MATLAB仿真应用

1.软件版本

matlab2013b

2.系统描述

所谓高阶统计量，通常是指信号的高阶矩，高阶累积量等信号统计信息的统称。在这些高阶统计量中，高阶累积量具有十分重要的重用，不同阶数的累积量可以反映出信号的不同特征，因此高阶累积量往往应用在信号分类，信号调制方式识别等领域。高阶累积量中的二阶累积量和四阶累积量可以有效抑制高斯白噪声的干扰，且对相位偏移具有一定的容错能力，其数学表达式为：

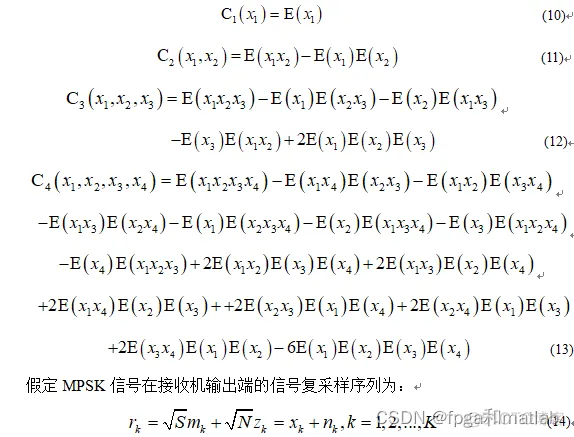
MPSK发送信号为相互独立的同分布序列，则：

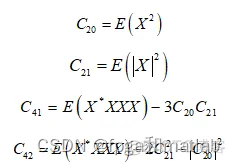
由于噪声的四阶累积量恒为零，噪声与信号独立，因此可以接收信号的高阶累积量可以表示为：

3.部分源码

登录后复制

function [c21,c42]=func_csum(yy)N      = length(yy);sum_C21=0;sum_C42=0;
 for i = 1:100    C20=mean(yy.^2);    C21=mean(abs(yy).^2);    
 C41=mean((yy.^3).*conj(yy))-3*C20*C21;    C42=mean(abs(yy).^4)-abs(C20)^2-2*C21^2;    
 sum_C21=sum_C21+C21;    sum_C42=sum_C42+C42;  endc21=sum_C21/100;c42=sum_C42/100; 1.2.3.4.5.6.
 7.8.9.10.11.12.13.14.15.16.17.18.19.




登录后复制

clc;clear;close all;warning off;%MPSK调制%参数说明% y         输出序列% x         输入序列% fc        
载波频率% fs        采样频率% rc        码元速率% M         调制模式M=2，4，8x      = rand(1,200)>=0.5;fc     
= 16e6;fs     = 4*fc;rc     = 2e6;M      = 4;detafy = 0*pi/6;[y0,y_test] = func_MPSKgen(x,fc,fs,rc,M,detafy);
%%%通过信号子空间估计信噪比%通过高阶累积量估计信噪比SNR    = [0:0.5:20];R1     = zeros(size(SNR));R2     
= zeros(size(SNR));for sj = 1:length(SNR)    sj    y         = awgn(y0,SNR(sj),'measured');    
[c21,c42] = func_csum(y);%高阶累积量    SNRset1   = sqrt(abs(c42)/2)/(c21-0.965*sqrt(abs(c42)))+4;        
SNRset2   = func_snr_est(y);    R1(sj)    = SNRset1;    R2(sj)    
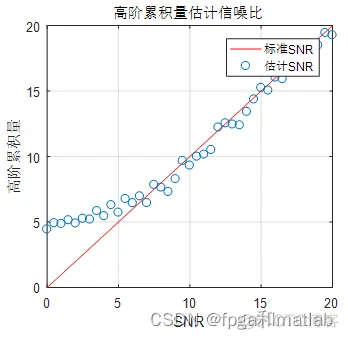
= SNRset2;end figure;subplot(121)plot(SNR,SNR,'r');hold onplot(SNR,R1,'o');grid onxlabel('SNR');
ylabel('高阶累积量');legend('标准SNR','估计SNR');title('高阶累积量估计信噪比');
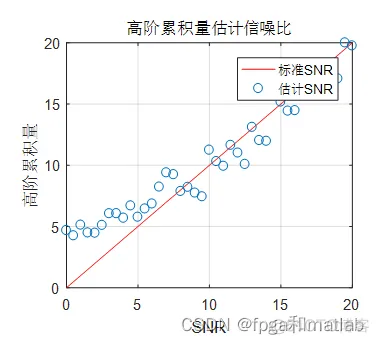
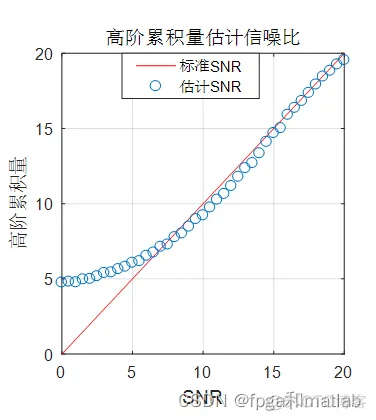
subplot(122)plot(SNR,SNR,'r');hold onplot(SNR,R2,'o');grid onxlabel('SNR');
ylabel('高阶累积量');legend('标准SNR','估计SNR');title('信号子空间估计信噪比');
sqrt(sum((SNR-R1).^2)/length(R1))sqrt(sum((SNR-R2).^2)/length(R2)) 1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16
.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.40.41.42.43.44.45.46.47.48.49.50.51
.52.53.54.55.56.57.58.59.60.61.62.63.64.65.66.67.68.69.70.71.72.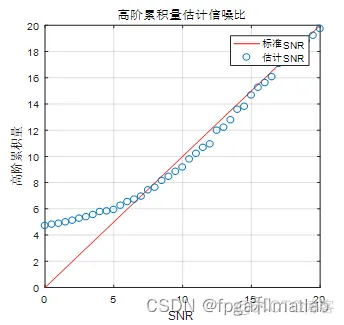

4.仿真结论

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删