产品
1.算法仿真效果
matlab2022a仿真结果如下: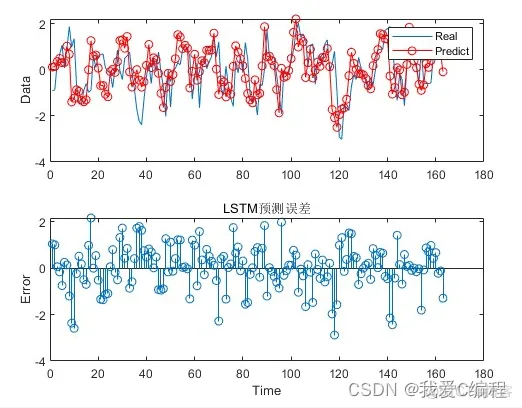
2.算法涉及理论知识概要
长短期记忆网络(LSTM,Long Short-Term Memory)是一种时间循环神经网络,是为了解决一般的RNN(循环神经网络)存在的长期依赖问题而专门设计出来的,所有的RNN都具有一种重复神经网络模块的链式形式。在标准RNN中,这个重复的结构模块只有一个非常简单的结构,例如一个tanh层。
长短期记忆网络(Long-Short Term Memory,LSTM)论文首次发表于1997年。由于独特的设计结构,LSTM适合于处理和预测时间序列中间隔和延
迟非常长的重要事件。LSTM的表现通常比时间递归神经网络及隐马尔科夫模型(HMM)更好,比如用在不分段连续手写识别上。2009年,用LSTM构建
的人工神经网络模型赢得过ICDAR手写识别比赛冠军。LSTM还普遍用于自主语音识别,2013年运用TIMIT自然演讲数据库达成17.7%错误率的纪录。作
为非线性模型,LSTM可作为复杂的非线性单元用于构造更大型深度神经网络。
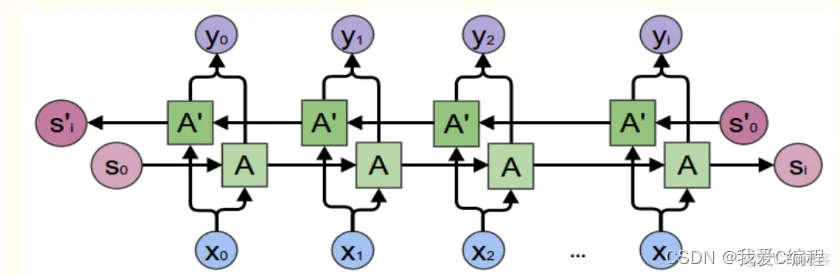
LSTM是一种含有LSTM区块(blocks)或其他的一种类神经网络,文献或其他资料中LSTM区块可能被描述成智能网络单元,因为它可以记忆不定时间
长度的数值,区块中有一个gate能够决定input是否重要到能被记住及能不能被输出output。图1底下是四个S函数单元,最左边函数依情况可能成为
区块的input,右边三个会经过gate决定input是否能传入区块,左边第二个为input gate,如果这里产出近似于零,将把这里的值挡住,不会进到
下一层。左边第三个是forget gate,当这产生值近似于零,将把区块里记住的值忘掉。第四个也就是最右边的input为output gate,他可以决定
在区块记忆中的input是否能输出 。LSTM有很多个版本,其中一个重要的版本是GRU(Gated Recurrent Unit),根据谷歌的测试表明,LSTM中
最重要的是Forget gate,其次是Input gate,最次是Output gate。
电力系统负荷预测是指充分考虑历史的系统负荷、经济状况、气象条件和社会事件等因素的影响,对未来一段时间的系统负荷做出预测。负荷预测是电
力系统规划与调度的一项重要内容。短期(两周以内)预测是电网内部机组启停、调度和运营计划制定的基础;中期(未来数月)预测可为保障企业生
产和社会生活用电,合理安排电网的运营与检修决策提供支持;长期(未来数年)预测可为电网改造、扩建等计划的制定提供参考,以提高电力系统的
经济效益和社会效益。复杂多变的气象条件和社会事件等不确定因素都会对电力系统负荷造成一定的影响,使得传统负荷预测模型的应用存在一定的局
限性。同时,随着电力系统负荷结构的多元化,也使得模型应用的效果有所降低,因此电力系统负荷预测问题亟待进一步研究。
电力负荷预测是一种典型的时间序列回归预测任务。电力负荷预测是保证电力供需平衡的基础,并为电网、电源的规划建设以及电网企业、电网使用者的
经营决策提供信息和依据。负荷预测分为长期、中期、短期和超短期负荷预测,预测对象包括系统负荷和母线负荷,由电网企业负责组织编制。大用户应
根据有关规定,按时报送其主要接装容量和年、月用电量预测及日用电负荷变化过程。
传统RNN网络由于结构存在固有缺陷,在参数更新时会存在梯度消失以及梯度爆炸的问题,导致长距离的历史信息丢失,进一步造成网络极难收敛,无法
训练出理想的模型。LSTM作为一种改进的循环神经网络,在原有网络结构的基础上加入了细胞状态(cell state)的结构来控制全局信息的传输,并通
过遗忘门,输入门,输出门三种门控单元控制细胞状态信息值的更新。LSTM在极大程度上缓解了传统RNN模型存在的长期依赖问题,减少了长距离历史
信息的丢失,输出的预测结果更准确 。
LSTM通过以下公式进行更新权值矩阵和偏置参数等网络信息:
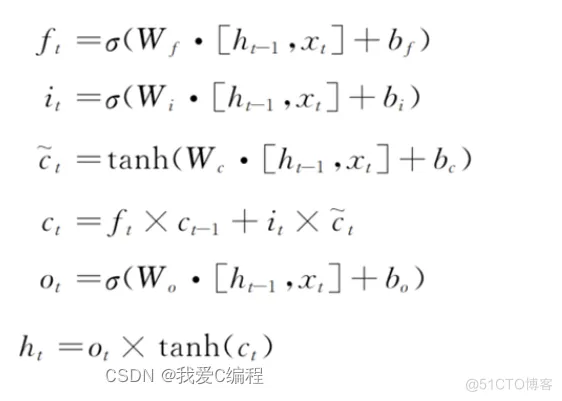
3.MATLAB核心程序
numResponses = 1;
numHiddenUnits = 128;
layers = [ sequenceInputLayer(numFeatures)
lstmLayer(numHiddenUnits)
dropoutLayer(0.12)
lstmLayer(2*numHiddenUnits)
dropoutLayer(0.12)
fullyConnectedLayer(numResponses)
regressionLayer];
options = trainingOptions('adam', ...
'MaxEpochs',200, ...
'GradientThreshold',1, ...
'InitialLearnRate',0.005, ...
'LearnRateSchedule','piecewise', ...
'LearnRateDropPeriod',125, ...
'LearnRateDropFactor',0.2, ...
'Verbose',0, ...
'Plots','training-progress');
net = trainNetwork(XTrain,YTrain,layers,options);
Xall = wdata_origin(:, 1:end-1)';
Yall = wdata_origin(:, end)';
YPred = predict(net,Xall,'MiniBatchSize',1);
rmse = mean((YPred(:)-Yall(:)).^2)
figure
subplot(211)
plot(data_x(1:length(Yall)), Yall)
hold on
plot(data_x(1:length(Yall)),YPred,'r-o')
legend(["Real" "Predict"])
ylabel("Data")
subplot(212)
stem(data_x(1:length(Yall)), YPred - Yall)
xlabel("Time")
ylabel("Error")
title('LSTM预测误差');
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删