PTS、SLM、Filter降低PAPR方法的Matlab性能仿真

1.算法仿真效果

matlab2022a仿真结果如下：

2.算法涉及理论知识概要

正交频分复用(OFDM)是长期演进的4G蜂窝网络标准中采用的调制技术。但是，OFDM具有较强的带外辐射和较高的旁瓣，对频谱的感知精度低下。未来的无线标准需要为下一代移动系统提出具有高传输数据速率和高频谱利用率的新调制技术。带有偏移正交幅度调制(OQAM)的滤波器组多载波调制(FBMC)作为未来第五代移动通信标准中的主要候选，已经引起了人们的关注。

登录后复制

FBMC-OQAM是一种多载波技术，通过基于快速傅里叶逆变换/快速傅里叶变换的滤波器组和OQAM符号，能够以两倍FBMC/QAM的符号速率将实数
符号载入子载波，因此具有较高的频谱效率。利用较小旁瓣的滤波器减小了载波频移，缓解了其对OFDM传输的影响，可以使频谱带外泄露特别低。
因为FBMC-OQAM系统中没有插入循环前缀，所以具有高传输数据速率和高频谱利用率。然而，FBMC-OQAM与OFDM都是多载波调制技术，在符号传
输过程中，由于多个子信道传输信号的叠加会产生较大的峰值，从而引起较高的峰均比(PAPR)。高PAPR导致非线性功率放大器中FBMC-OQAM性能
的严重劣化，所以降低FBMC-OQAM系统的PAPR是下一代通信技术的一个主要问题。一般地，PAPR降低技术可以大致分为两大类——有失真技术和无
失真技术。有失真技术包含压扩法技术(星座扩展法)和限幅类技术(消峰法)，无失真技术包含编码类技术(分组编码)和概率类技术。概率类的解决
方案如选择性映射(SLM)和部分传输序列(PTS)方案，主要是降低信号中高峰值出现的概率，而不是减少最大信号的幅度[4]。它们具有相对较低的
复杂度，在边带信息恢复时不会影响误码率，因而更具优势。

2.1pts

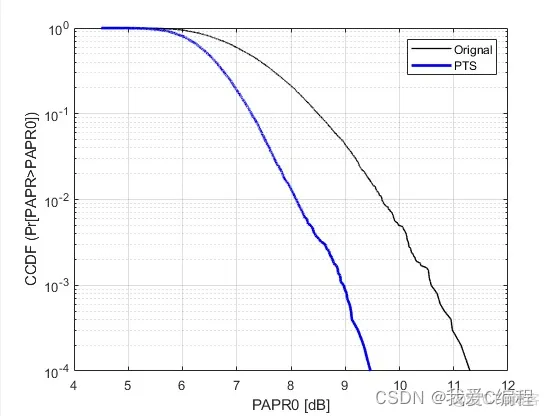
部分传输序列(Partial Transmit Sequence , PTS)由于其不受载波数量限制，并且能够有效的，无失真的降低OFDM信号峰均比，而受到广泛关注。部分传输序列算法(PTS)最初是由S.H.Muller和J.B.Huber于1997年提出。PTS算法的核心思想是将具有N个符号的输入序列按照一定的分割方式分割成V个子数据块，并且保持每个子数据块仍含有N个符号。然后对V个子数据块进行相位加权与合并处理，选择具有最小PAPR的一组符号进行传输，达到降低OFDM信号PAPR的目的。传统的PTS算法理论比较多，现成的资料也比较多，这里就不多做介绍了，通过仿真，对比PTS和没有PTS下。目前OFDM的PAPR主要算法有信号预畸变，信号扰码，编码三个方向来解决。

登录后复制

在本课题中，我们将在传统PTS算法基础上引入了TR的思路到改进后的PTS算法中，引入的意义为：先预留出若干子载波来加载削峰信号，然后利用
优化过的PTS算法对OFDM符号的PAPR进行抑制，之后再利用改进的TR算法对符号的PAPR进行进一步的抑制。整个算法的流程如下所示：

步骤一：加入门限，降低PTS算法的复杂度（但是这样会降低性能）

当满足要求：

算法就停止搜索，这样的话，就降低的算法的复杂度，但是会影响性能。

步骤二：加入限幅的方法

通过这个方法，可以在步骤一的基础上，提高性能，使其在复杂度降低的前提下，保存系统的性能不变。

2.2SLM
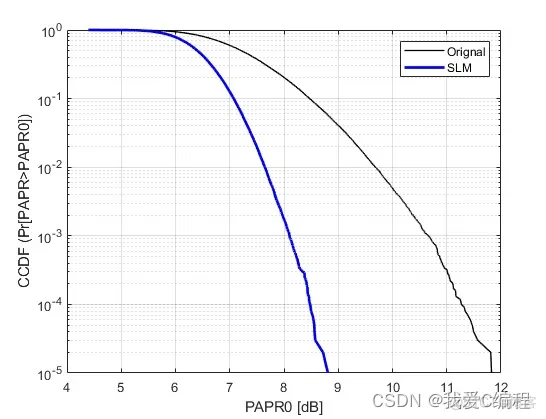
slm算法就是对QAM信号乘以U组相位因子序列，再进行ifft得到 U组ofdm信号，选择papr最小的那一组进行发送。

因为对于ofdm信号而言，高PAPR出现的概率很小，一般1000个ofdm信号只会有个位数papr过高的值。那SLM方法对同一个QAM信号乘以N组相位后得到U个ofdm信号，从中选择PAPR最小的进行发送，就用概率的方法将高PAPR的ofdm信号滤出在外。

2.3 Filter

for nIter=1:ITERATE_NUM

% Clipping

x_tmp = x(Signal_Power>CRMean_Power);
x_tmp = sqrt(CRMean_Power)x_tmp./abs(x_tmp);
x(Signal_Power>CRMean_Power) = x_tmp;

登录后复制

    % Filtering
    XX = fft(x,[],2);
    XX(K/2+(1:N-K)) = zeros(1,N-K);
    x = ifft(XX,[],2); 
    
    % PAPR Compute
    Signal_Power = abs(x.^2);
    Peak_Power   = max(Signal_Power,[],2);
    Mean_Power   = mean(Signal_Power,2);
    PAPR_RCF(nIter,nSymbol) = 10*log10(Peak_Power./Mean_Power);
end

3.MATLAB核心程序

登录后复制

N = 4;                                                                      
QPSK_Set  = [1 -1 j -j];
Phase_Set = [1 -1];
MAX_SYMBOLS  = 1e5;
PAPR_Orignal = zeros(1,MAX_SYMBOLS);
PAPR_SLM     = zeros(1,MAX_SYMBOLS);
X     = zeros(N,K);
Index = zeros(N,K);
for nSymbol=1:MAX_SYMBOLS
    Index(1,:)   = floor(length(QPSK_Set)*rand(1,K))+1;
    Index(2:N,:) = floor(length(Phase_Set)*rand(N-1,K))+1;
    
    X(1,:) = QPSK_Set(Index(1,:));                                                                    
......................................................
    x = ifft(X,[],2);                                                       
    Signal_Power = abs(x.^2);
    Peak_Power   = max(Signal_Power,[],2);
    Mean_Power   = mean(Signal_Power,2);
    
    PAPR_temp = 10*log10(Peak_Power./Mean_Power);
    PAPR_Orignal(nSymbol) = PAPR_temp(1);
    PAPR_SLM(nSymbol)     = min(PAPR_temp);
end
[cdf1, PAPR1] = ecdf(PAPR_Orignal);
[cdf2, PAPR2] = ecdf(PAPR_SLM);
 
 
figure;
semilogy(PAPR1,1-cdf1,'-k','LineWidth',1)
hold on
semilogy(PAPR2,1-cdf2,'-b','LineWidth',2)
legend('Orignal','SLM')
xlabel('PAPR0 [dB]');
ylabel('CCDF (Pr[PAPR>PAPR0])');
grid on

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删