ANSYS/LS-DYNA助力：镁合金无人机起落架跌落分析

摘    要：

【目的】铝合金起落架在使用过程中，由于其具有质量高的特点会给无人机带来很多不必要的动能损耗。

【方法】课题组以某型号的植保无人机为研究对象，通过制作材料的平替和优化结构设计，使其达到使用要求。对无人机起落架进行UG设计建模以及ANSYS有限元分析，得到起落架对应的应力云图和变形云图。材料平替过程中，质量由铝合金的0.86kg下降到了稀土镁合金的0.68 kg，质量降低0.18 kg。

【结果】通过LS-DYNA跌落仿真结果可知，最大变形为7.416 mm，最大应力为196.46 MPa，低于材料屈服强度极限，满足强度要求，且跌落速度对起落架的变形影响更大，可以为同类型产品设计提供思路。

【结论】

1）通过替换镁合金材料作为起落架制作材料，对比铝合金质量减轻了20.9%。

2）通过建立滑橇式起落架落震仿真模型，并通过输入合理的材料应力-应变曲线符合起落架着陆过程中的实际情况，准确模拟了起落架的落震试验过程

3）通过仿真计算分析，发现其速度对跌落过程中起落架的变形影响远大于起落架承担载荷多少的影响。研究结果对后续起落架的设计和优化具有较大的工程实际应用价值。

关键词：无人机;起落架;ANSYS;LS-DYNA跌落分析;

0 引言

我国是一个农业大国，随着科技的发展和农业科技水平的提高[1]，越来越多的科技产品被投入到农业生产中。植保类无人机的大量使用便是典型代表，相较于传统的手工喷药方式，大大提高了药物喷洒的工作效率。

植保无人机起落架，在无人机停放降落中扮演着十分重要的角色。无人机停放时，由起落架给予一个稳定可靠的支撑；在无人机降落时，可以给予无人机一个良好的缓冲作用[2]，以防止机身过载带来的机体损坏。尤其是在无人机降落时，地面对无人机会有一个很大的刚性冲击，其冲击大小与无人机的质量和速度有很大的关系。目前，市场上广泛使用的起落架制作材料为铝合金，但是铝合金起落架在使用过程中由于其具有质量高的特点会给无人机带来很多不必要的动能损耗。因此，设计一款轻量化的起落架来降低起落架质量和提高飞行时间，从而达到增加无人机的续航时间的目的，显得很有必要。我国是镁资源生产大国，近年来对镁合金的研究越来越深入，由于其很高的比强度和比刚度被广泛应用于汽车、航空航天等工业领域中[3,4]。使用镁合金代替传统铝合金材料作为起落架的制作材料，将会有很大的研究价值和应用市场。

课题组以某型号的植保无人机起落架为研究对象，通过有限元软件ANSYS对起落架在满载工况下进行静力分析，验证了镁合金作为起落架制作材料的基本可行性。并对其不同载荷和跌落速度进行跌落仿真分析，进一步验证了其作为起落架制作材料的可行性[5,6]。

1 无人机起落架的模型建立

1.1 起落架结构分析

某小型植保无人机满载质量为33 kg，降落时允许最大下沉速度为3 m/s，起落架要有足够的强度满足此要求。选择的材料为稀土镁合金，材料参数如表1所示。

表1 材料及参数

1.2 网格的划分

网格划分属于有限元分析前处理阶段中的必不可少的一环，并且也是十分重要的一个阶段，比如网格尺寸大小的确定对计算的精度影响较大。本研究采用四面体主导的方法进行网格划分，单元尺寸为3mm，网格节点数为115 995，单元格数量为60 211，模型网格划分图如图1所示。

图1 网格划分图

2 起落架跌落仿真

网格划分和部分设置与上文一致，在UG中新建一个平面为地面，在材料属性中定义地面为混凝土，定义刚度行为为刚性。

本文选用ANSYS/LS-DYNA模块作为此次仿真的模拟平台，此平台结合了ANSYS的强大前后处理功能和LS-DYNA求解器的强大分析能力[7],L S-D Y N A通过瞬态动力学分析结构动力学响应，ANSYS/LS-DYNA显示时间积分采用中心差分法，即n个时间步结束后加速度的计算和LS-DYNA中的时间步长计算分别为：

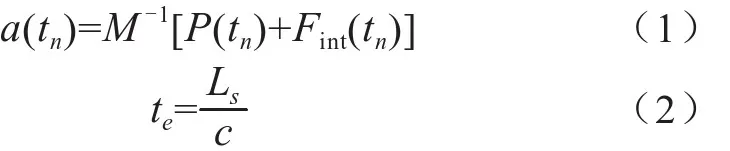
式中，M为质量矩阵；P为第n个时间步内所施加的节点外力向量；Fint为tn时刻的内力矢量；te为最小时间步长；Ls为单元特征长度；c为冲击波在材料中的传递速度[8]。

3 双撬水平跌落分析

跌落分析完成后，可以得到双撬水平着陆时不同载荷、不同速度对应的应力变形云图，9次跌落计算分析参数如表2所示[9,10]。

表2 起落架着陆参数

以满载33 kg，跌落速度为3 m/s为例，其应力云图、变形云图分别如图2、图3所示。

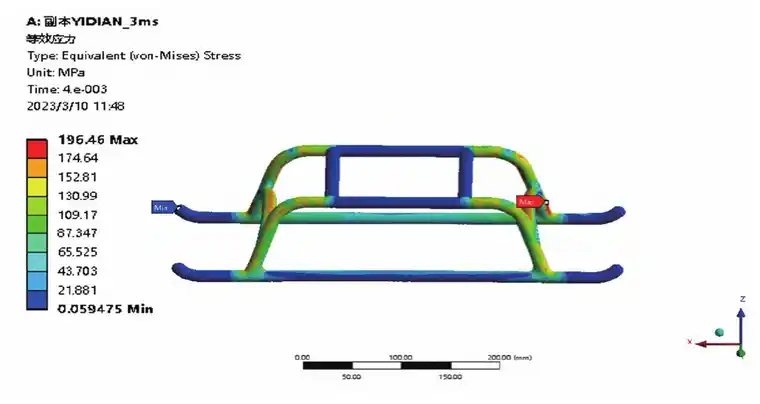
图2 3 m/s满载应力云图

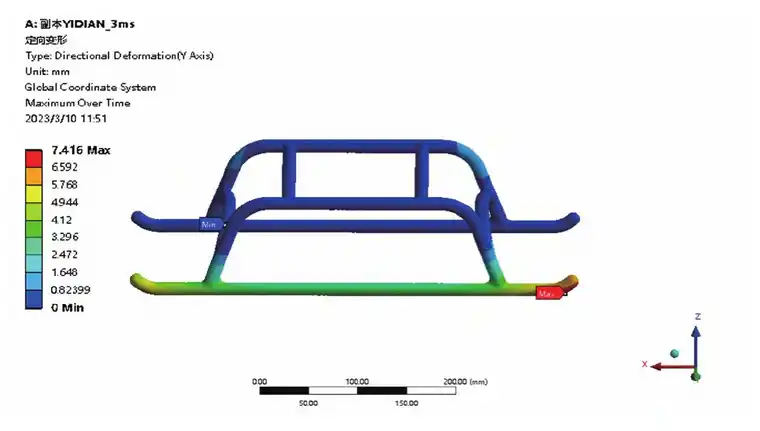
图3 3 m/s满载变形云图

由图2可知，在跌落速度为3 m/s时，最大应力都集中在起落架两拱形支架与两侧支架的下方位置，此时对应的最大应力为196.46 MPa；由图3可知，最大变形为起落架着陆时接触地面滑橇的远端处，此时起落架最大变形为7.416 mm。其最大的应力仍在材料的许用范围内，满足设计强度要求。因此可以进一步证明镁合金材料用于无人机起落架的可行性。

查看跌落过程中的变形情况，以满载33 kg、速度3 m/s跌落情况为例，其满载Y向位移图如图4所示。

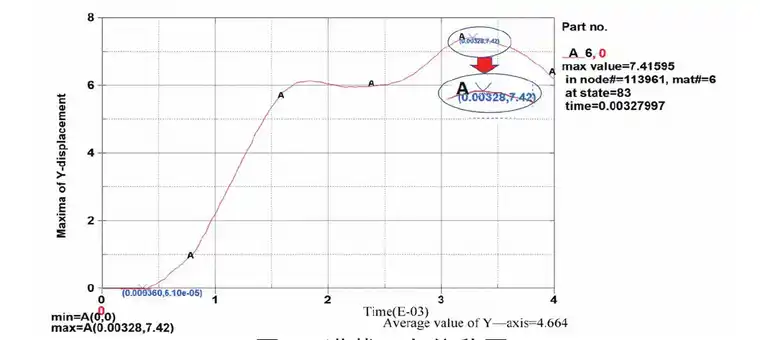
图4 满载Y向位移图

由图4可知，在0.000 4 s时，起落架两侧滑橇与地面开始接触，此后变形逐渐增大。在0.003 28 s时，跌落变形达到最大值，此时对应的最大位移为7.416mm。此后，起落架开始回弹，变形逐渐减小。

将以上9种工况分析计算完成，其变形数据如表3所示。

由表3可知，工况9下，起落架的变形最大，达到了7.416 mm。

为进一步得出跌落过程中载荷与跌落速度对起落架的影响，对上述9种工况数据进行整理拟合：当跌落速度一定时，以1 m/s为例，不同载荷对起落架变形的影响如图5所示；当载荷一定时，以18 kg为例，不同跌落速度对起落架变形的影响如图6所示。

由图5可知，当跌落速度不变时，以跌落速度1m/s为例。当载荷为18 kg时，起落架两侧滑橇的最大变形为1.868 mm；当跌落载荷增加到25.5 kg时，起落架的最大变形为2.015 mm，较载荷18 kg时增加了2.015-1.868=0.147 mm；当跌落载荷达到33 kg时，起落架的最大变形为2.119 mm，较25.5 kg时增加了2.119-2.015=0.104 mm。对比发现，当跌落的载荷约为倍数增加时，起落架的变形也会有较小浮动的增加，其增长率约为（0.147+0.104）/1.868=13%。

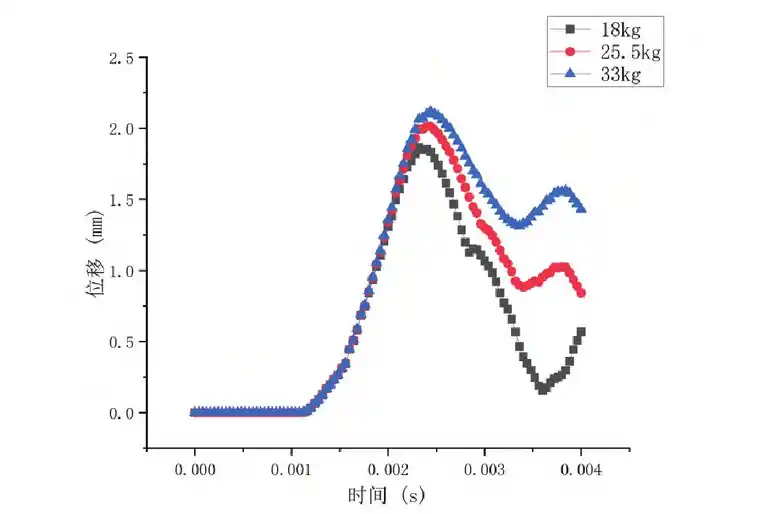
图5 1 m/s不同载荷位移-时间图

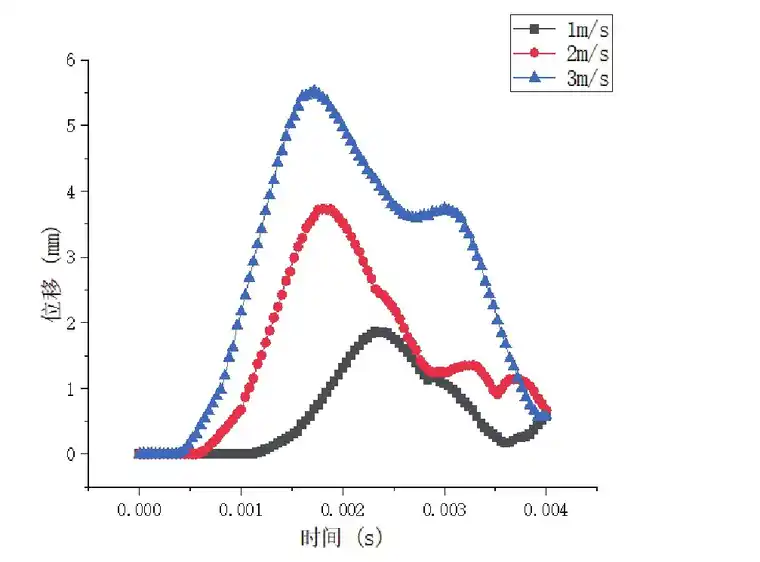
图6 18 kg不同速度位移-时间图

由图6可知，当载荷不变时，以载荷18 kg为例。当速度为1 m/s时，最大变形为1.868 mm；当起落架跌落速度提升到2 m/s时，起落架的最大变形为3.73 mm，较速度1 m/s时增加了3.73-1.868=1.862m m；当起落架跌落速度达到3 m/s时，最大变形达到了5.521 mm，较速度2 m/s增加了5.521-3.73=1.791 mm。对比发现，跌落的速度呈倍数增加时起落架的变形几乎也呈倍数增长，其增长率约为1.791/1.868=96%。由此可知，跌落速度对起落架两侧滑橇的变形影响很大，几乎呈倍数增长。

4 结论

课题组以某型号无人机起落架为研究对象，利用ANSYS对起落架进行了不同高度和载荷下的跌落分析。对比分析后得到以下结论：

表3 不同工况下变形数据

1）通过替换镁合金材料作为起落架制作材料，对比铝合金质量减轻了20.9%。

2）通过建立滑橇式起落架落震仿真模型，并通过输入合理的材料应力-应变曲线符合起落架着陆过程中的实际情况，准确模拟了起落架的落震试验过程。

3）通过仿真计算分析，发现其速度对跌落过程中起落架的变形影响远大于起落架承担载荷多少的影响。研究结果对后续起落架的设计和优化具有较大的工程实际应用价值。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删