ALE法在盛油容器跌落模拟中的创新应用

1 背景介绍      

LS-DYNA程序是功能齐全的几何非线性、材料非线性和接触非线性程序。它以Lagrange算法为主，兼有ALE和Euler算法；以显式求解为主，兼有隐式求解功能;以结构分析为主，兼有热分析、流体-结构耦合功。本案例以ALE算法，分析了油箱跌落问题。首先简述下ALE算的发展：

ALE是Arbitrary Lagrangian-Eulerian的缩写，称为任意拉格朗日欧拉法。该概念最早由Nor和Hirt等人以Coupled Eulerian-Lagrangian描述的名称提出的，并引入到有限元法中。最早是为了满足核反应堆结构安全分析中的非线性数值模拟技术的需要。ALE有限元法最初的工作是解决非黏性可压流体。Hughes等人研究了不可压粘性液体流动问题和带有自由液面液体流动问题，并首先建立了ALE描述的一般运动学理论Belytschko等人数值模拟了液体内部液泡的膨胀过程，给出了一种既灵活方便又简单易行的网格更新方案；边界上的单元结点采用拉格朗日描述，内部的网格结点速度可根据边界上的结点速度线性插值得到。其后，Liu和Huerta等人发展了ALE有限元的一般理论框架，推导了相应的有限元公式，研究了瞬时ALE有限元法的计算机程序设计问题并应用于贮腔类三维液体动力学问题研究。

这种方法兼具Lagrange方法和Euler方法二者的特长，即首先在结构边界运动的处理上，它引进了Lagrange方法的特点，因此能够有效地跟踪物质结构边界的运动；其次，在内部网格的划分上，它吸收了Euler的长处，使内部网格单元独立于物质实体的存在，但它又不完全和Euler网格相同，网格可以根据定义的参数在求解过程中适当调整位置，使得网格不致出现严重的畸变。这种方法在分析大变形问题时非常有利。使用这种方法时网格与网格之间的物质也是可以流动的。 目前，ALE有限元法已被广泛应用于解决大范围移动边界(或接触面)问题，特别是在液体大幅晃动问题、流固耦合、加工成型、接触、大变形等领域获得极大成功。

2 模型描述

模型简化：为了满足硬件计算资源的要求，在不影响计算效果条件下对模型做了适当简化。主要研究了液面在Z向的位移变化，所以在厚度方向采用减薄处理，用3排实体单元描。

地面简化为刚体，其余结构的单元采用六面体单元，模型总单元数26568 。结构如下图：

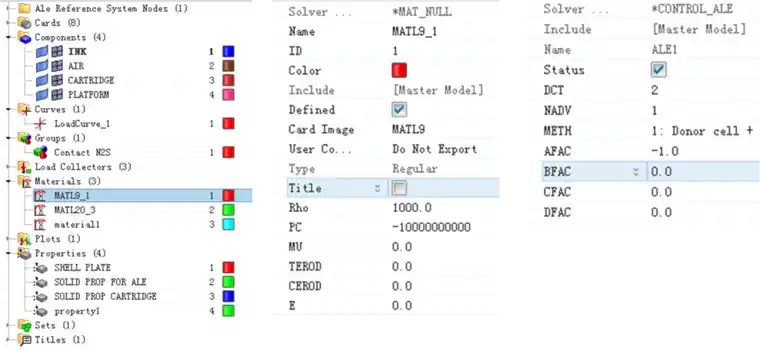
3 计算结果

求解设置，cpu=4，最小步长=1e-7，总时长0.01s，初速度=1m/s。结果如下图：

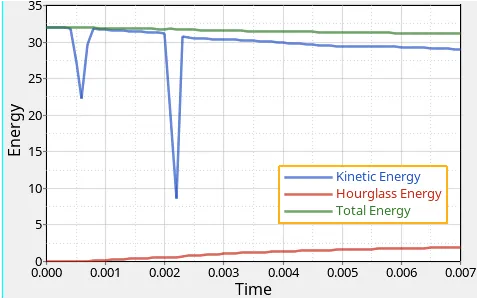
4 结论

ALE这种方法兼具Lagrange方法和Euler方法二者的特长，即首先在结构边界运动的处理上，它引进了Lagrange方法的特点，因此能够有效地跟踪物质结构边界的运动；其次，在内部网格的划分上，它吸收了Euler的长处，使内部网格单元独立于物质实体的存在，但它又不完全和Euler网格相同，网格可以根据定义的参数在求解过程中适当调整位置，使得网格不致出现严重的畸变。

ALE有限元法广泛应用于大范围移动边界问题，特别是在液体大幅晃动问题、流固耦合.

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删