平头弹冲击双层靶：LS-DYNA数值模拟新视角

1、引言

在军事应用和民用防护中，穿甲问题扮演着重要角色，其中平头弹穿甲金属板问题十分具有代表性。穿甲实验是是研究这类问题最重要、最基本的研究方法，但成本高，理论分析有一定的适用范围，而数值模拟技术以其在经济性和效益性方面的优势，日益成为研究穿甲问题不可或缺的研究手段。随着实验技术的提高、计算机的发展和相关理论的提出，平头弹对单层靶破坏模式得到了较充分的认识。近年来，双层靶的穿甲破坏模式研究受到广泛关注，但还远不及单层靶，对双层靶研究的深度和宽度也很有限。目前主要手段为实验研究和数值模拟，缺乏失效模式的理论模型。双层靶板结构形式分为接触式和间隙式，本文将通过ANSYS/LS-DYNA来论证平头弹穿透间隙式双层靶的失效模式。

2、有限元分析

2.1 弹靶材料本构模型

在数值模拟中，靶板采用采用Johnson-Cook（JC）强度模型和累积损伤失效模型来描述靶材的力学性能，JC本构模型常用于模拟金属材料从低应变率到高应变率下的动态行为，该模型利用变量乘积关系分别描述应变、应变率、温度和损伤因子的影响，具体形式为：  

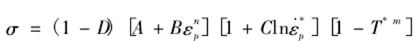
式中参数具体含义请自查文献，本文不加赘述。

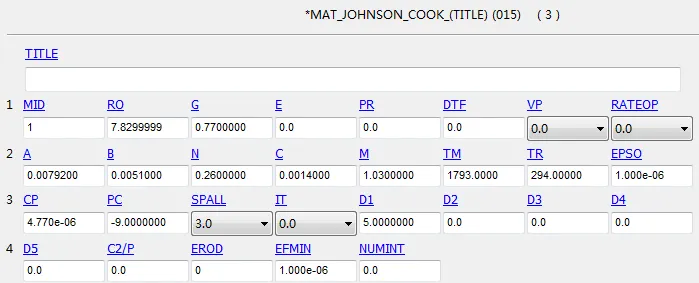
在本文数值模拟中，靶板采用Johnson-Cook（JC）强度模型和累积损伤失效模型来描述靶材的力学性能，弹体材料模型服从Von Mise屈服准侧，采用双线等向强化模型。本文中靶板材料的具体数值如下图所示：

为简化计算，弹体材料模型选用LS-DYNA中的20号刚体材料本构模型。

2.2弹靶有限元模型

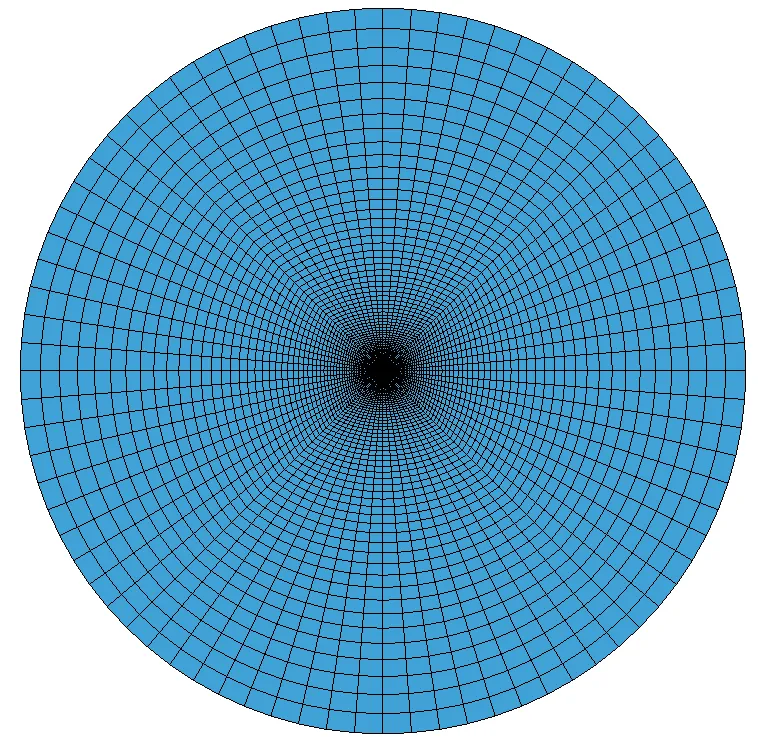
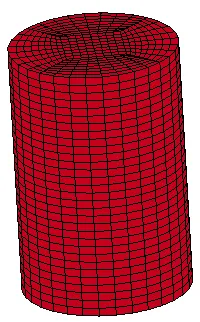
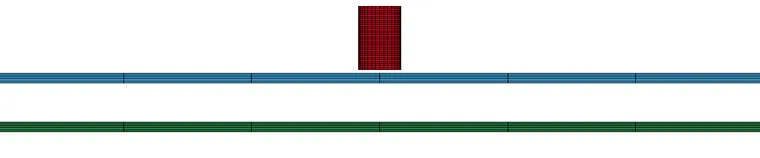
本文所采用双层靶的有限元模型如下图所示，靶体直径为100，每层的厚度为0.5，层间间隙为2.3；弹体为圆柱形，直径为2.8，弹长4。弹体和靶板网格均用Lagrange映射网格方法划分为六面体单元，为提高计算精度，在靶体圆心处（即弹体冲击位置）及附近区域的网格进行加密。

2.3 其他求解条件设置

求解之前，需要设置模型的边界条件、冲击速度等，具体内容参考下图。

由于本模型为对称模型，计算中可进一步简化为1/4模型进行计算，在对称边界上施加对称约束，在靶板边界处施加非反射边界，以此来模拟无限大靶板。

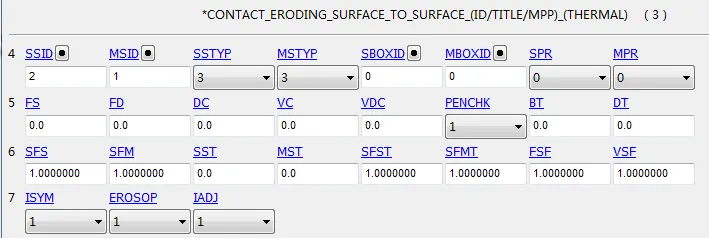
弹靶之间采用如下图所示的三维面对面侵蚀接触算法

除此之外，还要设置模型的终止计算时间以及结果输出的时间间隔。

模型设置完成之后即可导出K文件，并利用ANSYS中的LS-DYNA求解器进行求解。

3、数值结果分析

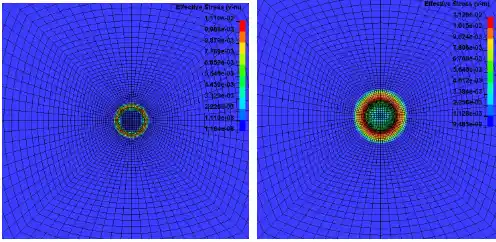
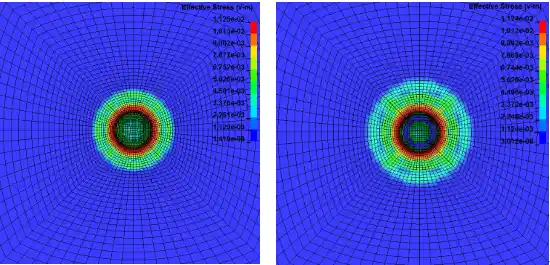
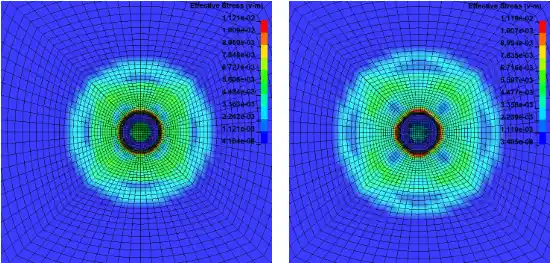
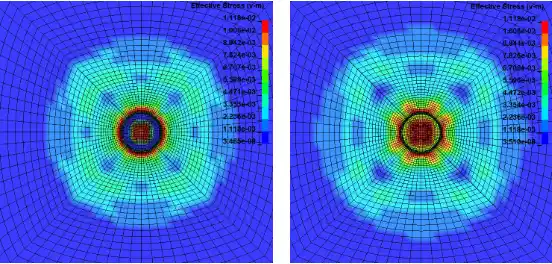
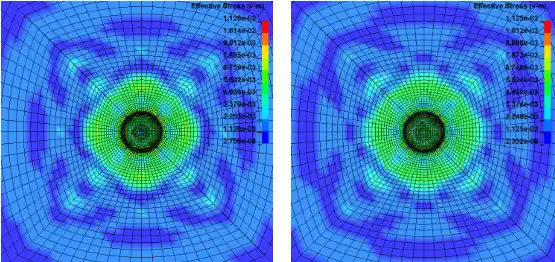
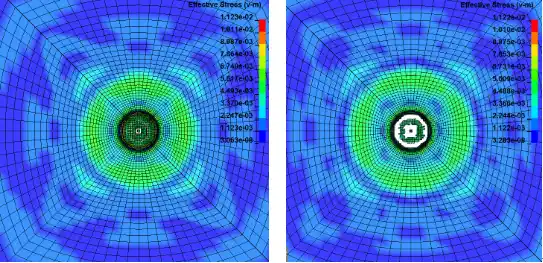
以上为双层靶板受平弹冲击后米塞斯应力随时间的变化展示。可以看出，顶层靶板首先被弹体冲击发生击穿现象，应力响应随时间向周围扩展，并且与平弹底部接触的靶板单元发生整体脱落进而作用到底层靶板，底层靶板首先因受到脱落碎屑的冲击而产生应力，但是这种冲击载荷较小未使靶板失效，随后平弹的继续冲击作用于底层靶板，最终导致靶板发生击穿。本模型能够较为准确地模拟出平弹冲击靶板的真实效果，能够为相关内容提供思路和参考。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删