【问题描述】
在下图中,横梁ACB的变形可以忽略不计(即ACB为刚体)。钢杆AD的横截面积为100平方毫米,长度为330毫米,弹性模量为200Gpa,线胀系数为12.5*10(-6);铜杆BE的相应数据分别为:面积200平方毫米,长度220毫米,弹性模量100GPa,线胀系数为16.5*10(-6)。如果温度升高30度,试求两杆的轴力。

【理论分析】
该问题来自于《材料力学》“轴向拉伸压缩”一章中的“温度应力”一节(P45)。(刘鸿文,《材料力学》,高等教育出版社,第四版)
设两根杆件的内力为基本未知数,根据热膨胀,计算两根杆件的伸长量与内力的关系,然后基于变形协调关系,得到内力的大小。
最后计算的结果是:

上述答案直接拷贝自原教材。
【仿真分析】
1. 这是一个热应力问题。但是并不需要使用耦合系统。直接使用静力学系统可以求解。
2. 对于材料设置,需要创建两种材料:钢和铜,并分别给定其弹性模量,泊松比和线胀系数。对于AB杆,则设置刚性很大(例如弹性模量是钢材的千万倍)的材料。
3.几何建模。分别创建三个线体,分别代表AB,AD和BE。对于AD和BE赋予矩形截面属性,保证其横截面积即可。AB就使用AD的横截面属性。
4.属性设置。分别设置三杆的材料属性。
5.划分网格。给定5毫米的单元长度划分。
6.连接。所有连接处均使用转动副连接。
7.分析设置。给定参考温度和实际温度。
8.后处理。在后处理中提取梁单元的内力。
【仿真过程】
1.打开ANSYS WORKBENCH14.5
2.创建项目流程图。
这里创建一个静力学分析系统。

3.创建两种材料,并设置其属性。
双击engineering data单元格,然后创建两种新材料,按照题目的数据设置其弹性模量和线胀系数。
修改默认钢材属性,得到本题中钢材的属性。

加入铜合金,并修改其属性,得到本题中铜的属性

创建一个新材料,其弹性模量是2E18,即弹性模量是钢材的千万倍,用于模拟刚体。

4. 创建几何模型。
双击geometry,进入到DM中,设置长度单位是毫米。
以A点为坐标原点,水平向右为X轴正方向,竖直向上为Y轴正方向,建立坐标系。则各点的坐标如下。
A(0,0),B(390,0),C(240,0),D(0,330),E(390,220).
在DM中依次创建这5个关键点。

从点创建线体。注意ACB要成为一个线体,而AD,BE则是另外的两个线体,最终得到三个线体。
得到3个线体

其几何图形是

创建两个截面:
AD杆,AB杆设置为10mm*10mm的截面;而BE杆设置10mm*20mm的截面。

将上述截面分别给予对应的线体。显示截面形状,得到的几何模型如下图

为便于后面的杆件识别,给这几根杆件重命名

退出DM.
5. 设置杆件的属性。
双击model,进入到mechnical中。
AB是刚体,没有热应变。

AD是钢材,有热应变。

BE是铜合金,有热应变。

6.创建连接关系。
在D处创建AD杆和地面之间的转动副。

在E处创建BE杆和地面之间的转动副。

在C处创建AB杆和地面之间的转动副。

在A处创建AB杆和AD杆之间的转动副。

在B处创建AB杆和BE杆之间的转动副。

创建的5个转动副结果如下图
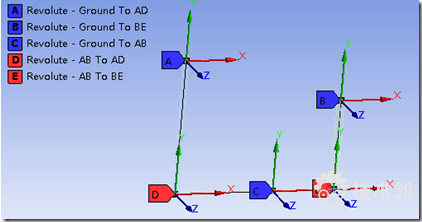
7. 划分网格。
设置5mm的单元长度,划分网格。

8. 设置温度载荷
对两根杆件AD,BE加载升温30度,达到52度。

9.求解。
10.后处理。
查看AD杆的轴力。

查看BE杆的轴力
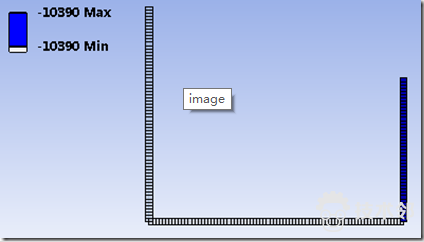
可见,
AD杆轴力的相对计算误差是:
(6.975-6.68)/6.68*100% = 4.4%
BE杆轴力的相对计算误差是:
(10.7-10.39)/10.7*100% = 2.9%.
计算精度可以接受。
实际上,可以减少AD杆和BE杆的网格划分份数,而增加AB杆的网格划分份数。从而得到更高精度的计算结果。
此外,对于AB杆,设定大的横截面积,会进一步提高计算精度。这应该是提高计算精度的较好的方法。
另外,如果能够直接设置AB为刚性物体的话,这是提高精度的最好的办法。
但是本文就不再赘述,更多的工作,留给朋友们去做吧。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删