引线键合超声换能器：经典案例分析

该示例问题模拟用于引线键合应用的超声换能器的电激励。该模型包括压电材料定义、预应力模态和谐波响应分析。

介绍

引线键合是使用精细金属（如金或铝）线在集成电路（IC）及其封装之间创建互连的最常用的工艺。在楔形键合中，施加超声波能量、压力和热量以形成键合；该方法避免了杂质的引入，并提供了材料选择的灵活性。对于较大直径的电线，频率通常在50-60kHz左右，而对于较小直径的电线来说，频率更高，高达200kHz。

换能器的设计包括检查与其纵向运动相关的固有频率。例如，几何形状的变化会影响设备的振动和电气特性。

在压电陶瓷中，施加的电压在材料中引起应变（位移），反之亦然，证明电场和结构场的耦合。压电陶瓷在拉伸时非常脆，因此需要预加载以使陶瓷在操作中保持压缩应力状态。

问题描述

下图显示了本例中使用的超声波换能器：

粘合工具由氧化铝制成，显示在最左侧。它通过小螺钉（未建模）连接到钛喇叭。喇叭连接到压电驱动器组件。驱动器组件由夹在铝前板和背板之间的压电环组成，通过提供预应力的钢螺栓连接在一起。传感器通过钢支架安装在机器上。

支架应放置在传感器的节点处，以获得最佳性能。在没有支架的情况下进行模态分析，并确定第一纵向模态。

如下图所示，轮廓范围为-1至1的z位移图提供了定位支架的适当位置：

建模

传感器的三维模型在ANSYS DesignModeler中创建，并在ANSYS Mechanical中进行网格化，如下图所示：

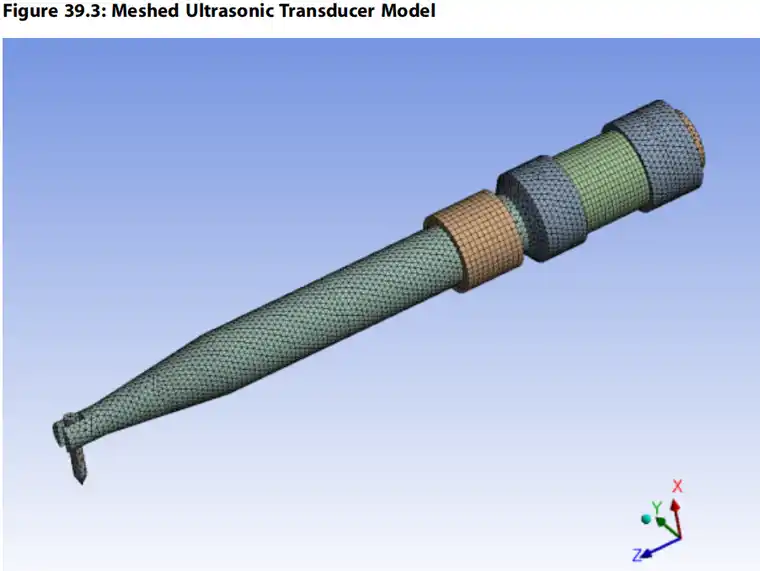
压电单元用SOLID226划分网格，其他部分用SOLID186和SOLID187单元划分网格。单元总数为67756，节点总数为115414。

耦合场单元SOLID226支持许多物理类型。在这种情况下，KEYOPT（1）＝1001指定压电行为。压电元件是正交各向异性的，因此每个压电环都假定具有交替z轴取向的z轴极化。

虽然铜端子位于压电环之间，但为了简单起见，这里省略了它们。其他细节和特征（如小螺钉或电线孔）也被省略，因为它们对整体响应没有影响。

这些部件通过接口上的共享节点进行连接。虽然接触单元可以用于压电分析，但在这种情况下，它们对于这种简单的几何结构是不必要的。

一个螺栓连接驱动器的顶板和底板，如下图所示：

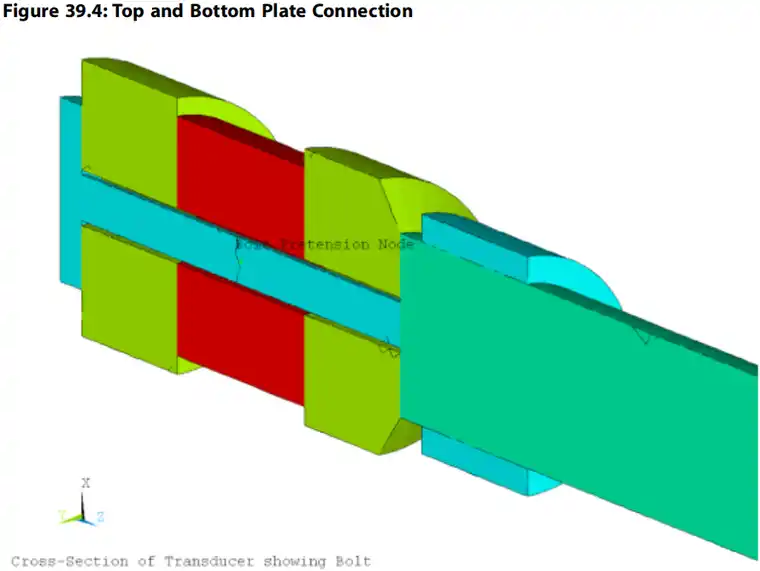
紧固件被分成两半，PRETS179预张紧单元将两半连接在一起。预紧力或调整量通过预紧节点控制。

材料属性

本问题中使用的结构材料性质如下：

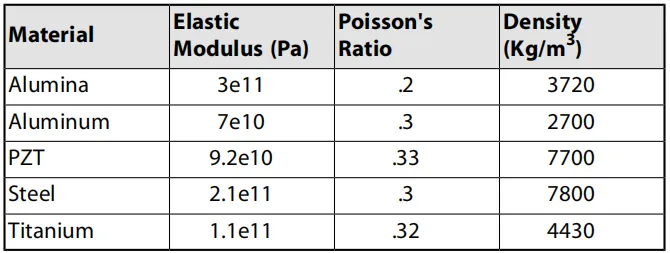
压电材料通常具有正交各向异性材料特性，尽管在本示例中假设各向同性材料，因为它们在参考文献中以这种方式定义。

压电材料特性如下：

该模型假设系统阻尼比为0.1%，因为超声换能器的阻尼很小。

边界条件和加载

结构和电气边界条件均施加。

结构边界条件

支架的外径在所有结构自由度上都受到约束。

进行静态分析以计算由于将螺栓紧固至驱动器组件而产生的预应力。对预紧节点施加50 N的预紧力。对于后续的动态分析，调整值更改为0.0。

尽管实际预紧力调整（夹持长度变化）为非零，但静态分析仅用于创建影响整体刚度矩阵的应力强化矩阵。在谐波响应分析中，所有载荷都是正弦施加的，因此施加预加载力或非零调整会产生谐波变化的螺栓载荷，这是不正确的。线性扰动分析中考虑了螺栓预紧力对驱动器刚度的影响，因此不需要在动态分析中进行实际调整。

压电耦合边界条件

每个压电环之间有一个电端子。环的极化方向相反，因此正负端子交替。

因为端子是等电位的，所以每个端子的所有电压自由度都是耦合的，在端子位置留下两个独立的电压自由度。一个电压指定为接地（电压为0）。

在模态分析中，正极端子不受约束。在谐波响应分析中，向正极端子施加相对于频率恒定的5V电压。

分析和求解控制

用线性摄动法进行预应力模态分析

在一端接地且螺栓预紧力为50N的情况下进行静态分析。然后使用线性摄动法和Block Lanczos特征求解器进行预应力模态分析，

其中需要前40个模态。螺栓调整更改为零。

预应力全谐波响应分析

首先进行上述静态分析。使用完整方法进行的预应力谐波响应分析用于计算57和60 kHz之间的频率响应（30个子步）。

在该谐波响应分析中，使用线性摄动法来包括预应力效应。

螺栓调整变为零，施加电压为5V。

结果和讨论

具有线性扰动的预应力模态分析结果方法

在求解谐波响应分析之前，了解系统的频率内容非常重要，模态分析提供了这些有价值的信息。

在求解器输出中，z（纵向）方向上的参与因子列在模态分析的末尾，如下所示：

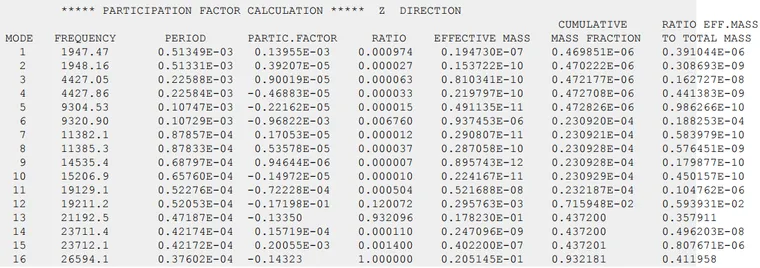
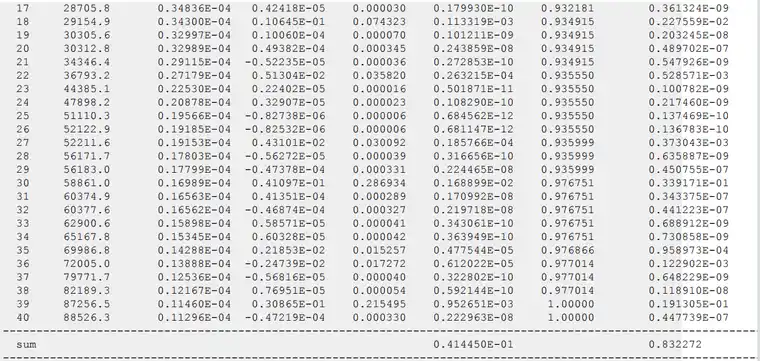
在z方向上具有高参与因子的模式是期望的纵向模态评估的候选。还应检查振型，以确定是否存在过度的横向运动，因为这些振型在换能器操作期间不应被激发。检查在这种情况下的结果，模态16、30和39是感兴趣的模态，如以下三个图所示。

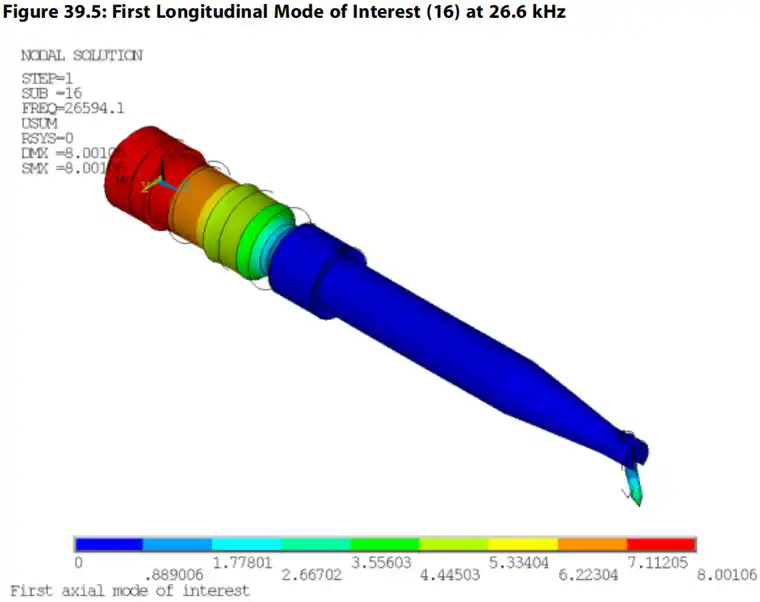
第二种感兴趣的模态将在随后的谐波响应分析中进行研究：

值得注意的是，如果换能器用于更高频率的应用，第三种感兴趣的模态为87.3kHz：

在所有模态下，与z方向相比，键合工具的尖端在x和y方向上几乎没有运动，这是进行正确的引线键合所必需的。此外，第二和第三模式的频率大致是第一模式的两倍和三倍，正如预期的那样。

预应力全谐波响应分析结果

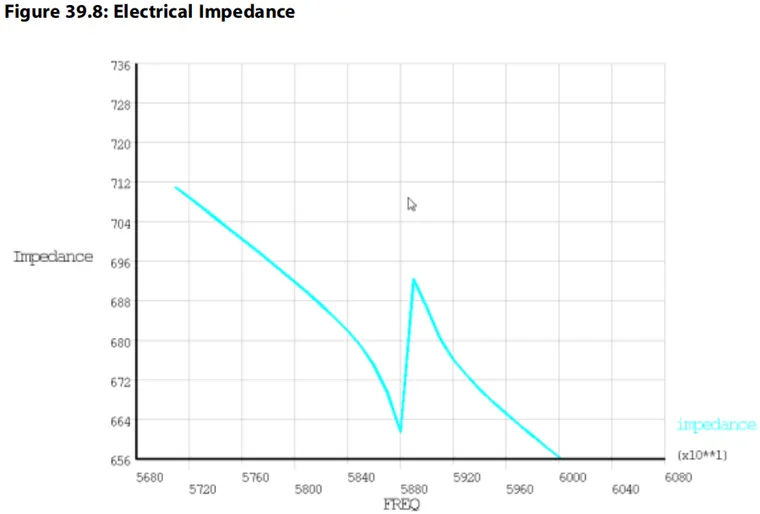
对于引线键合，传感器可以在50-60 kHz范围内工作。尽管模态分析确定感兴趣的第二纵向模式为58.9kHz，但需要确定实际振幅和阻抗值，因此进行谐波响应分析。

电压自由度的“反作用力”是电荷。在POST26时间历史后处理器（/POST26）中，在终端回溯电荷Q。因为电流和，则。该操作可通过CFACT和PROD命令执行，以基于电荷计算电流。阻抗计算和绘制如下：

尖端x、y和z位移直接在POST26中输出，并绘制如下：

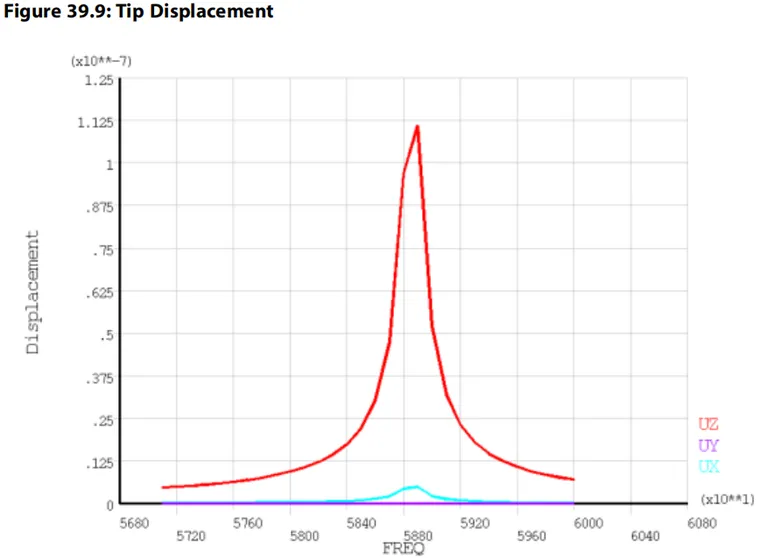
如图所示，横向运动（x和y）远小于纵向运动（z）。该施加电压的位移略大于0.1微米。

建议

要执行类似的分析，考虑以下提示和建议：

• 对于压电材料，确保极化方向（由单元坐标系定义）正确。无论选择哪个单元轴（x、y或z）作为极化方向，所有正交各向异性材料和压电常数都必须相应地定义。

• 对于压电常数，可以使用压电应力矩阵（[e]形式）或压电应变矩阵（[d]矩阵）。然而，如果使用压电应变矩阵，则必须通过TB,ANEL命令输入弹性特性。此外，IEEE标准列出了基于（x，y，z，yz，xz，xy）排序的系数，

• 而ANSYS输入需要（x，y，z，xy，yz，xz）排序。有关详细信息，请参见《耦合场分析指南》中的压电矩阵。通过调整网格单元大小以适应分析的频率范围，确保每个波长至少有六个单元用于感兴趣的最高频率。

• 在计算电阻抗时，根据“反作用力”电荷计算电流，如“预应力全谐波响应分析结果”所示。电压自由度受限的每个节点返回一部分“反应”电荷。然而，如果电压自由度是耦合的，则可以在主自由度（MDOF）下获得总的“反应”电荷，而不是对终端节点的所有“反作用”电荷求和。这种方法后处理简单得多，因为只需要查询来自单个节点（MDOF）的结果。

• 在谐波响应分析中，所有加载和边界条件均以正弦方式应用。因此，如果存在预紧力单元（PRETS179），则在分析的谐波响应部分将其调整限制为零。

• 对于线性扰动分析，使用基本线性静态分析中的RESCONTROL，linear命令生成多帧重启所需的文件（.Rnnn,.RDB,.ESAV）。线性扰动分析需要使用多帧重新启动文件，但除非发出RESCONTROL命令，否则不会为线性静态分析创建重新启动文件。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删