LS-DYNA动态破坏分析中的高级数值计算方法选择

背景介绍

破坏分析在数值模拟方面一直是难点问题。其困难之处在于不同的破坏模态（failure mode）有不同的物理基础和表现形式。目前没有统一的数值方法可以求解所有的破坏模式，所以就要求用户根据问题的本质和它的表现形式来选择一个合适的数值方法来解决问题。

为了抓住动态破坏过程，LS-DYNA针对各类破坏现象及其物理机理提供了多样化的先进数值计算方法。这些方法摒弃了传统有限元法中采用的单元删除法，能更准确的模拟材料在破坏过程中的变化。Smoothed Particle Galerkin (SPG)方法用于模拟延性材料在中低速材料加工，碰撞及高速碰撞过程中的损伤行为。Peridynamics方法面向脆性材料在中低速材料加工，碰撞过程中的各类裂纹，材料碎裂问题。eXtend FEM（XFEM）针对准脆性或延性板壳结构在受力状态下的裂纹扩展问题。Smoothed Particle Hydrodynamic（SPH）方法适用于各类固体材料在高速冲击状态下材料碎片化过程模拟。用户可以根据问题的材料特征及破坏表现形式选择合适的先进数值计算方法。

不同破坏模态的物理机制

LS-DYNA提供了各种各样的先进数值方法。针对failure分析，首先要了解不同的破坏模态具有不同的物理机制。例如金属等Ductile（延性）材料，其破坏模态表现为损伤。特征是在损伤的区域，强度会逐渐降低到零。对于此类问题其理论基础是损伤力学。此外，诸如玻璃、陶瓷、水泥或高强度钢等脆性或者准脆性材料，其破坏模态表现为裂纹。裂纹与损伤相比有不同的机理。在裂纹尖端存在有Stress singularity（应力的奇异性），理论上裂纹尖端的应力是无穷大的，但实际上并不存在无穷大的应力区，至少也是一个很高的应力区域，裂纹的力学理论是断裂力学。这两种破坏模态的表现形式不一样，例如在脆性的材料里主要表现为裂纹，单裂纹的扩展或多裂纹的扩展和交互作用，最终形成fragment，导致整个材料破碎。而对于延性材料来说，一个明显的特点是会存在一个很大的damage zone（损伤区域）。损伤区域里的材料强度会降低，且不会向远距离扩展。对于准脆性和延性材料，在一些冲击情况下也会发生裂纹扩展。

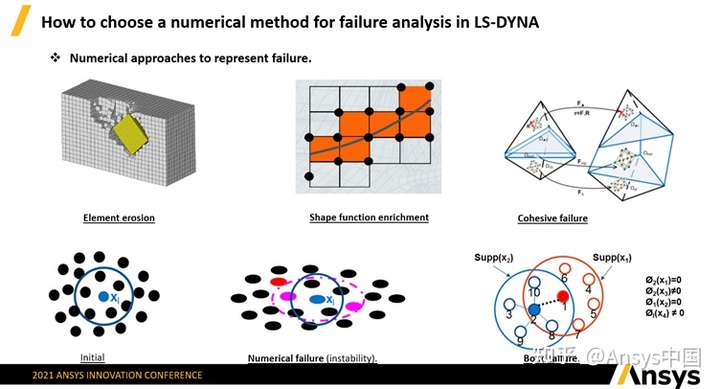
材料分离表达方式

这两种破坏模态都存在材料分离的现象。从数值方法角度来看，需要一个好的方式来表达材料的分离。一般有如下五种方式：

• Element erosion单元删除法。这是一种传统的方法，采用有限元法，材料一旦满足了一个准则以后就删除；
• 扩展有限元法XFEM。通过Shape function(形函数)在插值空间里面将材料分成两部分；
• Cohesive failure方法。即在两个固体单元之间增加一层有厚度或者没有厚度的Cohesive单元,如果增加的Cohesive单元破坏了，说明材料分开了；
• Numerical failure方法。例如SPH（上图中Initial图示），中心蓝点Xi和黑点相互关联，然而随着拉伸的进行，在搜索Xi单元的近邻时已无法找到。上图中Numerical Failure（instability）图示中，玫红色的点与蓝点之间的联系中断，此时可以认定材料损伤的发生，实际上是一种instability；
• Bond failure方法。LS-DYNA开发了一种特殊的方法，即Bond failure。该方法基于无网格法,可通过断掉图中红点及蓝点之间的联系来自由的表达材料的破坏和分离。

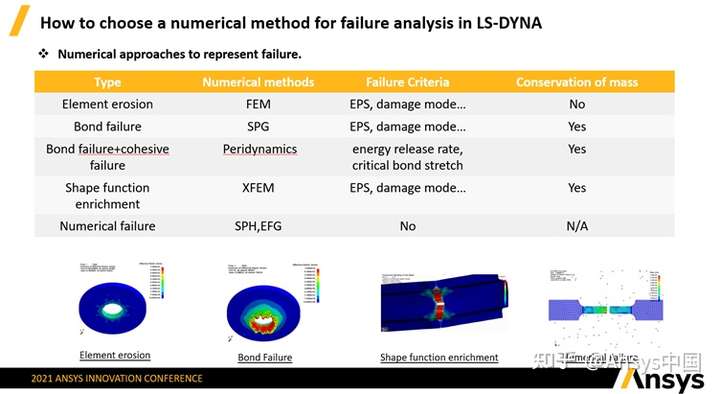
1）Element erosion单元删除的主要方法是Finite Element，破坏准则是EPS等效塑性应变或损伤模型（Damage mode），使用该方法时一旦删除单元，相应区域的mesh，质量和能动量（energy momentum）全部丢失；

2）Bond failure中，虽然物质点之间的联系中断了，但是相应的质量和动量都还在，该特性在材料加工过程中十分重要，会提供材料的额外强度支撑。该断裂方法在LS-DYNA中主要为SPG应用。SPG的bond破坏的准则是EPS等效塑性应变或损伤模型等，会保持质量守恒；

3）Shape function enrichment是扩展有限元XFEM方法，该方法需要跟踪裂纹界面，然后根据需要、通过形函数在插值空间表达裂纹。该方法也有等效塑性变或损伤模型作为破坏准则，并且可以满足质量守恒；

4）Numerical failure例如SPH无需Failure Criteria，这是由于在拉伸的过程中，当数值方法找不到两个点的关联而自动产生破坏，也不存在质量不守恒的问题。

LS-DYNA中提供的先进动态破坏数值方法

• SPG光滑粒子伽辽金法。该方法主要针对延性材料的破坏，模拟三维固体材料里的损伤，应用场景多为低中速的加工和高速的破坏；
• Peridynamics近场动力学方法。该方法主要处理脆性材料的多裂纹扩展及多裂纹扩展形成的脆片，面向三维的固体材料，应用场景多为中低速的加工或者是破坏；
• XFEM扩展有限元法。主要针对准脆性和延性材料的破坏，多应用于壳结构单裂纹扩展的中低速冲击问题；
• SPH光滑粒子流体动力学方法。该方法相对成熟，主要针对脆性和延性材料的破坏，多应用于高速冲击下三维固体材料的脆片化。SPH主要应用于流体分析，但由于是基于Lagrange的方法，所以也适用于固体分析，因为高速冲击下固体也会表现出流体的特性。

特征及案例介绍

* SPG方法

SPG方法是由LS-DYNA开发的真正意义上的无网格法。常规的无网格法需要背景网格来进行积分，在处理破坏时有一定局限性。而SPG法则使用节点积分，是真正意义上的稳定的无网格法。SPG可以十分便捷地与有限元part进行耦合，能够处理大变形等问题。可以使用LS-DYNA中的大部分材料模型，并且基于Physics based failure criteria进行破坏，其网格和损伤criteria的相关度很低，这是由于材料的网格粗细和材料损伤参数关联比较低，参数设置大小，对结果均没有太大影响。

视频中案例是两个典型的应用，左图是对某一金属板进行钻孔加工，之后再将其往上拉。可以看到钻孔过程中螺纹的形成，螺纹和螺栓之间会形成一个力，这是加工过程中所必需的力。在进行拉伸实验的时候，螺纹具有非常重要的支撑作用，如果用Element erosion，则无法形成螺纹。右图案例是高速冲击下混凝土的侵彻，可以看到在混凝土中心形成了一个damage zone（损伤区域），有材料喷出和spall fracture（裂纹扩展）现象。

* 近场动力学方法

主要针对脆性材料。与常规近场动力学相比，LS-DYNA近场动力学最大的区别是基于有限元实现的Peridynamic Model，其与LS-DYNA其他有限元部分的耦合十分简单，同时也是bond-based peridynamic。Bond-based peridynamic针对脆性材料，其损伤准则是能量释放率-断裂力学的概念之一，可以自动进行多裂纹的扩展、分叉、交互。由于是基于有限元进行实现的，其边界条件可以像有限元一样施加。

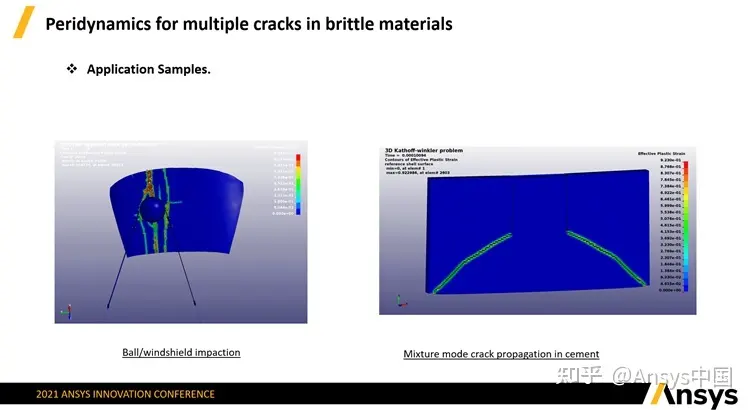
视频中左图案例是模拟汽车玻璃的碰撞，汽车玻璃上下两层玻璃中间夹了一层聚合物，典型三明治结构，从结果可以看到多裂纹的扩展和交互（复合型裂纹的扩展）。右图是混凝土的裂纹扩展模拟。

* 扩展有限元法

扩展有限元法，其裂纹表面是用Level Set水平集法来进行搜索、表现。目前扩展有限元多应用于Shell壳单元，是cell-by-cell的裂纹扩展，一次会切整个厚度，可应用于脆性和延性材料中，主要为高强度钢等材料。高强度钢在特定的冲击下会形成裂纹。LS-DYNA有多个破坏准则可以选择，常规数值方法会有很强的网格的相关性，为了消除这类网格敏感性，LS-DYNA扩展有限元法开发了一种特殊的数值方法处理-Strain regularization，其可以用不同的网格大小得到相对收敛的结果。

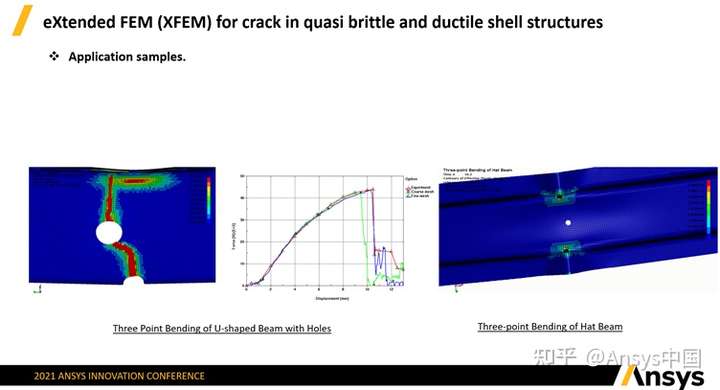
视频中左图是一个U-shaped高强度钢的梁结构承压模拟，中间的孔是为了触发裂纹而设置，使裂纹延展到孔所在的区域。上右图是一个HAT-shape类似帽子形状的梁结构，在该梁结构上施加一定的压力，可以看到两个裂纹在两边同时扩展，与脆性材料不同，这两个单独的裂纹没有交互，而脆性材料在裂纹扩展的时候各种各样的裂纹会互相交互影响。

* SPH流体动力学方法

SPH流体动力学方法，计算速度相对快，主要是对流体和固体进行计算。因为SPH是基于Lagrange的，其流固耦合计算十分简单，SPH的热固耦合亦非常优秀，大部分的材料模型都能使用。

如视频中左图所示，鸟撞发动机叶片是一种典型的SPH的应用。右图是一种结构撞击问题，SPH可能会存在数值不稳定的问题。为了解决这个问题，LS-DYNA开发了Adaptive SPH（自适应SPH）和高阶的Eulerian kernel来解决数值不稳定的问题。右图可以看到Lagrangian kernel和Eulerian kernel可得到相同的结果，不存在数值失效的问题。

总结

在进行破坏模拟的时候，一定要了解其物理失效机制，抓住问题的本质。每一种数值方法均有各自的优缺点，需找到准确的方法。LS-DYNA 提供了各种各样的先进的数值方法（除了以上所介绍的几种方法之外，以往还有自适应四面体单元、EFG、SALE、Cohesive、bonded DEM等），每一种方法都针对特定的应用。LS-DYNA 提供的先进数值方法，同时能很好地和软件中其他的数值方法进行耦合。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删